Beam Squinting Effects in Super Wideband Communication Systems

Beam squint, the frequency-dependent shift of the main beam, poses a major challenge for wideband antenna arrays. This paper focuses on the beam squint effects in super wideband (SW) systems, where high mutual coupling (MC) effects are present. These high MC effects complicate beamforming (BF) by creating frequency-dependent phase relationships that invalidate conventional approaches. To accurately model MC effects, this paper uses a circuit-theoretic framework for tightly coupled SW uniform linear arrays (ULAs). We derive closed-form expressions for the average received signal-to-noise ratio (SNR) with BF in conventional half-wavelength spaced, weakly coupled arrays and validate them. Extending our analysis to tightly coupled SW arrays, we demonstrate that, in contrast to conventional weakly coupled arrays, the effective true time delays exhibit a nonlinear dependence on frequency due to coupling-induced phase shifts. A comparative analysis reveals that strong MC in SW arrays significantly reduces squint in phase-controlled BF, extending the usable bandwidth considerably.

MCAnalysis: An Open-Source Package for Preprocessing, Modelling, and Visualisation of Menstrual Cycle Effects in Digital Health Data

The menstrual cycle influences numerous physiological and psychological outcomes, yet standardised, open-source statistical methods for quantifying these cyclic effects remain lacking. We developed mcanalysis, an open-source package in R and Python implementing a Fourier-basis generalised additive model (GAM) for menstrual cycle research. The package provides a complete pipeline: processing period dates, labelling cycle days relative to menstruation onset, filtering physiologically plausible cycles, normalising outcomes to individual means, fitting cyclic GAMs with bootstrap confidence intervals, and identifying turning points to generate phase-specific linear trend estimates. We demonstrate the package on 15 wearable and self-reported outcomes using data from the Juli chronic health management application (N = 2,816 users). Nine of 15 outcomes showed evidence of association with the menstrual cycle (p < 0.05), spanning physiological (HRV p < 0.001, oxygen saturation p = 0.002), sleep (p = 0.003), symptom (migraine p < 0.001, headache p = 0.005), mood (EMA mood p = 0.024, PHQ-8 lack of energy p = 0.008, mania p = 0.041), and activity (hours outside p = 0.019) domains. No tested confounders were significantly associated with cycle-normalised outcomes. mcanalysis provides a standardised, reproducible approach to menstrual cycle analysis for users at all levels of statistical expertise. The package is freely available at https://github.com/kyradelray/mcanalysis, with a no-code web interface at https://kyradelray.shinyapps.io/mcanalysis/.

Rician Channel Modelling for Super Wideband MIMO Communications

Recent developments in Multiple-Input-Multiple-Output (MIMO) technology include packing a large number of antenna elements in a compact array to access the bandwidth benefits provided by higher mutual coupling (MC). The resulting super-wideband (SW) systems require a circuit-theoretic framework to handle the MC and channel models which span extremely large bands. Hence, in this paper, we make two key contributions. First, we develop a physically-consistent Rician channel model for use with SW systems. Secondly, we express the circuit-theoretic models in terms of a standard MIMO model, so that insights into the effects of antenna layouts, MC, and bandwidth can be made using standard communication theory. For example, we show the bandwidth widening resulting from the new channel model. In addition, we show that MC distorts line-of-sight paths which has beamforming implications. We also highlight the interaction between spatial correlation and MC and show that tight coupling reduces spatial correlations at low frequencies.

A fast score-based search algorithm for maximal ancestral graphs using entropy

\emph{Maximal ancestral graph} (MAGs) is a class of graphical model that extend the famous \emph{directed acyclic graph} in the presence of latent confounders. Most score-based approaches to learn the unknown MAG from empirical data rely on BIC score which suffers from instability and heavy computations. We propose to use the framework of imsets \citep{studeny2006probabilistic} to score MAGs using empirical entropy estimation and the newly proposed \emph{refined Markov property} \citep{hu2023towards}. Our graphical search procedure is similar to \citet{claassen2022greedy} but improved from our theoretical results. We show that our search algorithm is polynomial in number of nodes by restricting degree, maximal head size and number of discriminating paths. In simulated experiment, our algorithm shows superior performance compared to other state of art MAG learning algorithms.

Selection, Ignorability and Challenges With Causal Fairness

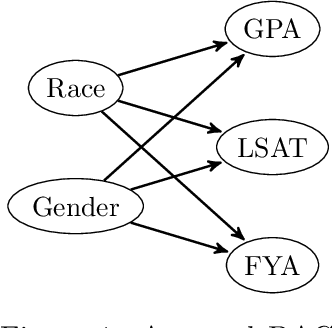
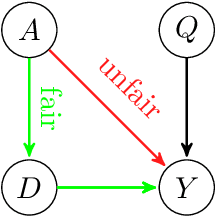
In this paper we look at popular fairness methods that use causal counterfactuals. These methods capture the intuitive notion that a prediction is fair if it coincides with the prediction that would have been made if someone's race, gender or religion were counterfactually different. In order to achieve this, we must have causal models that are able to capture what someone would be like if we were to counterfactually change these traits. However, we argue that any model that can do this must lie outside the particularly well behaved class that is commonly considered in the fairness literature. This is because in fairness settings, models in this class entail a particularly strong causal assumption, normally only seen in a randomised controlled trial. We argue that in general this is unlikely to hold. Furthermore, we show in many cases it can be explicitly rejected due to the fact that samples are selected from a wider population. We show this creates difficulties for counterfactual fairness as well as for the application of more general causal fairness methods.

Combined Radar and Communications with Phase-Modulated Frequency Permutations

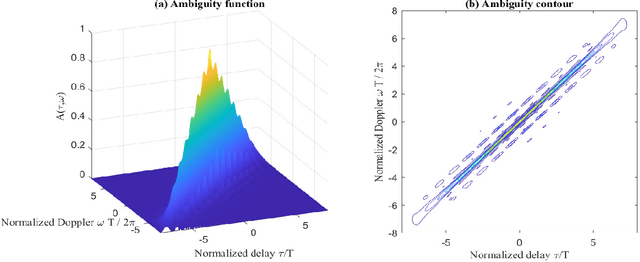
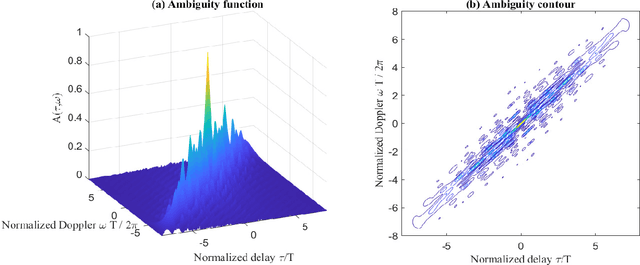
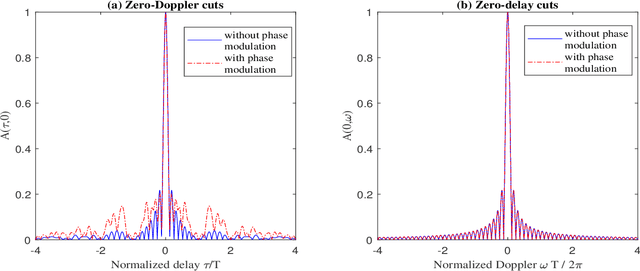
This paper focuses on the combined radar and communications problem and conducts a thorough analytical investigation on the effect of phase and frequency change on the communication and sensing functionality. First, we consider the classical stepped frequency radar waveform and modulate data using M-ary phase shift keying (MPSK). Two important analytical tools in radar waveform design, namely the ambiguity function (AF) and the Fisher information matrix (FIM) are derived, based on which, we make the important conclusion that MPSK modulation has a negligible effect on radar local accuracy. Next, we extend the analysis to incorporate frequency permutations and propose a new signalling scheme in which the mapping between incoming data and waveforms is performed based on an efficient combinatorial transform called the Lehmer code. We also provide an efficient communications receiver based on the Hungarian algorithm. From the communications perspective, we consider the optimal maximum likelihood (ML) detector and derive the union bound and nearest neighbour approximation on the block error probability. From the radar sensing perspective, we discuss the broader structure of the waveform based on the AF derivation and quantify the radar local accuracy based on the FIM.

Frequency Permutations for Joint Radar and Communications

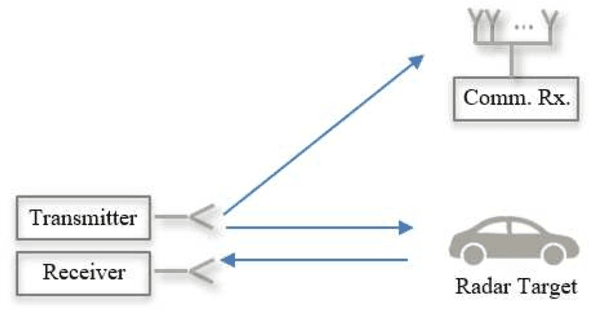
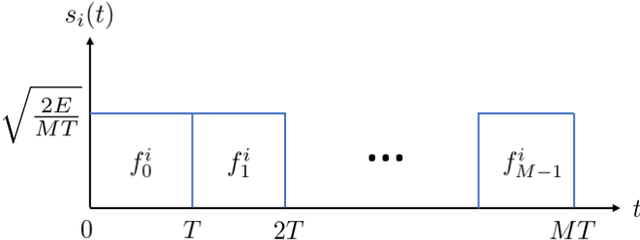
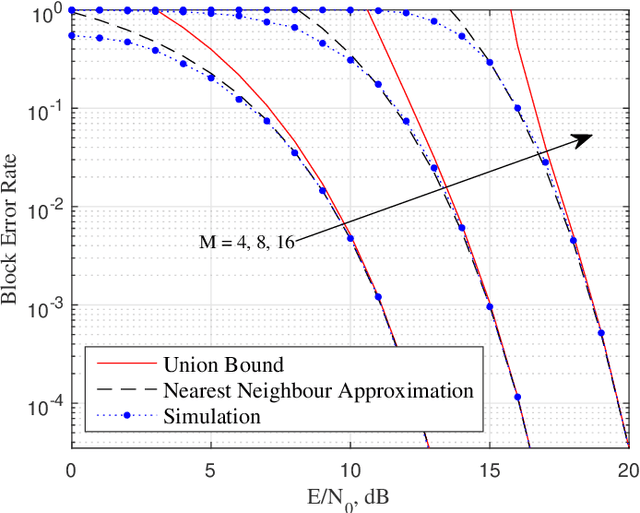
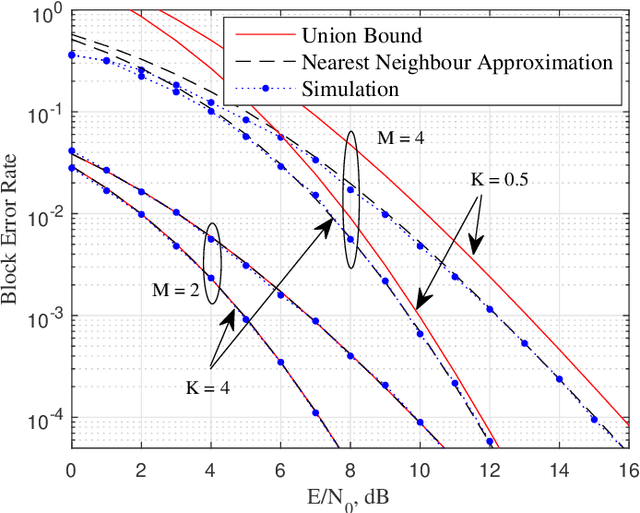
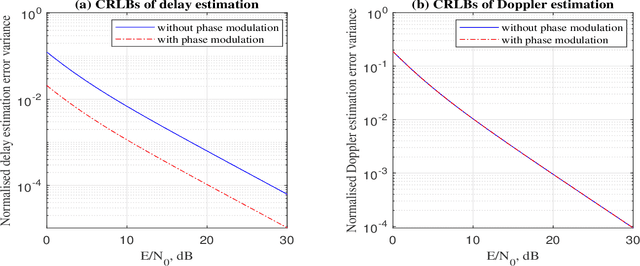
This paper presents a new joint radar and communication technique based on the classical stepped frequency radar waveform. The randomization in the waveform, which is achieved by using permutations of the sequence of frequency tones, is utilized for data transmission. A new signaling scheme is proposed in which the mapping between incoming data and waveforms is performed based on an efficient combinatorial transform called the Lehmer code. Considering the optimum maximum likelihood (ML) detection, the union bound and the nearest neighbour approximation on the communication block error probability is derived for communication in an additive white Gaussian noise (AWGN) channel. The results are further extended to incorporate the Rician fading channel model, of which the Rayleigh fading channel model is presented as a special case. Furthermore, an efficient communication receiver implementation is discussed based on the Hungarian algorithm which achieves optimum performance with much less operational complexity when compared to an exhaustive search. From the radar perspective, two key analytical tools, namely, the ambiguity function (AF) and the Fisher information matrix are derived. Furthermore, accurate approximations to the Cramer-Rao lower bounds (CRLBs) on the delay and Doppler estimation errors are derived based on which the range and velocity estimation accuracy of the waveform is analysed. Numerical examples are used to highlight the accuracy of the analysis and to illustrate the performance of the proposed waveform.

Inverse Cognitive Radar -- A Revealed Preferences Approach

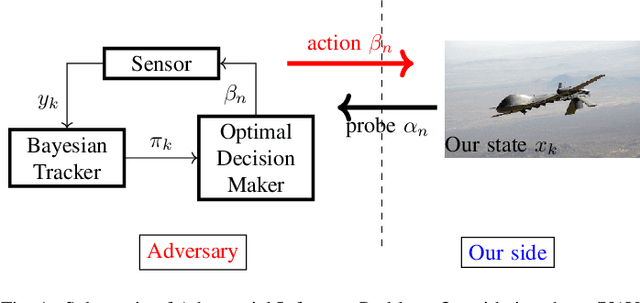
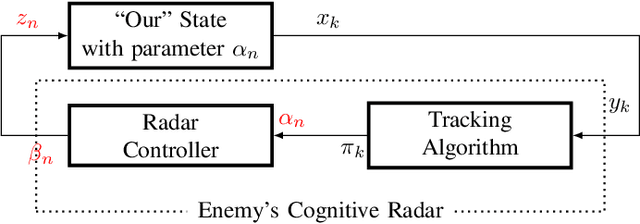
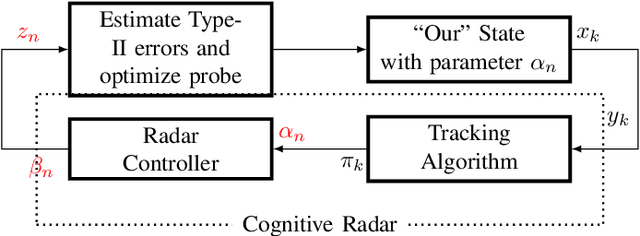
We consider an adversarial signal processing problem involving "us" versus an "enemy" cognitive radar. The enemy's cognitive radar observes our state in noise; uses a tracker to update its posterior distribution of our state and then chooses an action based on this posterior. Given knowledge of "our" state and the observed sequence of actions taken by the enemy's radar, we consider three problems: (i) Are the enemy radar's actions consistent with optimizing a monotone utility function (i.e., is the cognitive radar behavior rational in an economics sense). If so how can we estimate the adversary's cognitive radar's utility function that is consistent with its actions. (ii) How to construct a statistical detection test for utility maximization when we observe the enemy radar's actions in noise? (iii) How can we optimally probe the enemy's radar by choosing our state to minimize the Type 2 error of detecting if the radar is deploying an economic rational strategy, subject to a constraint on the Type 1 detection error? "Our" state can be viewed as a probe signal which causes the enemy's radar to act; so choosing the optimal state sequence is an input design problem. The main analysis framework used in this paper is that of revealed preferences from microeconomics.

Causal Inference through a Witness Protection Program

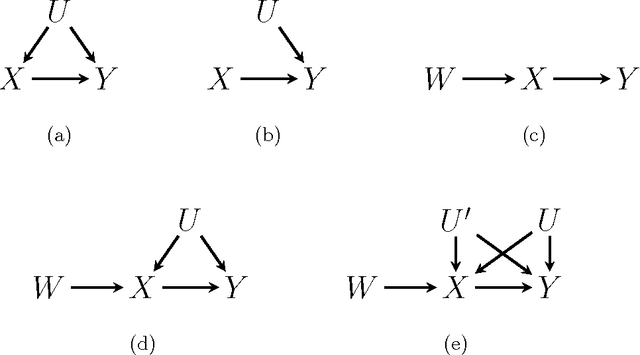
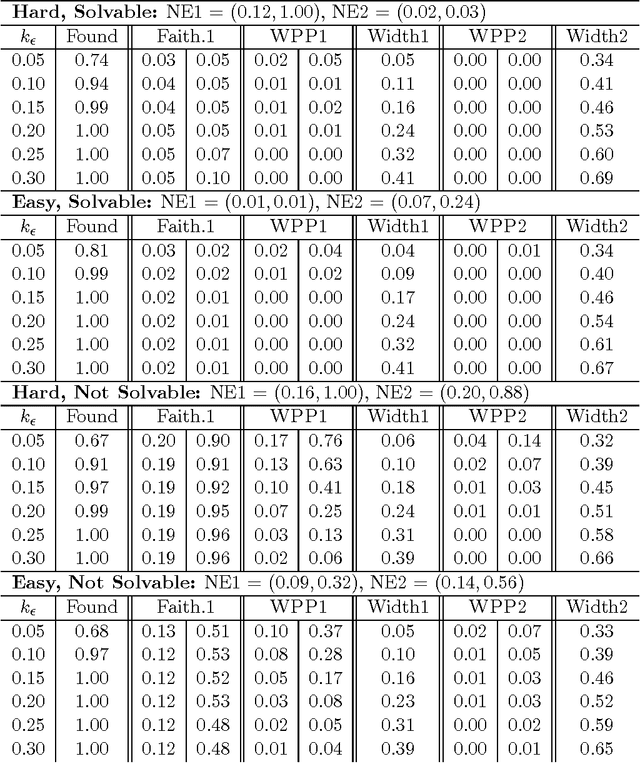
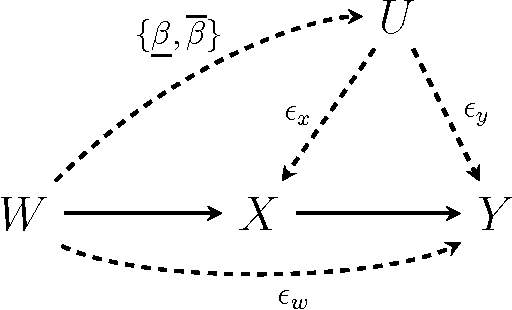
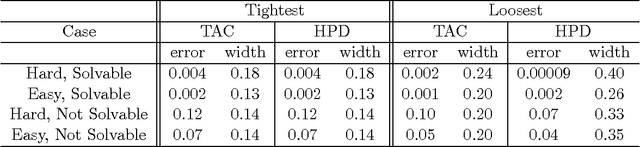
One of the most fundamental problems in causal inference is the estimation of a causal effect when variables are confounded. This is difficult in an observational study, because one has no direct evidence that all confounders have been adjusted for. We introduce a novel approach for estimating causal effects that exploits observational conditional independencies to suggest "weak" paths in a unknown causal graph. The widely used faithfulness condition of Spirtes et al. is relaxed to allow for varying degrees of "path cancellations" that imply conditional independencies but do not rule out the existence of confounding causal paths. The outcome is a posterior distribution over bounds on the average causal effect via a linear programming approach and Bayesian inference. We claim this approach should be used in regular practice along with other default tools in observational studies.

Parameter and Structure Learning in Nested Markov Models

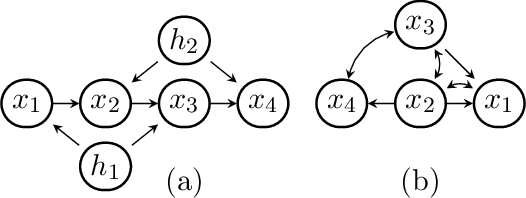
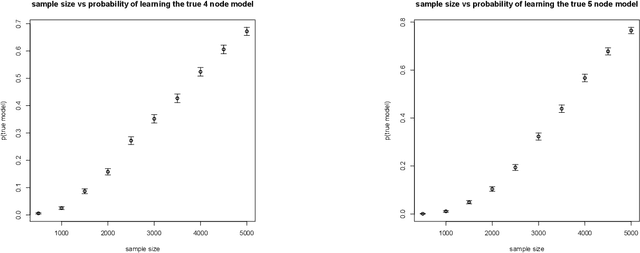
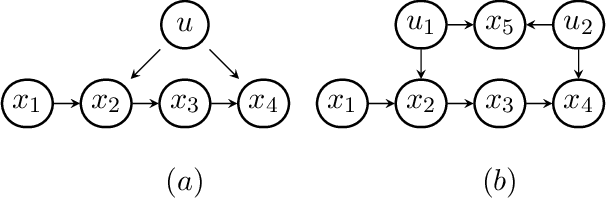
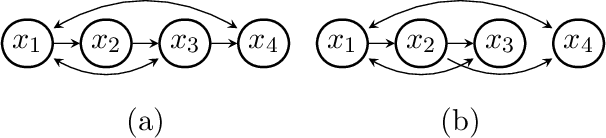
The constraints arising from DAG models with latent variables can be naturally represented by means of acyclic directed mixed graphs (ADMGs). Such graphs contain directed and bidirected arrows, and contain no directed cycles. DAGs with latent variables imply independence constraints in the distribution resulting from a 'fixing' operation, in which a joint distribution is divided by a conditional. This operation generalizes marginalizing and conditioning. Some of these constraints correspond to identifiable 'dormant' independence constraints, with the well known 'Verma constraint' as one example. Recently, models defined by a set of the constraints arising after fixing from a DAG with latents, were characterized via a recursive factorization and a nested Markov property. In addition, a parameterization was given in the discrete case. In this paper we use this parameterization to describe a parameter fitting algorithm, and a search and score structure learning algorithm for these nested Markov models. We apply our algorithms to a variety of datasets.