Zero Inflation as a Missing Data Problem: a Proxy-based Approach

A common type of zero-inflated data has certain true values incorrectly replaced by zeros due to data recording conventions (rare outcomes assumed to be absent) or details of data recording equipment (e.g. artificial zeros in gene expression data). Existing methods for zero-inflated data either fit the observed data likelihood via parametric mixture models that explicitly represent excess zeros, or aim to replace excess zeros by imputed values. If the goal of the analysis relies on knowing true data realizations, a particular challenge with zero-inflated data is identifiability, since it is difficult to correctly determine which observed zeros are real and which are inflated. This paper views zero-inflated data as a general type of missing data problem, where the observability indicator for a potentially censored variable is itself unobserved whenever a zero is recorded. We show that, without additional assumptions, target parameters involving a zero-inflated variable are not identified. However, if a proxy of the missingness indicator is observed, a modification of the effect restoration approach of Kuroki and Pearl allows identification and estimation, given the proxy-indicator relationship is known. If this relationship is unknown, our approach yields a partial identification strategy for sensitivity analysis. Specifically, we show that only certain proxy-indicator relationships are compatible with the observed data distribution. We give an analytic bound for this relationship in cases with a categorical outcome, which is sharp in certain models. For more complex cases, sharp numerical bounds may be computed using methods in Duarte et al.[2023]. We illustrate our method via simulation studies and a data application on central line-associated bloodstream infections (CLABSIs).

Evaluation of Active Feature Acquisition Methods for Static Feature Settings

Active feature acquisition (AFA) agents, crucial in domains like healthcare where acquiring features is often costly or harmful, determine the optimal set of features for a subsequent classification task. As deploying an AFA agent introduces a shift in missingness distribution, it's vital to assess its expected performance at deployment using retrospective data. In a companion paper, we introduce a semi-offline reinforcement learning (RL) framework for active feature acquisition performance evaluation (AFAPE) where features are assumed to be time-dependent. Here, we study and extend the AFAPE problem to cover static feature settings, where features are time-invariant, and hence provide more flexibility to the AFA agents in deciding the order of the acquisitions. In this static feature setting, we derive and adapt new inverse probability weighting (IPW), direct method (DM), and double reinforcement learning (DRL) estimators within the semi-offline RL framework. These estimators can be applied when the missingness in the retrospective dataset follows a missing-at-random (MAR) pattern. They also can be applied to missing-not-at-random (MNAR) patterns in conjunction with appropriate existing missing data techniques. We illustrate the improved data efficiency offered by the semi-offline RL estimators in synthetic and real-world data experiments under synthetic MAR and MNAR missingness.

Evaluation of Active Feature Acquisition Methods for Time-varying Feature Settings

Machine learning methods often assume input features are available at no cost. However, in domains like healthcare, where acquiring features could be expensive or harmful, it is necessary to balance a feature's acquisition cost against its predictive value. The task of training an AI agent to decide which features to acquire is called active feature acquisition (AFA). By deploying an AFA agent, we effectively alter the acquisition strategy and trigger a distribution shift. To safely deploy AFA agents under this distribution shift, we present the problem of active feature acquisition performance evaluation (AFAPE). We examine AFAPE under i) a no direct effect (NDE) assumption, stating that acquisitions don't affect the underlying feature values; and ii) a no unobserved confounding (NUC) assumption, stating that retrospective feature acquisition decisions were only based on observed features. We show that one can apply offline reinforcement learning under the NUC assumption and missing data methods under the NDE assumption. When NUC and NDE hold, we propose a novel semi-offline reinforcement learning framework, which requires a weaker positivity assumption and yields more data-efficient estimators. We introduce three novel estimators: a direct method (DM), an inverse probability weighting (IPW), and a double reinforcement learning (DRL) estimator.

Identification and Estimation for Nonignorable Missing Data: A Data Fusion Approach

We consider the task of identifying and estimating a parameter of interest in settings where data is missing not at random (MNAR). In general, such parameters are not identified without strong assumptions on the missing data model. In this paper, we take an alternative approach and introduce a method inspired by data fusion, where information in an MNAR dataset is augmented by information in an auxiliary dataset subject to missingness at random (MAR). We show that even if the parameter of interest cannot be identified given either dataset alone, it can be identified given pooled data, under two complementary sets of assumptions. We derive an inverse probability weighted (IPW) estimator for identified parameters, and evaluate the performance of our estimation strategies via simulation studies.

An Introduction to Causal Inference Methods for Observational Human-Robot Interaction Research

Quantitative methods in Human-Robot Interaction (HRI) research have primarily relied upon randomized, controlled experiments in laboratory settings. However, such experiments are not always feasible when external validity, ethical constraints, and ease of data collection are of concern. Furthermore, as consumer robots become increasingly available, increasing amounts of real-world data will be available to HRI researchers, which prompts the need for quantative approaches tailored to the analysis of observational data. In this article, we present an alternate approach towards quantitative research for HRI researchers using methods from causal inference that can enable researchers to identify causal relationships in observational settings where randomized, controlled experiments cannot be run. We highlight different scenarios that HRI research with consumer household robots may involve to contextualize how methods from causal inference can be applied to observational HRI research. We then provide a tutorial summarizing key concepts from causal inference using a graphical model perspective and link to code examples throughout the article, which are available at https://gitlab.com/causal/causal_hri. Our work paves the way for further discussion on new approaches towards observational HRI research while providing a starting point for HRI researchers to add causal inference techniques to their analytical toolbox.

When does the ID algorithm fail?

The ID algorithm solves the problem of identification of interventional distributions of the form p(Y | do(a)) in graphical causal models, and has been formulated in a number of ways [12, 9, 6]. The ID algorithm is sound (outputs the correct functional of the observed data distribution whenever p(Y | do(a)) is identified in the causal model represented by the input graph), and complete (explicitly flags as a failure any input p(Y | do(a)) whenever this distribution is not identified in the causal model represented by the input graph). The reference [9] provides a result, the so called "hedge criterion" (Corollary 3), which aims to give a graphical characterization of situations when the ID algorithm fails to identify its input in terms of a structure in the input graph called the hedge. While the ID algorithm is, indeed, a sound and complete algorithm, and the hedge structure does arise whenever the input distribution is not identified, Corollary 3 presented in [9] is incorrect as stated. In this note, I outline the modern presentation of the ID algorithm, discuss a simple counterexample to Corollary 3, and provide a number of graphical characterizations of the ID algorithm failing to identify its input distribution.

Partial Identification of Causal Effects Using Proxy Variables

Proximal causal inference is a recently proposed framework for evaluating the causal effect of a treatment on an outcome variable in the presence of unmeasured confounding (Miao et al., 2018; Tchetgen Tchetgen et al., 2020). For nonparametric point identification of causal effects, the framework leverages a pair of so-called treatment and outcome confounding proxy variables, in order to identify a bridge function that matches the dependence of potential outcomes or treatment variables on the hidden factors to corresponding functions of observed proxies. Unique identification of a causal effect via a bridge function crucially requires that proxies are sufficiently relevant for hidden factors, a requirement that has previously been formalized as a completeness condition. However, completeness is well-known not to be empirically testable, and although a bridge function may be well-defined in a given setting, lack of completeness, sometimes manifested by availability of a single type of proxy, may severely limit prospects for identification of a bridge function and thus a causal effect; therefore, potentially restricting the application of the proximal causal framework. In this paper, we propose partial identification methods that do not require completeness and obviate the need for identification of a bridge function. That is, we establish that proxies of unobserved confounders can be leveraged to obtain bounds on the causal effect of the treatment on the outcome even if available information does not suffice to identify either a bridge function or a corresponding causal effect of interest. We further establish analogous partial identification results in related settings where identification hinges upon hidden mediators for which proxies are available, however such proxies are not sufficiently rich for point identification of a bridge function or a corresponding causal effect of interest.

Causal Discovery in Linear Latent Variable Models Subject to Measurement Error

We focus on causal discovery in the presence of measurement error in linear systems where the mixing matrix, i.e., the matrix indicating the independent exogenous noise terms pertaining to the observed variables, is identified up to permutation and scaling of the columns. We demonstrate a somewhat surprising connection between this problem and causal discovery in the presence of unobserved parentless causes, in the sense that there is a mapping, given by the mixing matrix, between the underlying models to be inferred in these problems. Consequently, any identifiability result based on the mixing matrix for one model translates to an identifiability result for the other model. We characterize to what extent the causal models can be identified under a two-part faithfulness assumption. Under only the first part of the assumption (corresponding to the conventional definition of faithfulness), the structure can be learned up to the causal ordering among an ordered grouping of the variables but not all the edges across the groups can be identified. We further show that if both parts of the faithfulness assumption are imposed, the structure can be learned up to a more refined ordered grouping. As a result of this refinement, for the latent variable model with unobserved parentless causes, the structure can be identified. Based on our theoretical results, we propose causal structure learning methods for both models, and evaluate their performance on synthetic data.

Causal and counterfactual views of missing data models

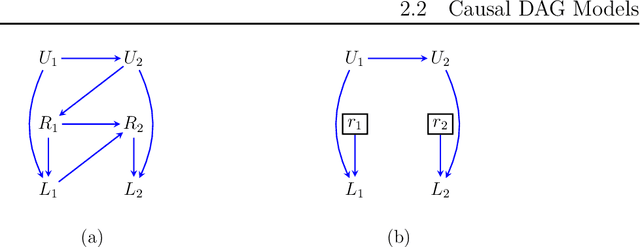
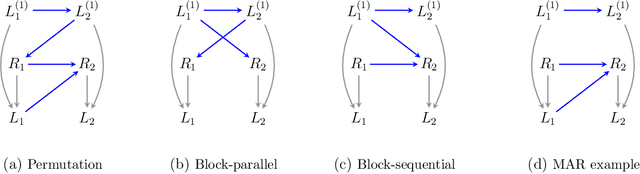
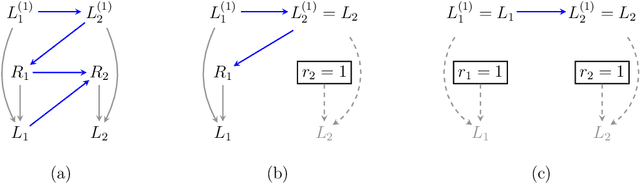
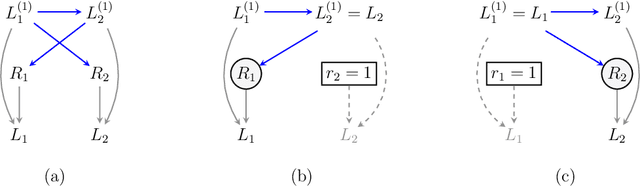
It is often said that the fundamental problem of causal inference is a missing data problem -- the comparison of responses to two hypothetical treatment assignments is made difficult because for every experimental unit only one potential response is observed. In this paper, we consider the implications of the converse view: that missing data problems are a form of causal inference. We make explicit how the missing data problem of recovering the complete data law from the observed law can be viewed as identification of a joint distribution over counterfactual variables corresponding to values had we (possibly contrary to fact) been able to observe them. Drawing analogies with causal inference, we show how identification assumptions in missing data can be encoded in terms of graphical models defined over counterfactual and observed variables. We review recent results in missing data identification from this viewpoint. In doing so, we note interesting similarities and differences between missing data and causal identification theories.

Combining Experimental and Observational Data for Identification of Long-Term Causal Effects

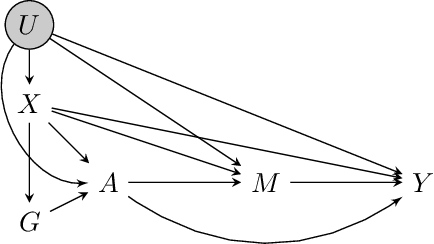
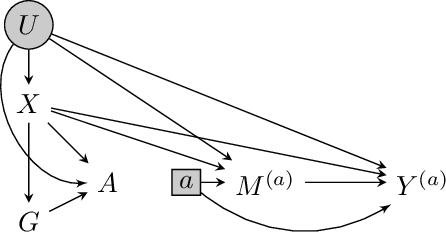
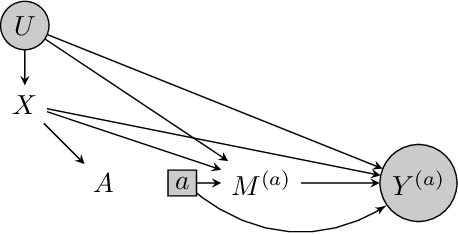
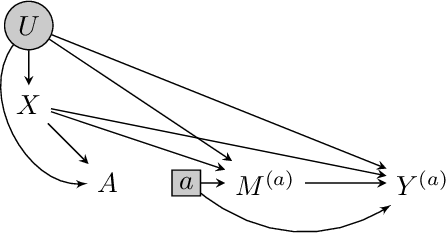
We consider the task of estimating the causal effect of a treatment variable on a long-term outcome variable using data from an observational domain and an experimental domain. The observational data is assumed to be confounded and hence without further assumptions, this dataset alone cannot be used for causal inference. Also, only a short-term version of the primary outcome variable of interest is observed in the experimental data, and hence, this dataset alone cannot be used for causal inference either. In a recent work, Athey et al. (2020) proposed a method for systematically combining such data for identifying the downstream causal effect in view. Their approach is based on the assumptions of internal and external validity of the experimental data, and an extra novel assumption called latent unconfoundedness. In this paper, we first review their proposed approach and discuss the latent unconfoundedness assumption. Then we propose two alternative approaches for data fusion for the purpose of estimating average treatment effect as well as the effect of treatment on the treated. Our first proposed approach is based on assuming equi-confounding bias for the short-term and long-term outcomes. Our second proposed approach is based on the proximal causal inference framework, in which we assume the existence of an extra variable in the system which is a proxy of the latent confounder of the treatment-outcome relation.