Deeper Interpretability of Deep Networks

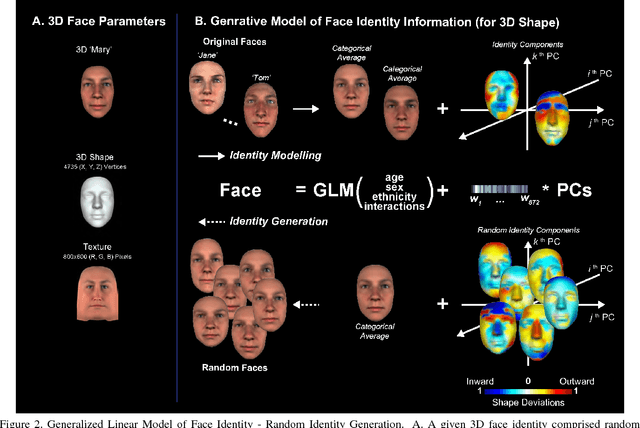
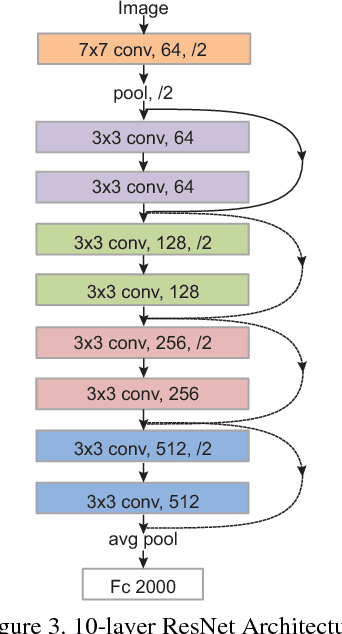
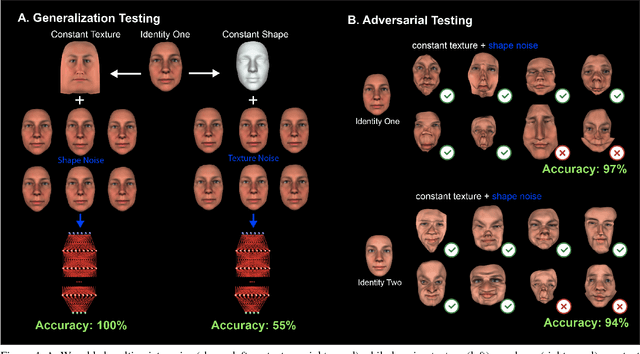
Deep Convolutional Neural Networks (CNNs) have been one of the most influential recent developments in computer vision, particularly for categorization. There is an increasing demand for explainable AI as these systems are deployed in the real world. However, understanding the information represented and processed in CNNs remains in most cases challenging. Within this paper, we explore the use of new information theoretic techniques developed in the field of neuroscience to enable novel understanding of how a CNN represents information. We trained a 10-layer ResNet architecture to identify 2,000 face identities from 26M images generated using a rigorously controlled 3D face rendering model that produced variations of intrinsic (i.e. face morphology, gender, age, expression and ethnicity) and extrinsic factors (i.e. 3D pose, illumination, scale and 2D translation). With our methodology, we demonstrate that unlike human's network overgeneralizes face identities even with extreme changes of face shape, but it is more sensitive to changes of texture. To understand the processing of information underlying these counterintuitive properties, we visualize the features of shape and texture that the network processes to identify faces. Then, we shed a light into the inner workings of the black box and reveal how hidden layers represent these features and whether the representations are invariant to pose. We hope that our methodology will provide an additional valuable tool for interpretability of CNNs.

Exact partial information decompositions for Gaussian systems based on dependency constraints

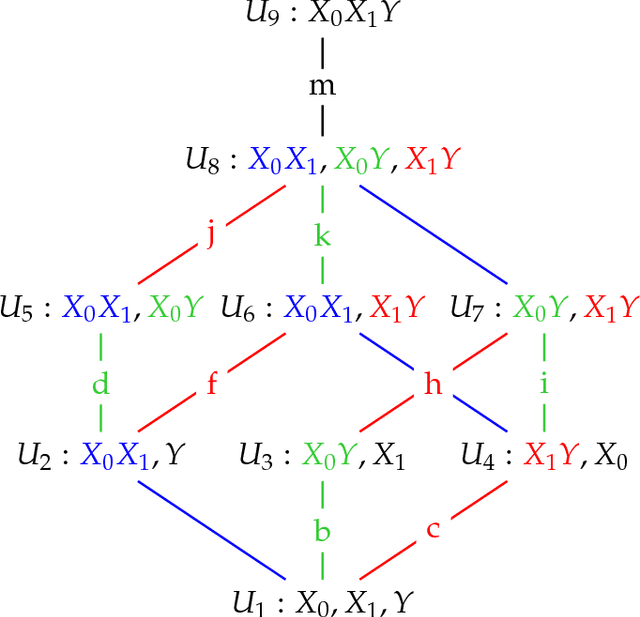
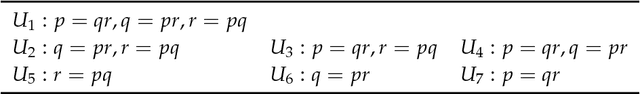
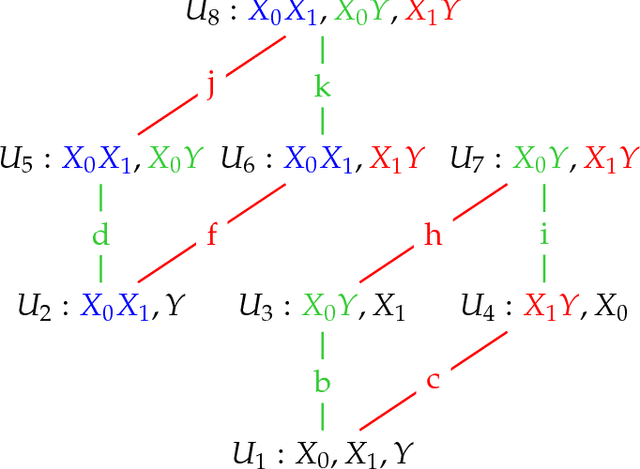
The Partial Information Decomposition (PID) [arXiv:1004.2515] provides a theoretical framework to characterize and quantify the structure of multivariate information sharing. A new method (Idep) has recently been proposed for computing a two-predictor PID over discrete spaces. [arXiv:1709.06653] A lattice of maximum entropy probability models is constructed based on marginal dependency constraints, and the unique information that a particular predictor has about the target is defined as the minimum increase in joint predictor-target mutual information when that particular predictor-target marginal dependency is constrained. Here, we apply the Idep approach to Gaussian systems, for which the marginally constrained maximum entropy models are Gaussian graphical models. Closed form solutions for the Idep PID are derived for both univariate and multivariate Gaussian systems. Numerical and graphical illustrations are provided, together with practical and theoretical comparisons of the Idep PID with the minimum mutual information PID (Immi). [arXiv:1411.2832] In particular, it is proved that the Immi method generally produces larger estimates of redundancy and synergy than does the Idep method. In discussion of the practical examples, the PIDs are complemented by the use of deviance tests for the comparison of Gaussian graphical models.