DatBench: Discriminative, Faithful, and Efficient VLM Evaluations

Empirical evaluation serves as the primary compass guiding research progress in foundation models. Despite a large body of work focused on training frontier vision-language models (VLMs), approaches to their evaluation remain nascent. To guide their maturation, we propose three desiderata that evaluations should satisfy: (1) faithfulness to the modality and application, (2) discriminability between models of varying quality, and (3) efficiency in compute. Through this lens, we identify critical failure modes that violate faithfulness and discriminability, misrepresenting model capabilities: (i) multiple-choice formats reward guessing, poorly reflect downstream use cases, and saturate early as models improve; (ii) blindly solvable questions, which can be answered without images, constitute up to 70% of some evaluations; and (iii) mislabeled or ambiguous samples compromise up to 42% of examples in certain datasets. Regarding efficiency, the computational burden of evaluating frontier models has become prohibitive: by some accounts, nearly 20% of development compute is devoted to evaluation alone. Rather than discarding existing benchmarks, we curate them via transformation and filtering to maximize fidelity and discriminability. We find that converting multiple-choice questions to generative tasks reveals sharp capability drops of up to 35%. In addition, filtering blindly solvable and mislabeled samples improves discriminative power while simultaneously reducing computational cost. We release DatBench-Full, a cleaned evaluation suite of 33 datasets spanning nine VLM capabilities, and DatBench, a discriminative subset that achieves 13x average speedup (up to 50x) while closely matching the discriminative power of the original datasets. Our work outlines a path toward evaluation practices that are both rigorous and sustainable as VLMs continue to scale.

Luxical: High-Speed Lexical-Dense Text Embeddings

Frontier language model quality increasingly hinges on our ability to organize web-scale text corpora for training. Today's dominant tools trade off speed and flexibility: lexical classifiers (e.g., FastText) are fast but limited to producing classification output scores, while the vector-valued outputs of transformer text embedding models flexibly support numerous workflows (e.g., clustering, classification, and retrieval) but are computationally expensive to produce. We introduce Luxical, a library for high-speed "lexical-dense" text embeddings that aims to recover the best properties of both approaches for web-scale text organization. Luxical combines sparse TF--IDF features, a small ReLU network, and a knowledge distillation training regimen to approximate large transformer embedding models at a fraction of their operational cost. In this technical report, we describe the Luxical architecture and training objective and evaluate a concrete Luxical model in two disparate applications: a targeted webcrawl document retrieval test and an end-to-end language model data curation task grounded in text classification. In these tasks we demonstrate speedups ranging from 3x to 100x over varying-sized neural baselines, and comparable to FastText model inference during the data curation task. On these evaluations, the tested Luxical model illustrates favorable compute/quality trade-offs for large-scale text organization, matching the quality of neural baselines. Luxical is available as open-source software at https://github.com/datologyai/luxical.

Identifiability of latent-variable and structural-equation models: from linear to nonlinear

An old problem in multivariate statistics is that linear Gaussian models are often unidentifiable, i.e. some parameters cannot be uniquely estimated. In factor analysis, an orthogonal rotation of the factors is unidentifiable, while in linear regression, the direction of effect cannot be identified. For such linear models, non-Gaussianity of the (latent) variables has been shown to provide identifiability. In the case of factor analysis, this leads to independent component analysis, while in the case of the direction of effect, non-Gaussian versions of structural equation modelling solve the problem. More recently, we have shown how even general nonparametric nonlinear versions of such models can be estimated. Non-Gaussianity is not enough in this case, but assuming we have time series, or that the distributions are suitably modulated by some observed auxiliary variables, the models are identifiable. This paper reviews the identifiability theory for the linear and nonlinear cases, considering both factor analytic models and structural equation models.

Robust contrastive learning and nonlinear ICA in the presence of outliers

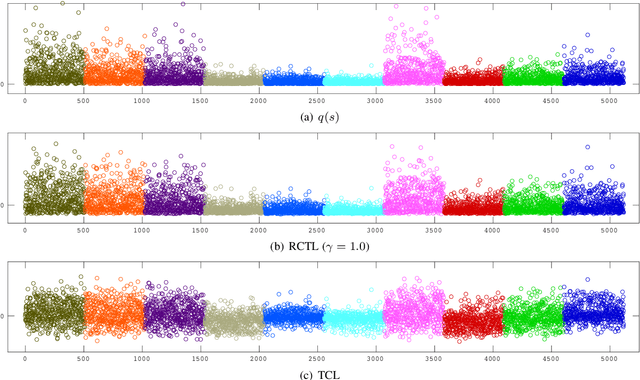
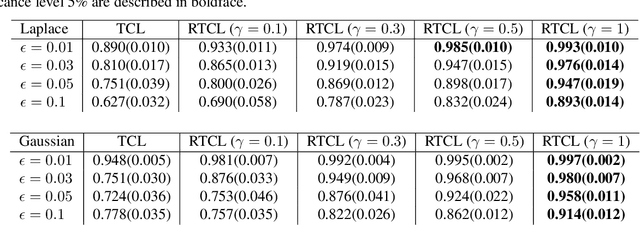
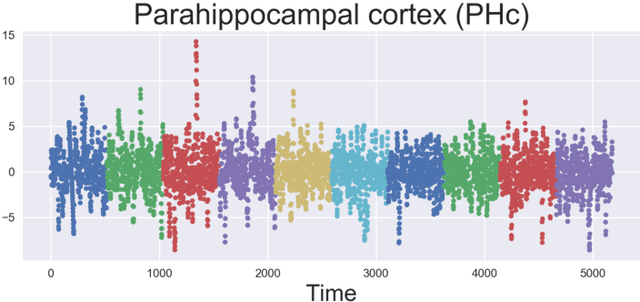
Nonlinear independent component analysis (ICA) is a general framework for unsupervised representation learning, and aimed at recovering the latent variables in data. Recent practical methods perform nonlinear ICA by solving a series of classification problems based on logistic regression. However, it is well-known that logistic regression is vulnerable to outliers, and thus the performance can be strongly weakened by outliers. In this paper, we first theoretically analyze nonlinear ICA models in the presence of outliers. Our analysis implies that estimation in nonlinear ICA can be seriously hampered when outliers exist on the tails of the (noncontaminated) target density, which happens in a typical case of contamination by outliers. We develop two robust nonlinear ICA methods based on the {\gamma}-divergence, which is a robust alternative to the KL-divergence in logistic regression. The proposed methods are shown to have desired robustness properties in the context of nonlinear ICA. We also experimentally demonstrate that the proposed methods are very robust and outperform existing methods in the presence of outliers. Finally, the proposed method is applied to ICA-based causal discovery and shown to find a plausible causal relationship on fMRI data.