DatBench: Discriminative, Faithful, and Efficient VLM Evaluations

Empirical evaluation serves as the primary compass guiding research progress in foundation models. Despite a large body of work focused on training frontier vision-language models (VLMs), approaches to their evaluation remain nascent. To guide their maturation, we propose three desiderata that evaluations should satisfy: (1) faithfulness to the modality and application, (2) discriminability between models of varying quality, and (3) efficiency in compute. Through this lens, we identify critical failure modes that violate faithfulness and discriminability, misrepresenting model capabilities: (i) multiple-choice formats reward guessing, poorly reflect downstream use cases, and saturate early as models improve; (ii) blindly solvable questions, which can be answered without images, constitute up to 70% of some evaluations; and (iii) mislabeled or ambiguous samples compromise up to 42% of examples in certain datasets. Regarding efficiency, the computational burden of evaluating frontier models has become prohibitive: by some accounts, nearly 20% of development compute is devoted to evaluation alone. Rather than discarding existing benchmarks, we curate them via transformation and filtering to maximize fidelity and discriminability. We find that converting multiple-choice questions to generative tasks reveals sharp capability drops of up to 35%. In addition, filtering blindly solvable and mislabeled samples improves discriminative power while simultaneously reducing computational cost. We release DatBench-Full, a cleaned evaluation suite of 33 datasets spanning nine VLM capabilities, and DatBench, a discriminative subset that achieves 13x average speedup (up to 50x) while closely matching the discriminative power of the original datasets. Our work outlines a path toward evaluation practices that are both rigorous and sustainable as VLMs continue to scale.

Luxical: High-Speed Lexical-Dense Text Embeddings

Frontier language model quality increasingly hinges on our ability to organize web-scale text corpora for training. Today's dominant tools trade off speed and flexibility: lexical classifiers (e.g., FastText) are fast but limited to producing classification output scores, while the vector-valued outputs of transformer text embedding models flexibly support numerous workflows (e.g., clustering, classification, and retrieval) but are computationally expensive to produce. We introduce Luxical, a library for high-speed "lexical-dense" text embeddings that aims to recover the best properties of both approaches for web-scale text organization. Luxical combines sparse TF--IDF features, a small ReLU network, and a knowledge distillation training regimen to approximate large transformer embedding models at a fraction of their operational cost. In this technical report, we describe the Luxical architecture and training objective and evaluate a concrete Luxical model in two disparate applications: a targeted webcrawl document retrieval test and an end-to-end language model data curation task grounded in text classification. In these tasks we demonstrate speedups ranging from 3x to 100x over varying-sized neural baselines, and comparable to FastText model inference during the data curation task. On these evaluations, the tested Luxical model illustrates favorable compute/quality trade-offs for large-scale text organization, matching the quality of neural baselines. Luxical is available as open-source software at https://github.com/datologyai/luxical.

Heterogeneous Graphlets

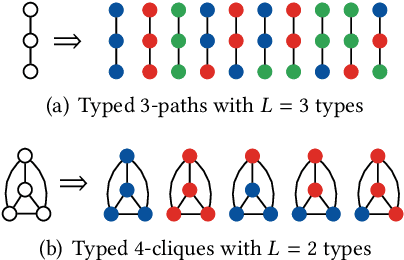
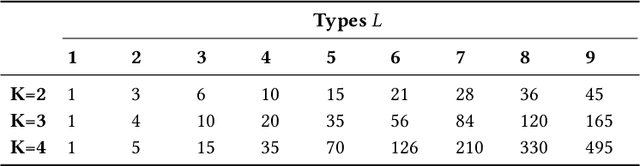
In this paper, we introduce a generalization of graphlets to heterogeneous networks called typed graphlets. Informally, typed graphlets are small typed induced subgraphs. Typed graphlets generalize graphlets to rich heterogeneous networks as they explicitly capture the higher-order typed connectivity patterns in such networks. To address this problem, we describe a general framework for counting the occurrences of such typed graphlets. The proposed algorithms leverage a number of combinatorial relationships for different typed graphlets. For each edge, we count a few typed graphlets, and with these counts along with the combinatorial relationships, we obtain the exact counts of the other typed graphlets in o(1) constant time. Notably, the worst-case time complexity of the proposed approach matches the time complexity of the best known untyped algorithm. In addition, the approach lends itself to an efficient lock-free and asynchronous parallel implementation. While there are no existing methods for typed graphlets, there has been some work that focused on computing a different and much simpler notion called colored graphlet. The experiments confirm that our proposed approach is orders of magnitude faster and more space-efficient than methods for computing the simpler notion of colored graphlet. Unlike these methods that take hours on small networks, the proposed approach takes only seconds on large networks with millions of edges. Notably, since typed graphlet is more general than colored graphlet (and untyped graphlets), the counts of various typed graphlets can be combined to obtain the counts of the much simpler notion of colored graphlets. The proposed methods give rise to new opportunities and applications for typed graphlets.

Heterogeneous Network Motifs

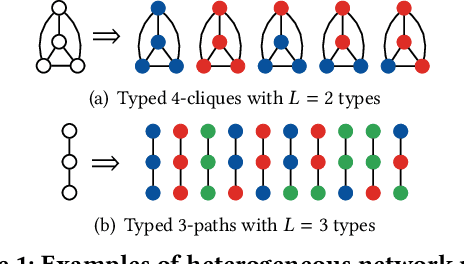
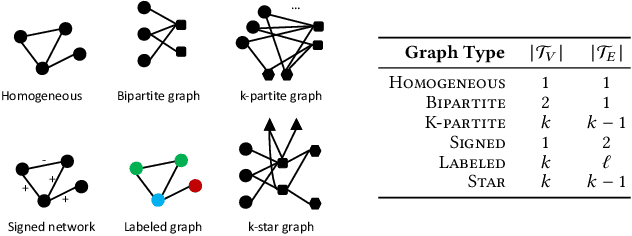
Many real-world applications give rise to large heterogeneous networks where nodes and edges can be of any arbitrary type (e.g., user, web page, location). Special cases of such heterogeneous graphs include homogeneous graphs, bipartite, k-partite, signed, labeled graphs, among many others. In this work, we generalize the notion of network motifs to heterogeneous networks. In particular, small induced typed subgraphs called typed graphlets (heterogeneous network motifs) are introduced and shown to be the fundamental building blocks of complex heterogeneous networks. Typed graphlets are a powerful generalization of the notion of graphlet (network motif) to heterogeneous networks as they capture both the induced subgraph of interest and the types associated with the nodes in the induced subgraph. To address this problem, we propose a fast, parallel, and space-efficient framework for counting typed graphlets in large networks. We discover the existence of non-trivial combinatorial relationships between lower-order ($k-1$)-node typed graphlets and leverage them for deriving many of the $k$-node typed graphlets in $o(1)$ constant time. Thus, we avoid explicit enumeration of those typed graphlets. Notably, the time complexity matches the best untyped graphlet counting algorithm. The experiments demonstrate the effectiveness of the proposed framework in terms of runtime, space-efficiency, parallel speedup, and scalability as it is able to handle large-scale networks.