DatBench: Discriminative, Faithful, and Efficient VLM Evaluations

Empirical evaluation serves as the primary compass guiding research progress in foundation models. Despite a large body of work focused on training frontier vision-language models (VLMs), approaches to their evaluation remain nascent. To guide their maturation, we propose three desiderata that evaluations should satisfy: (1) faithfulness to the modality and application, (2) discriminability between models of varying quality, and (3) efficiency in compute. Through this lens, we identify critical failure modes that violate faithfulness and discriminability, misrepresenting model capabilities: (i) multiple-choice formats reward guessing, poorly reflect downstream use cases, and saturate early as models improve; (ii) blindly solvable questions, which can be answered without images, constitute up to 70% of some evaluations; and (iii) mislabeled or ambiguous samples compromise up to 42% of examples in certain datasets. Regarding efficiency, the computational burden of evaluating frontier models has become prohibitive: by some accounts, nearly 20% of development compute is devoted to evaluation alone. Rather than discarding existing benchmarks, we curate them via transformation and filtering to maximize fidelity and discriminability. We find that converting multiple-choice questions to generative tasks reveals sharp capability drops of up to 35%. In addition, filtering blindly solvable and mislabeled samples improves discriminative power while simultaneously reducing computational cost. We release DatBench-Full, a cleaned evaluation suite of 33 datasets spanning nine VLM capabilities, and DatBench, a discriminative subset that achieves 13x average speedup (up to 50x) while closely matching the discriminative power of the original datasets. Our work outlines a path toward evaluation practices that are both rigorous and sustainable as VLMs continue to scale.

Luxical: High-Speed Lexical-Dense Text Embeddings

Frontier language model quality increasingly hinges on our ability to organize web-scale text corpora for training. Today's dominant tools trade off speed and flexibility: lexical classifiers (e.g., FastText) are fast but limited to producing classification output scores, while the vector-valued outputs of transformer text embedding models flexibly support numerous workflows (e.g., clustering, classification, and retrieval) but are computationally expensive to produce. We introduce Luxical, a library for high-speed "lexical-dense" text embeddings that aims to recover the best properties of both approaches for web-scale text organization. Luxical combines sparse TF--IDF features, a small ReLU network, and a knowledge distillation training regimen to approximate large transformer embedding models at a fraction of their operational cost. In this technical report, we describe the Luxical architecture and training objective and evaluate a concrete Luxical model in two disparate applications: a targeted webcrawl document retrieval test and an end-to-end language model data curation task grounded in text classification. In these tasks we demonstrate speedups ranging from 3x to 100x over varying-sized neural baselines, and comparable to FastText model inference during the data curation task. On these evaluations, the tested Luxical model illustrates favorable compute/quality trade-offs for large-scale text organization, matching the quality of neural baselines. Luxical is available as open-source software at https://github.com/datologyai/luxical.

No Spurious Local Minima in Deep Quadratic Networks

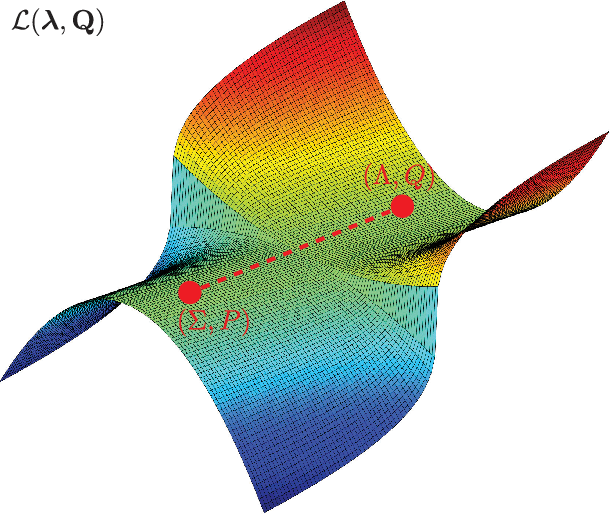
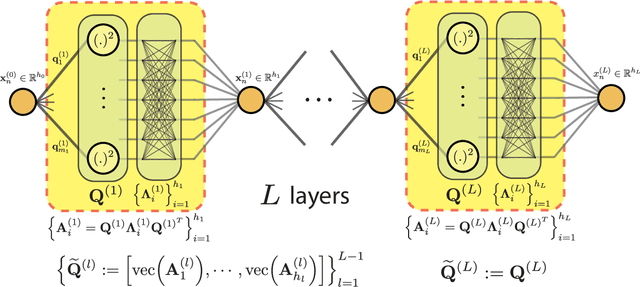
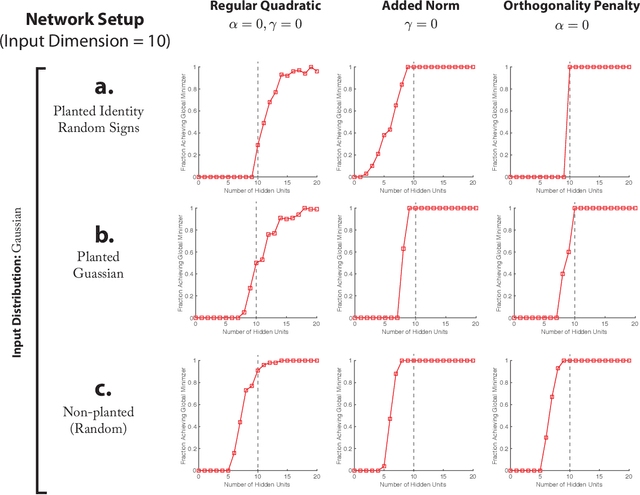
Despite their practical success, a theoretical understanding of the loss landscape of neural networks has proven challenging due to the high-dimensional, non-convex, and highly nonlinear structure of such models. In this paper, we characterize the training landscape of the quadratic loss landscape for neural networks with quadratic activation functions. We prove existence of spurious local minima and saddle points which can be escaped easily with probability one when the number of neurons is greater than or equal to the input dimension and the norm of the training samples is used as a regressor. We prove that deep overparameterized neural networks with quadratic activations benefit from similar nice landscape properties. Our theoretical results are independent of data distribution and fill the existing gap in theory for two-layer quadratic neural networks. Finally, we empirically demonstrate convergence to a global minimum for these problems.