Identifiable Multi-View Causal Discovery Without Non-Gaussianity

We propose a novel approach to linear causal discovery in the framework of multi-view Structural Equation Models (SEM). Our proposed model relaxes the well-known assumption of non-Gaussian disturbances by alternatively assuming diversity of variances over views, making it more broadly applicable. We prove the identifiability of all the parameters of the model without any further assumptions on the structure of the SEM other than it being acyclic. We further propose an estimation algorithm based on recent advances in multi-view Independent Component Analysis (ICA). The proposed methodology is validated through simulations and application on real neuroimaging data, where it enables the estimation of causal graphs between brain regions.

Density Ratio Estimation with Conditional Probability Paths

Density ratio estimation in high dimensions can be reframed as integrating a certain quantity, the time score, over probability paths which interpolate between the two densities. In practice, the time score has to be estimated based on samples from the two densities. However, existing methods for this problem remain computationally expensive and can yield inaccurate estimates. Inspired by recent advances in generative modeling, we introduce a novel framework for time score estimation, based on a conditioning variable. Choosing the conditioning variable judiciously enables a closed-form objective function. We demonstrate that, compared to previous approaches, our approach results in faster learning of the time score and competitive or better estimation accuracies of the density ratio on challenging tasks. Furthermore, we establish theoretical guarantees on the error of the estimated density ratio.

A noise-corrected Langevin algorithm and sampling by half-denoising

The Langevin algorithm is a classic method for sampling from a given pdf in a real space. In its basic version, it only requires knowledge of the gradient of the log-density, also called the score function. However, in deep learning, it is often easier to learn the so-called "noisy score function", i.e. the gradient of the log-density of noisy data, more precisely when Gaussian noise is added to the data. Such an estimate is biased and complicates the use of the Langevin method. Here, we propose a noise-corrected version of the Langevin algorithm, where the bias due to noisy data is removed, at least regarding first-order terms. Unlike diffusion models, our algorithm needs to know the noisy score function for one single noise level only. We further propose a simple special case which has an interesting intuitive interpretation of iteratively adding noise the data and then attempting to remove half of that noise.

Identifiable Feature Learning for Spatial Data with Nonlinear ICA

Recently, nonlinear ICA has surfaced as a popular alternative to the many heuristic models used in deep representation learning and disentanglement. An advantage of nonlinear ICA is that a sophisticated identifiability theory has been developed; in particular, it has been proven that the original components can be recovered under sufficiently strong latent dependencies. Despite this general theory, practical nonlinear ICA algorithms have so far been mainly limited to data with one-dimensional latent dependencies, especially time-series data. In this paper, we introduce a new nonlinear ICA framework that employs $t$-process (TP) latent components which apply naturally to data with higher-dimensional dependency structures, such as spatial and spatio-temporal data. In particular, we develop a new learning and inference algorithm that extends variational inference methods to handle the combination of a deep neural network mixing function with the TP prior, and employs the method of inducing points for computational efficacy. On the theoretical side, we show that such TP independent components are identifiable under very general conditions. Further, Gaussian Process (GP) nonlinear ICA is established as a limit of the TP Nonlinear ICA model, and we prove that the identifiability of the latent components at this GP limit is more restricted. Namely, those components are identifiable if and only if they have distinctly different covariance kernels. Our algorithm and identifiability theorems are explored on simulated spatial data and real world spatio-temporal data.

Causal Representation Learning Made Identifiable by Grouping of Observational Variables

A topic of great current interest is Causal Representation Learning (CRL), whose goal is to learn a causal model for hidden features in a data-driven manner. Unfortunately, CRL is severely ill-posed since it is a combination of the two notoriously ill-posed problems of representation learning and causal discovery. Yet, finding practical identifiability conditions that guarantee a unique solution is crucial for its practical applicability. Most approaches so far have been based on assumptions on the latent causal mechanisms, such as temporal causality, or existence of supervision or interventions; these can be too restrictive in actual applications. Here, we show identifiability based on novel, weak constraints, which requires no temporal structure, intervention, nor weak supervision. The approach is based assuming the observational mixing exhibits a suitable grouping of the observational variables. We also propose a novel self-supervised estimation framework consistent with the model, prove its statistical consistency, and experimentally show its superior CRL performances compared to the state-of-the-art baselines. We further demonstrate its robustness against latent confounders and causal cycles.

Identifiability of latent-variable and structural-equation models: from linear to nonlinear

An old problem in multivariate statistics is that linear Gaussian models are often unidentifiable, i.e. some parameters cannot be uniquely estimated. In factor analysis, an orthogonal rotation of the factors is unidentifiable, while in linear regression, the direction of effect cannot be identified. For such linear models, non-Gaussianity of the (latent) variables has been shown to provide identifiability. In the case of factor analysis, this leads to independent component analysis, while in the case of the direction of effect, non-Gaussian versions of structural equation modelling solve the problem. More recently, we have shown how even general nonparametric nonlinear versions of such models can be estimated. Non-Gaussianity is not enough in this case, but assuming we have time series, or that the distributions are suitably modulated by some observed auxiliary variables, the models are identifiable. This paper reviews the identifiability theory for the linear and nonlinear cases, considering both factor analytic models and structural equation models.

Painful intelligence: What AI can tell us about human suffering

This book uses the modern theory of artificial intelligence (AI) to understand human suffering or mental pain. Both humans and sophisticated AI agents process information about the world in order to achieve goals and obtain rewards, which is why AI can be used as a model of the human brain and mind. This book intends to make the theory accessible to a relatively general audience, requiring only some relevant scientific background. The book starts with the assumption that suffering is mainly caused by frustration. Frustration means the failure of an agent (whether AI or human) to achieve a goal or a reward it wanted or expected. Frustration is inevitable because of the overwhelming complexity of the world, limited computational resources, and scarcity of good data. In particular, such limitations imply that an agent acting in the real world must cope with uncontrollability, unpredictability, and uncertainty, which all lead to frustration. Fundamental in such modelling is the idea of learning, or adaptation to the environment. While AI uses machine learning, humans and animals adapt by a combination of evolutionary mechanisms and ordinary learning. Even frustration is fundamentally an error signal that the system uses for learning. This book explores various aspects and limitations of learning algorithms and their implications regarding suffering. At the end of the book, the computational theory is used to derive various interventions or training methods that will reduce suffering in humans. The amount of frustration is expressed by a simple equation which indicates how it can be reduced. The ensuing interventions are very similar to those proposed by Buddhist and Stoic philosophy, and include mindfulness meditation. Therefore, this book can be interpreted as an exposition of a computational theory justifying why such philosophies and meditation reduce human suffering.

Binary Independent Component Analysis via Non-stationarity

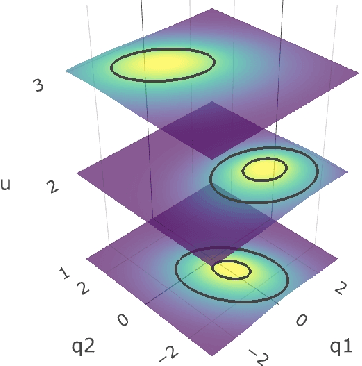
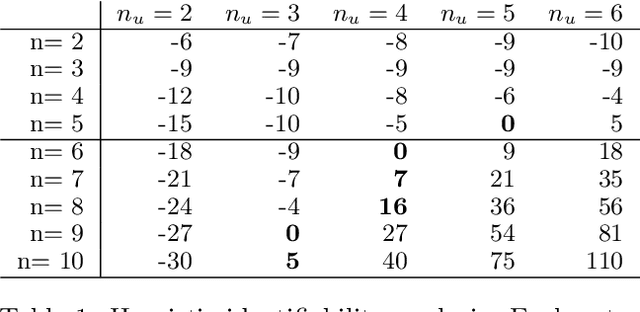
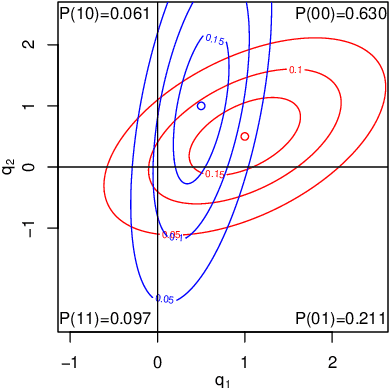
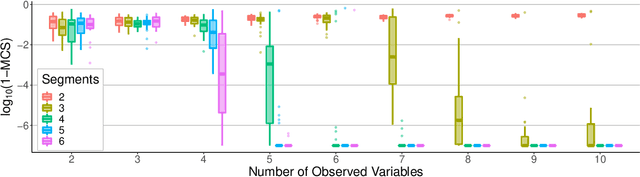
We consider independent component analysis of binary data. While fundamental in practice, this case has been much less developed than ICA for continuous data. We start by assuming a linear mixing model in a continuous-valued latent space, followed by a binary observation model. Importantly, we assume that the sources are non-stationary; this is necessary since any non-Gaussianity would essentially be destroyed by the binarization. Interestingly, the model allows for closed-form likelihood by employing the cumulative distribution function of the multivariate Gaussian distribution. In stark contrast to the continuous-valued case, we prove non-identifiability of the model with few observed variables; our empirical results imply identifiability when the number of observed variables is higher. We present a practical method for binary ICA that uses only pairwise marginals, which are faster to compute than the full multivariate likelihood.

Shared Independent Component Analysis for Multi-Subject Neuroimaging

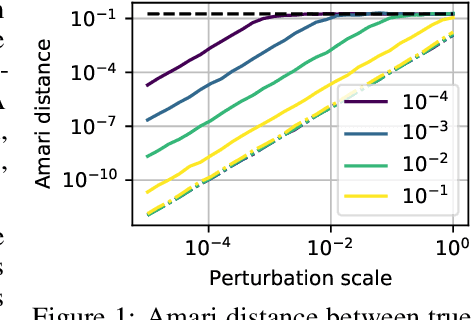
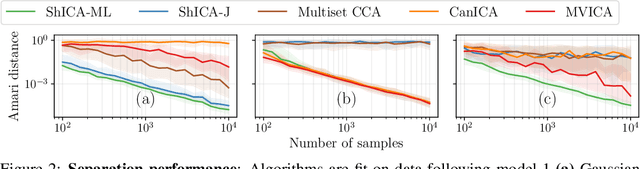
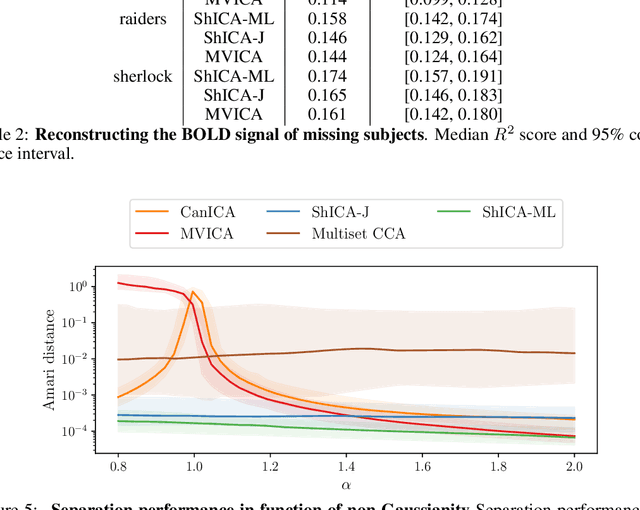
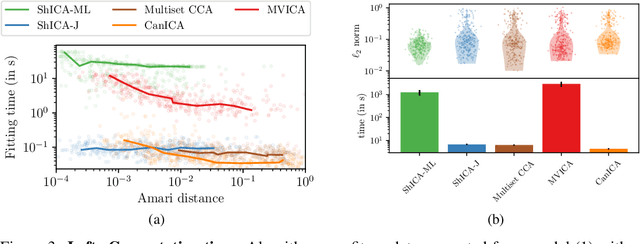
We consider shared response modeling, a multi-view learning problem where one wants to identify common components from multiple datasets or views. We introduce Shared Independent Component Analysis (ShICA) that models each view as a linear transform of shared independent components contaminated by additive Gaussian noise. We show that this model is identifiable if the components are either non-Gaussian or have enough diversity in noise variances. We then show that in some cases multi-set canonical correlation analysis can recover the correct unmixing matrices, but that even a small amount of sampling noise makes Multiset CCA fail. To solve this problem, we propose to use joint diagonalization after Multiset CCA, leading to a new approach called ShICA-J. We show via simulations that ShICA-J leads to improved results while being very fast to fit. While ShICA-J is based on second-order statistics, we further propose to leverage non-Gaussianity of the components using a maximum-likelihood method, ShICA-ML, that is both more accurate and more costly. Further, ShICA comes with a principled method for shared components estimation. Finally, we provide empirical evidence on fMRI and MEG datasets that ShICA yields more accurate estimation of the components than alternatives.

Adaptive Multi-View ICA: Estimation of noise levels for optimal inference

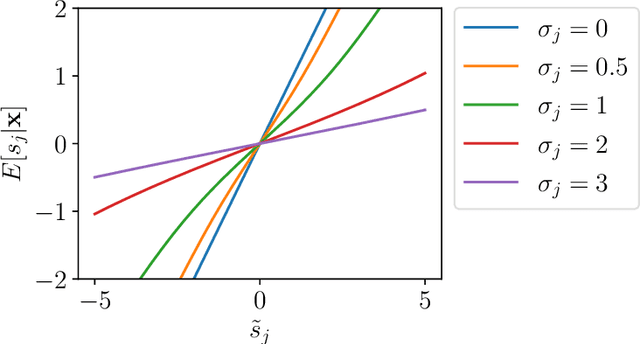
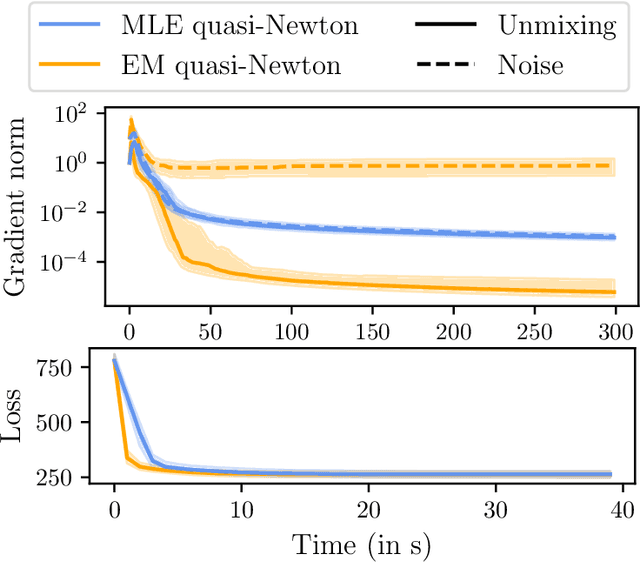
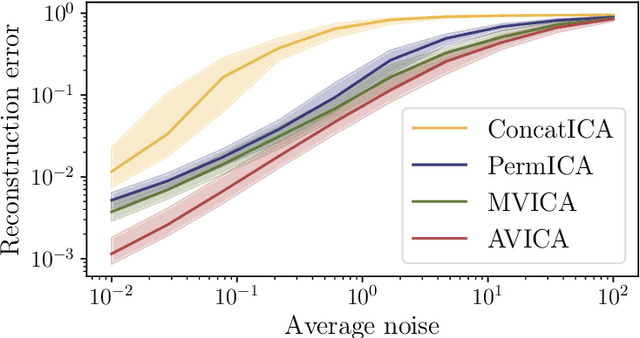
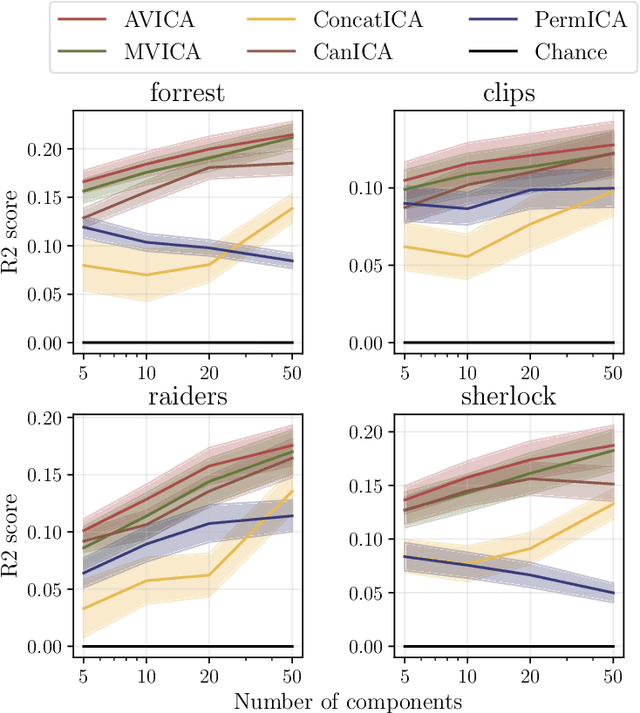
We consider a multi-view learning problem known as group independent component analysis (group ICA), where the goal is to recover shared independent sources from many views. The statistical modeling of this problem requires to take noise into account. When the model includes additive noise on the observations, the likelihood is intractable. By contrast, we propose Adaptive multiView ICA (AVICA), a noisy ICA model where each view is a linear mixture of shared independent sources with additive noise on the sources. In this setting, the likelihood has a tractable expression, which enables either direct optimization of the log-likelihood using a quasi-Newton method, or generalized EM. Importantly, we consider that the noise levels are also parameters that are learned from the data. This enables sources estimation with a closed-form Minimum Mean Squared Error (MMSE) estimator which weights each view according to its relative noise level. On synthetic data, AVICA yields better sources estimates than other group ICA methods thanks to its explicit MMSE estimator. On real magnetoencephalograpy (MEG) data, we provide evidence that the decomposition is less sensitive to sampling noise and that the noise variance estimates are biologically plausible. Lastly, on functional magnetic resonance imaging (fMRI) data, AVICA exhibits best performance in transferring information across views.