Batched Neural Bandits

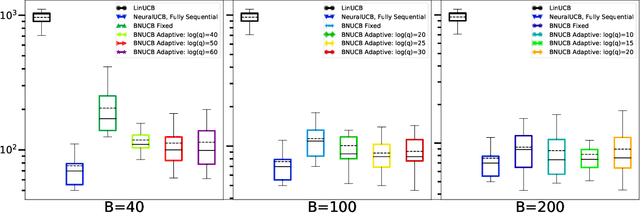
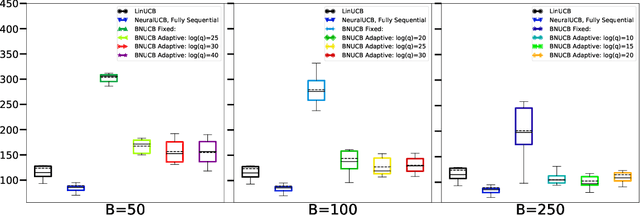
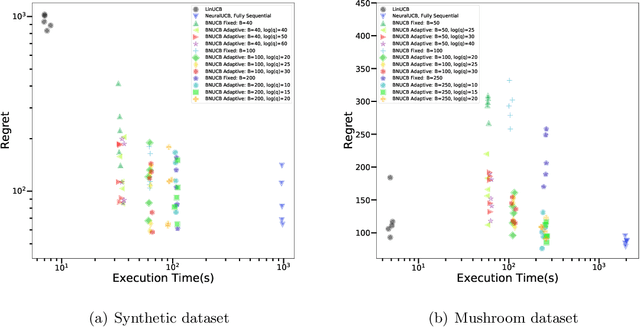
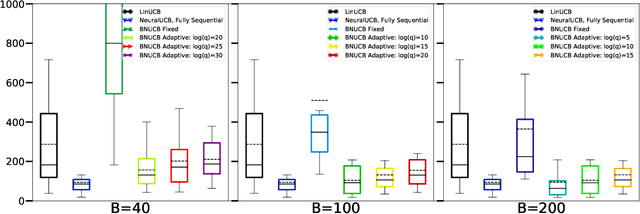
In many sequential decision-making problems, the individuals are split into several batches and the decision-maker is only allowed to change her policy at the end of batches. These batch problems have a large number of applications, ranging from clinical trials to crowdsourcing. Motivated by this, we study the stochastic contextual bandit problem for general reward distributions under the batched setting. We propose the BatchNeuralUCB algorithm which combines neural networks with optimism to address the exploration-exploitation tradeoff while keeping the total number of batches limited. We study BatchNeuralUCB under both fixed and adaptive batch size settings and prove that it achieves the same regret as the fully sequential version while reducing the number of policy updates considerably. We confirm our theoretical results via simulations on both synthetic and real-world datasets.

Nearly Optimal Regret for Learning Adversarial MDPs with Linear Function Approximation

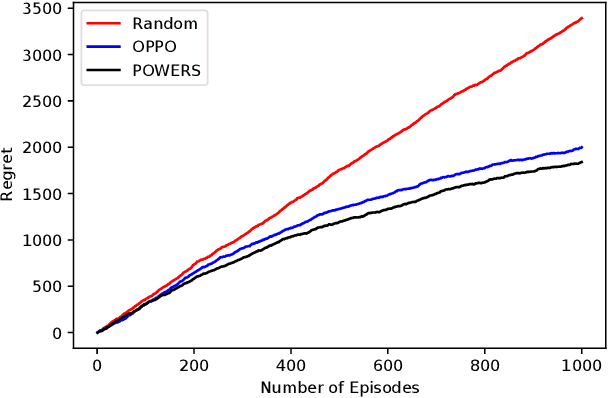
We study the reinforcement learning for finite-horizon episodic Markov decision processes with adversarial reward and full information feedback, where the unknown transition probability function is a linear function of a given feature mapping. We propose an optimistic policy optimization algorithm with Bernstein bonus and show that it can achieve $\tilde{O}(dH\sqrt{T})$ regret, where $H$ is the length of the episode, $T$ is the number of interaction with the MDP and $d$ is the dimension of the feature mapping. Furthermore, we also prove a matching lower bound of $\tilde{\Omega}(dH\sqrt{T})$ up to logarithmic factors. To the best of our knowledge, this is the first computationally efficient, nearly minimax optimal algorithm for adversarial Markov decision processes with linear function approximation.

Almost Optimal Algorithms for Two-player Markov Games with Linear Function Approximation

We study reinforcement learning for two-player zero-sum Markov games with simultaneous moves in the finite-horizon setting, where the transition kernel of the underlying Markov games can be parameterized by a linear function over the current state, both players' actions and the next state. In particular, we assume that we can control both players and aim to find the Nash Equilibrium by minimizing the duality gap. We propose an algorithm Nash-UCRL-VTR based on the principle "Optimism-in-Face-of-Uncertainty". Our algorithm only needs to find a Coarse Correlated Equilibrium (CCE), which is computationally very efficient. Specifically, we show that Nash-UCRL-VTR can provably achieve an $\tilde{O}(dH\sqrt{T})$ regret, where $d$ is the linear function dimension, $H$ is the length of the game and $T$ is the total number of steps in the game. To access the optimality of our algorithm, we also prove an $\tilde{\Omega}( dH\sqrt{T})$ lower bound on the regret. Our upper bound matches the lower bound up to logarithmic factors, which suggests the optimality of our algorithm.

Nearly Minimax Optimal Regret for Learning Infinite-horizon Average-reward MDPs with Linear Function Approximation

We study reinforcement learning in an infinite-horizon average-reward setting with linear function approximation, where the transition probability function of the underlying Markov Decision Process (MDP) admits a linear form over a feature mapping of the current state, action, and next state. We propose a new algorithm UCRL2-VTR, which can be seen as an extension of the UCRL2 algorithm with linear function approximation. We show that UCRL2-VTR with Bernstein-type bonus can achieve a regret of $\tilde{O}(d\sqrt{DT})$, where $d$ is the dimension of the feature mapping, $T$ is the horizon, and $\sqrt{D}$ is the diameter of the MDP. We also prove a matching lower bound $\tilde{\Omega}(d\sqrt{DT})$, which suggests that the proposed UCRL2-VTR is minimax optimal up to logarithmic factors. To the best of our knowledge, our algorithm is the first nearly minimax optimal RL algorithm with function approximation in the infinite-horizon average-reward setting.

Provable Generalization of SGD-trained Neural Networks of Any Width in the Presence of Adversarial Label Noise

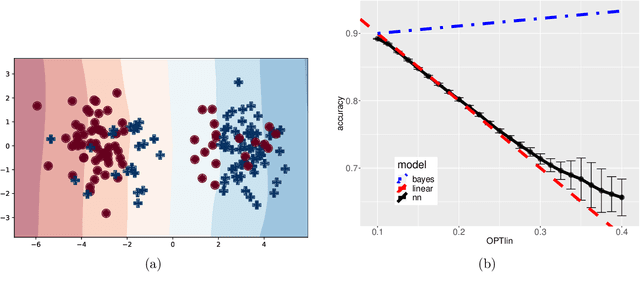
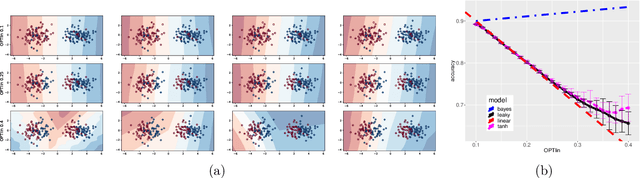
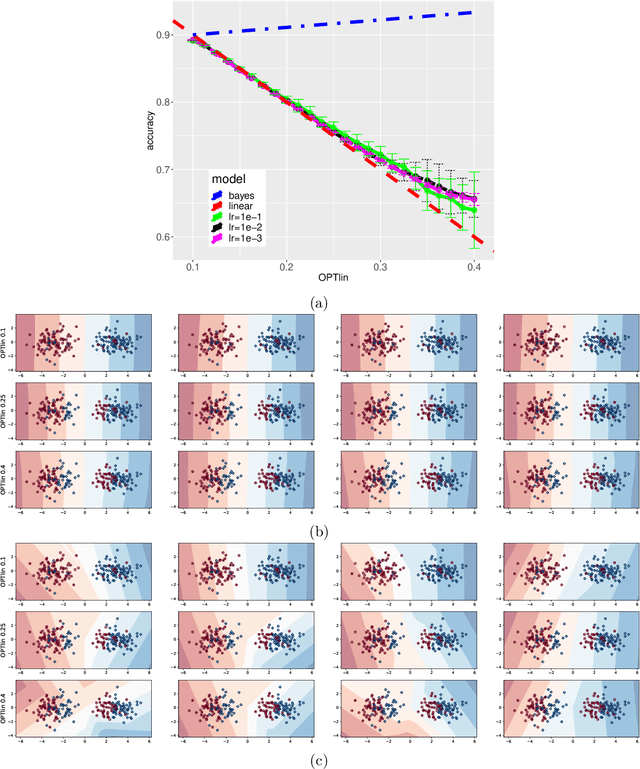
We consider a one-hidden-layer leaky ReLU network of arbitrary width trained by stochastic gradient descent following an arbitrary initialization. We prove that stochastic gradient descent (SGD) produces neural networks that have classification accuracy competitive with that of the best halfspace over the distribution for a broad class of distributions that includes log-concave isotropic and hard margin distributions. Equivalently, such networks can generalize when the data distribution is linearly separable but corrupted with adversarial label noise, despite the capacity to overfit. We conduct experiments which suggest that for some distributions our generalization bounds are nearly tight. This is the first result that shows that overparameterized neural networks trained by SGD can generalize when the data is corrupted with adversarial label noise.

Nearly Minimax Optimal Reinforcement Learning for Linear Mixture Markov Decision Processes

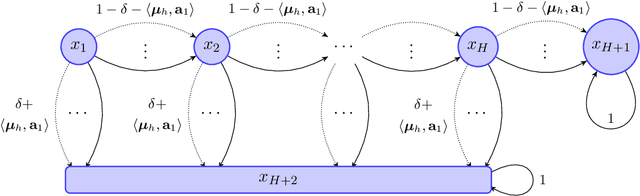
We study reinforcement learning (RL) with linear function approximation where the underlying transition probability kernel of the Markov decision process (MDP) is a linear mixture model (Jia et al., 2020; Ayoub et al., 2020; Zhou et al., 2020) and the learning agent has access to either an integration or a sampling oracle of the individual basis kernels. We propose a new Bernstein-type concentration inequality for self-normalized martingales for linear bandit problems with bounded noise. Based on the new inequality, we propose a new, computationally efficient algorithm with linear function approximation named $\text{UCRL-VTR}^{+}$ for the aforementioned linear mixture MDPs in the episodic undiscounted setting. We show that $\text{UCRL-VTR}^{+}$ attains an $\tilde O(dH\sqrt{T})$ regret where $d$ is the dimension of feature mapping, $H$ is the length of the episode and $T$ is the number of interactions with the MDP. We also prove a matching lower bound $\Omega(dH\sqrt{T})$ for this setting, which shows that $\text{UCRL-VTR}^{+}$ is minimax optimal up to logarithmic factors. In addition, we propose the $\text{UCLK}^{+}$ algorithm for the same family of MDPs under discounting and show that it attains an $\tilde O(d\sqrt{T}/(1-\gamma)^{1.5})$ regret, where $\gamma\in [0,1)$ is the discount factor. Our upper bound matches the lower bound $\Omega(d\sqrt{T}/(1-\gamma)^{1.5})$ proved by Zhou et al. (2020) up to logarithmic factors, suggesting that $\text{UCLK}^{+}$ is nearly minimax optimal. To the best of our knowledge, these are the first computationally efficient, nearly minimax optimal algorithms for RL with linear function approximation.

Provably Efficient Reinforcement Learning with Linear Function Approximation Under Adaptivity Constraints

We study reinforcement learning (RL) with linear function approximation under the adaptivity constraint. We consider two popular limited adaptivity models: batch learning model and rare policy switch model, and propose two efficient online RL algorithms for linear Markov decision processes. In specific, for the batch learning model, our proposed LSVI-UCB-Batch algorithm achieves an $\tilde O(\sqrt{d^3H^3T} + dHT/B)$ regret, where $d$ is the dimension of the feature mapping, $H$ is the episode length, $T$ is the number of interactions and $B$ is the number of batches. Our result suggests that it suffices to use only $\sqrt{T/dH}$ batches to obtain $\tilde O(\sqrt{d^3H^3T})$ regret. For the rare policy switch model, our proposed LSVI-UCB-RareSwitch algorithm enjoys an $\tilde O(\sqrt{d^3H^3T[1+T/(dH)]^{dH/B}})$ regret, which implies that $dH\log T$ policy switches suffice to obtain the $\tilde O(\sqrt{d^3H^3T})$ regret. Our algorithms achieve the same regret as the LSVI-UCB algorithm (Jin et al., 2019), yet with a substantially smaller amount of adaptivity.

Neural Contextual Bandits with Deep Representation and Shallow Exploration

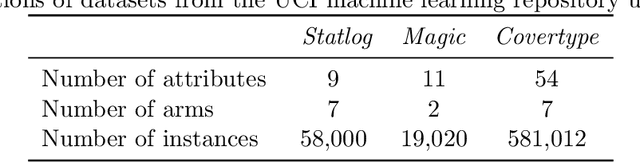
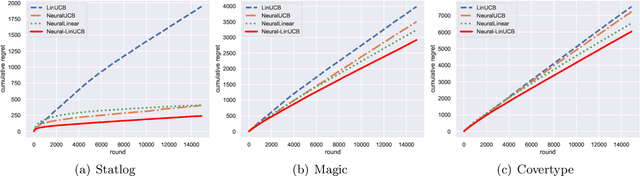
We study a general class of contextual bandits, where each context-action pair is associated with a raw feature vector, but the reward generating function is unknown. We propose a novel learning algorithm that transforms the raw feature vector using the last hidden layer of a deep ReLU neural network (deep representation learning), and uses an upper confidence bound (UCB) approach to explore in the last linear layer (shallow exploration). We prove that under standard assumptions, our proposed algorithm achieves $\tilde{O}(\sqrt{T})$ finite-time regret, where $T$ is the learning time horizon. Compared with existing neural contextual bandit algorithms, our approach is computationally much more efficient since it only needs to explore in the last layer of the deep neural network.

Logarithmic Regret for Reinforcement Learning with Linear Function Approximation

Reinforcement learning (RL) with linear function approximation has received increasing attention recently. However, existing work has focused on obtaining $\sqrt{T}$-type regret bound, where $T$ is the number of steps. In this paper, we show that logarithmic regret is attainable under two recently proposed linear MDP assumptions provided that there exists a positive sub-optimality gap for the optimal action-value function. In specific, under the linear MDP assumption (Jin et al. 2019), the LSVI-UCB algorithm can achieve $\tilde{O}(d^{3}H^5/\text{gap}_{\text{min}}\cdot \log(T))$ regret; and under the linear mixture model assumption (Ayoub et al. 2020), the UCRL-VTR algorithm can achieve $\tilde{O}(d^{2}H^5/\text{gap}_{\text{min}}\cdot \log^3(T))$ regret, where $d$ is the dimension of feature mapping, $H$ is the length of episode, and $\text{gap}_{\text{min}}$ is the minimum of sub-optimality gap. To the best of our knowledge, these are the first logarithmic regret bounds for RL with linear function approximation.

Provable Multi-Objective Reinforcement Learning with Generative Models

Multi-objective reinforcement learning (MORL) is an extension of ordinary, single-objective reinforcement learning (RL) that is applicable to many real world tasks where multiple objectives exist without known relative costs. We study the problem of single policy MORL, which learns an optimal policy given the preference of objectives. Existing methods require strong assumptions such as exact knowledge of the multi-objective Markov decision process, and are analyzed in the limit of infinite data and time. We propose a new algorithm called model-based envelop value iteration (EVI), which generalizes the enveloped multi-objective $Q$-learning algorithm in Yang, 2019. Our method can learn a near-optimal value function with polynomial sample complexity and linear convergence speed. To the best of our knowledge, this is the first finite-sample analysis of MORL algorithms.