Near-Optimal Streaming Heavy-Tailed Statistical Estimation with Clipped SGD

We consider the problem of high-dimensional heavy-tailed statistical estimation in the streaming setting, which is much harder than the traditional batch setting due to memory constraints. We cast this problem as stochastic convex optimization with heavy tailed stochastic gradients, and prove that the widely used Clipped-SGD algorithm attains near-optimal sub-Gaussian statistical rates whenever the second moment of the stochastic gradient noise is finite. More precisely, with $T$ samples, we show that Clipped-SGD, for smooth and strongly convex objectives, achieves an error of $\sqrt{\frac{\mathsf{Tr}(\Sigma)+\sqrt{\mathsf{Tr}(\Sigma)\|\Sigma\|_2}\log(\frac{\log(T)}{\delta})}{T}}$ with probability $1-\delta$, where $\Sigma$ is the covariance of the clipped gradient. Note that the fluctuations (depending on $\frac{1}{\delta}$) are of lower order than the term $\mathsf{Tr}(\Sigma)$. This improves upon the current best rate of $\sqrt{\frac{\mathsf{Tr}(\Sigma)\log(\frac{1}{\delta})}{T}}$ for Clipped-SGD, known only for smooth and strongly convex objectives. Our results also extend to smooth convex and lipschitz convex objectives. Key to our result is a novel iterative refinement strategy for martingale concentration, improving upon the PAC-Bayes approach of Catoni and Giulini.

Convex Distillation: Efficient Compression of Deep Networks via Convex Optimization

Deploying large and complex deep neural networks on resource-constrained edge devices poses significant challenges due to their computational demands and the complexities of non-convex optimization. Traditional compression methods such as distillation and pruning often retain non-convexity that complicates fine-tuning in real-time on such devices. Moreover, these methods often necessitate extensive end-to-end network fine-tuning after compression to preserve model performance, which is not only time-consuming but also requires fully annotated datasets, thus potentially negating the benefits of efficient network compression. In this paper, we introduce a novel distillation technique that efficiently compresses the model via convex optimization -- eliminating intermediate non-convex activation functions and using only intermediate activations from the original model. Our approach enables distillation in a label-free data setting and achieves performance comparable to the original model without requiring any post-compression fine-tuning. We demonstrate the effectiveness of our method for image classification models on multiple standard datasets, and further show that in the data limited regime, our method can outperform standard non-convex distillation approaches. Our method promises significant advantages for deploying high-efficiency, low-footprint models on edge devices, making it a practical choice for real-world applications. We show that convex neural networks, when provided with rich feature representations from a large pre-trained non-convex model, can achieve performance comparable to their non-convex counterparts, opening up avenues for future research at the intersection of convex optimization and deep learning.

Private and Efficient Meta-Learning with Low Rank and Sparse Decomposition

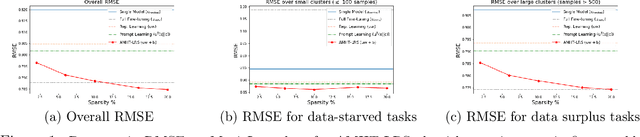
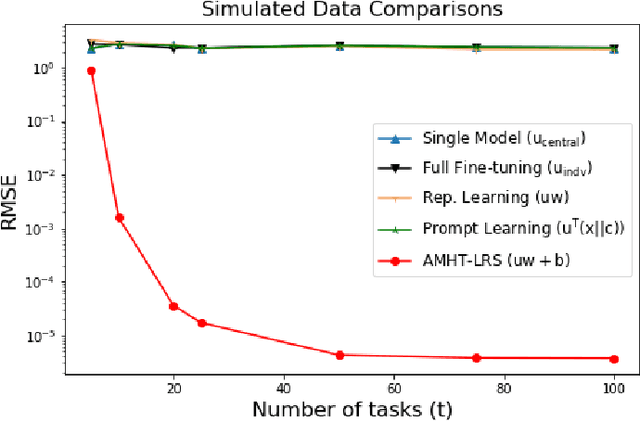
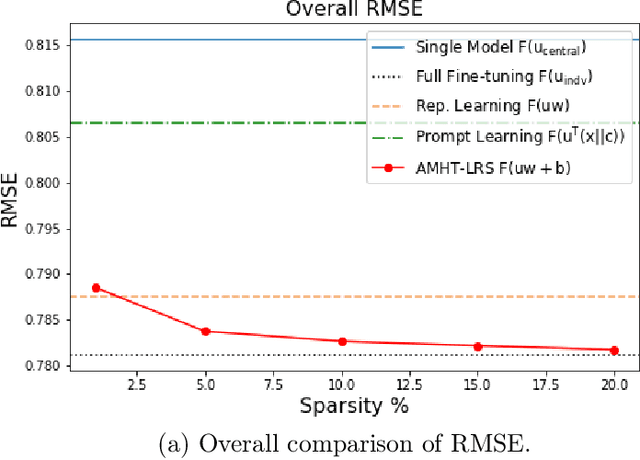
Meta-learning is critical for a variety of practical ML systems -- like personalized recommendations systems -- that are required to generalize to new tasks despite a small number of task-specific training points. Existing meta-learning techniques use two complementary approaches of either learning a low-dimensional representation of points for all tasks, or task-specific fine-tuning of a global model trained using all the tasks. In this work, we propose a novel meta-learning framework that combines both the techniques to enable handling of a large number of data-starved tasks. Our framework models network weights as a sum of low-rank and sparse matrices. This allows us to capture information from multiple domains together in the low-rank part while still allowing task specific personalization using the sparse part. We instantiate and study the framework in the linear setting, where the problem reduces to that of estimating the sum of a rank-$r$ and a $k$-column sparse matrix using a small number of linear measurements. We propose an alternating minimization method with hard thresholding -- AMHT-LRS -- to learn the low-rank and sparse part effectively and efficiently. For the realizable, Gaussian data setting, we show that AMHT-LRS indeed solves the problem efficiently with nearly optimal samples. We extend AMHT-LRS to ensure that it preserves privacy of each individual user in the dataset, while still ensuring strong generalization with nearly optimal number of samples. Finally, on multiple datasets, we demonstrate that the framework allows personalized models to obtain superior performance in the data-scarce regime.

(Nearly) Optimal Private Linear Regression via Adaptive Clipping

We study the problem of differentially private linear regression where each data point is sampled from a fixed sub-Gaussian style distribution. We propose and analyze a one-pass mini-batch stochastic gradient descent method (DP-AMBSSGD) where points in each iteration are sampled without replacement. Noise is added for DP but the noise standard deviation is estimated online. Compared to existing $(\epsilon, \delta)$-DP techniques which have sub-optimal error bounds, DP-AMBSSGD is able to provide nearly optimal error bounds in terms of key parameters like dimensionality $d$, number of points $N$, and the standard deviation $\sigma$ of the noise in observations. For example, when the $d$-dimensional covariates are sampled i.i.d. from the normal distribution, then the excess error of DP-AMBSSGD due to privacy is $\frac{\sigma^2 d}{N}(1+\frac{d}{\epsilon^2 N})$, i.e., the error is meaningful when number of samples $N= \Omega(d \log d)$ which is the standard operative regime for linear regression. In contrast, error bounds for existing efficient methods in this setting are: $\mathcal{O}\big(\frac{d^3}{\epsilon^2 N^2}\big)$, even for $\sigma=0$. That is, for constant $\epsilon$, the existing techniques require $N=\Omega(d\sqrt{d})$ to provide a non-trivial result.

CS-NET at SemEval-2020 Task 4: Siamese BERT for ComVE

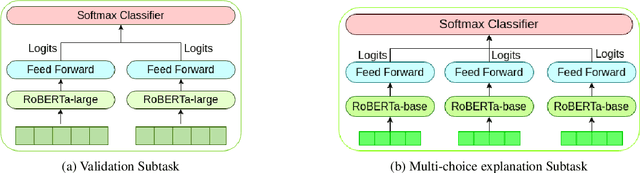
In this paper, we describe our system for Task 4 of SemEval 2020, which involves differentiating between natural language statements that confirm to common sense and those that do not. The organizers propose three subtasks - first, selecting between two sentences, the one which is against common sense. Second, identifying the most crucial reason why a statement does not make sense. Third, generating novel reasons for explaining the against common sense statement. Out of the three subtasks, this paper reports the system description of subtask A and subtask B. This paper proposes a model based on transformer neural network architecture for addressing the subtasks. The novelty in work lies in the architecture design, which handles the logical implication of contradicting statements and simultaneous information extraction from both sentences. We use a parallel instance of transformers, which is responsible for a boost in the performance. We achieved an accuracy of 94.8% in subtask A and 89% in subtask B on the test set.