Pranjal Awasthi
Measuring Model Fairness under Noisy Covariates: A Theoretical Perspective
May 20, 2021
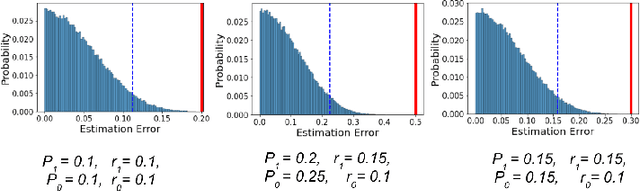
Abstract:In this work we study the problem of measuring the fairness of a machine learning model under noisy information. Focusing on group fairness metrics, we investigate the particular but common situation when the evaluation requires controlling for the confounding effect of covariate variables. In a practical setting, we might not be able to jointly observe the covariate and group information, and a standard workaround is to then use proxies for one or more of these variables. Prior works have demonstrated the challenges with using a proxy for sensitive attributes, and strong independence assumptions are needed to provide guarantees on the accuracy of the noisy estimates. In contrast, in this work we study using a proxy for the covariate variable and present a theoretical analysis that aims to characterize weaker conditions under which accurate fairness evaluation is possible. Furthermore, our theory identifies potential sources of errors and decouples them into two interpretable parts $\gamma$ and $\epsilon$. The first part $\gamma$ depends solely on the performance of the proxy such as precision and recall, whereas the second part $\epsilon$ captures correlations between all the variables of interest. We show that in many scenarios the error in the estimates is dominated by $\gamma$ via a linear dependence, whereas the dependence on the correlations $\epsilon$ only constitutes a lower order term. As a result we expand the understanding of scenarios where measuring model fairness via proxies can be an effective approach. Finally, we compare, via simulations, the theoretical upper-bounds to the distribution of simulated estimation errors and show that assuming some structure on the data, even weak, is key to significantly improve both theoretical guarantees and empirical results.
A Finer Calibration Analysis for Adversarial Robustness
May 06, 2021Abstract:We present a more general analysis of $H$-calibration for adversarially robust classification. By adopting a finer definition of calibration, we can cover settings beyond the restricted hypothesis sets studied in previous work. In particular, our results hold for most common hypothesis sets used in machine learning. We both fix some previous calibration results (Bao et al., 2020) and generalize others (Awasthi et al., 2021). Moreover, our calibration results, combined with the previous study of consistency by Awasthi et al. (2021), also lead to more general $H$-consistency results covering common hypothesis sets.
Calibration and Consistency of Adversarial Surrogate Losses
May 04, 2021

Abstract:Adversarial robustness is an increasingly critical property of classifiers in applications. The design of robust algorithms relies on surrogate losses since the optimization of the adversarial loss with most hypothesis sets is NP-hard. But which surrogate losses should be used and when do they benefit from theoretical guarantees? We present an extensive study of this question, including a detailed analysis of the H-calibration and H-consistency of adversarial surrogate losses. We show that, under some general assumptions, convex loss functions, or the supremum-based convex losses often used in applications, are not H-calibrated for important hypothesis sets such as generalized linear models or one-layer neural networks. We then give a characterization of H-calibration and prove that some surrogate losses are indeed H-calibrated for the adversarial loss, with these hypothesis sets. Next, we show that H-calibration is not sufficient to guarantee consistency and prove that, in the absence of any distributional assumption, no continuous surrogate loss is consistent in the adversarial setting. This, in particular, proves that a claim presented in a COLT 2020 publication is inaccurate. (Calibration results there are correct modulo subtle definition differences, but the consistency claim does not hold.) Next, we identify natural conditions under which some surrogate losses that we describe in detail are H-consistent for hypothesis sets such as generalized linear models and one-layer neural networks. We also report a series of empirical results with simulated data, which show that many H-calibrated surrogate losses are indeed not H-consistent, and validate our theoretical assumptions.
A Multiclass Boosting Framework for Achieving Fast and Provable Adversarial Robustness
Mar 03, 2021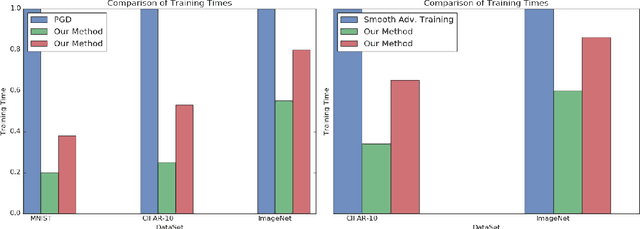
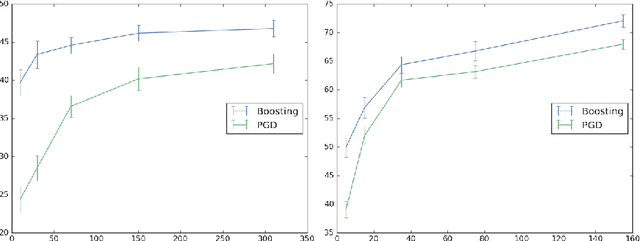

Abstract:Alongside the well-publicized accomplishments of deep neural networks there has emerged an apparent bug in their success on tasks such as object recognition: with deep models trained using vanilla methods, input images can be slightly corrupted in order to modify output predictions, even when these corruptions are practically invisible. This apparent lack of robustness has led researchers to propose methods that can help to prevent an adversary from having such capabilities. The state-of-the-art approaches have incorporated the robustness requirement into the loss function, and the training process involves taking stochastic gradient descent steps not using original inputs but on adversarially-corrupted ones. In this paper we propose a multiclass boosting framework to ensure adversarial robustness. Boosting algorithms are generally well-suited for adversarial scenarios, as they were classically designed to satisfy a minimax guarantee. We provide a theoretical foundation for this methodology and describe conditions under which robustness can be achieved given a weak training oracle. We show empirically that adversarially-robust multiclass boosting not only outperforms the state-of-the-art methods, it does so at a fraction of the training time.
Evaluating Fairness of Machine Learning Models Under Uncertain and Incomplete Information
Feb 16, 2021
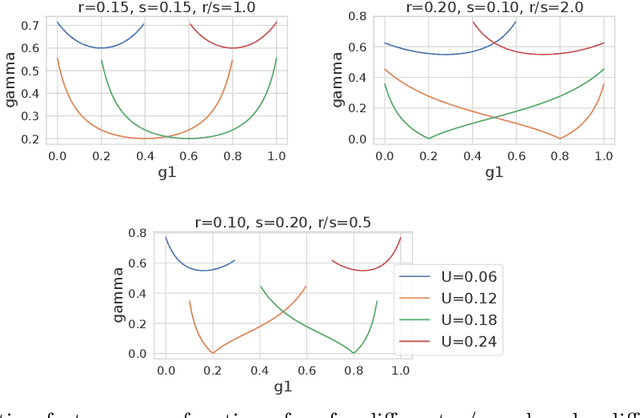


Abstract:Training and evaluation of fair classifiers is a challenging problem. This is partly due to the fact that most fairness metrics of interest depend on both the sensitive attribute information and label information of the data points. In many scenarios it is not possible to collect large datasets with such information. An alternate approach that is commonly used is to separately train an attribute classifier on data with sensitive attribute information, and then use it later in the ML pipeline to evaluate the bias of a given classifier. While such decoupling helps alleviate the problem of demographic scarcity, it raises several natural questions such as: how should the attribute classifier be trained?, and how should one use a given attribute classifier for accurate bias estimation? In this work we study this question from both theoretical and empirical perspectives. We first experimentally demonstrate that the test accuracy of the attribute classifier is not always correlated with its effectiveness in bias estimation for a downstream model. In order to further investigate this phenomenon, we analyze an idealized theoretical model and characterize the structure of the optimal classifier. Our analysis has surprising and counter-intuitive implications where in certain regimes one might want to distribute the error of the attribute classifier as unevenly as possible among the different subgroups. Based on our analysis we develop heuristics for both training and using attribute classifiers for bias estimation in the data scarce regime. We empirically demonstrate the effectiveness of our approach on real and simulated data.
Adversarial Robustness Across Representation Spaces
Dec 01, 2020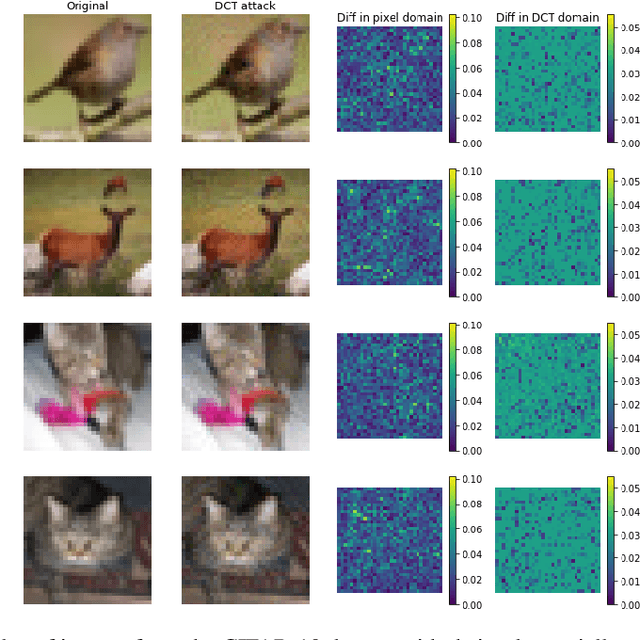
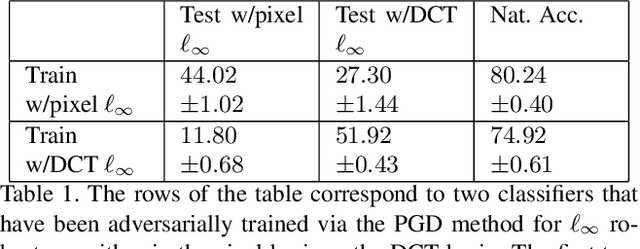

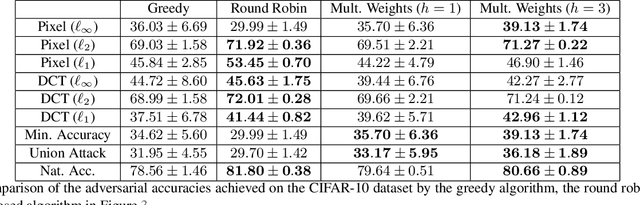
Abstract:Adversarial robustness corresponds to the susceptibility of deep neural networks to imperceptible perturbations made at test time. In the context of image tasks, many algorithms have been proposed to make neural networks robust to adversarial perturbations made to the input pixels. These perturbations are typically measured in an $\ell_p$ norm. However, robustness often holds only for the specific attack used for training. In this work we extend the above setting to consider the problem of training of deep neural networks that can be made simultaneously robust to perturbations applied in multiple natural representation spaces. For the case of image data, examples include the standard pixel representation as well as the representation in the discrete cosine transform~(DCT) basis. We design a theoretically sound algorithm with formal guarantees for the above problem. Furthermore, our guarantees also hold when the goal is to require robustness with respect to multiple $\ell_p$ norm based attacks. We then derive an efficient practical implementation and demonstrate the effectiveness of our approach on standard datasets for image classification.
Beyond Individual and Group Fairness
Aug 21, 2020



Abstract:We present a new data-driven model of fairness that, unlike existing static definitions of individual or group fairness is guided by the unfairness complaints received by the system. Our model supports multiple fairness criteria and takes into account their potential incompatibilities. We consider both a stochastic and an adversarial setting of our model. In the stochastic setting, we show that our framework can be naturally cast as a Markov Decision Process with stochastic losses, for which we give efficient vanishing regret algorithmic solutions. In the adversarial setting, we design efficient algorithms with competitive ratio guarantees. We also report the results of experiments with our algorithms and the stochastic framework on artificial datasets, to demonstrate their effectiveness empirically.
Adversarial robustness via robust low rank representations
Aug 01, 2020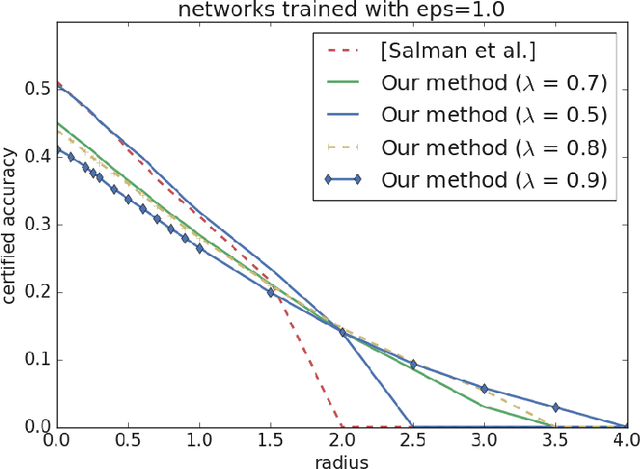

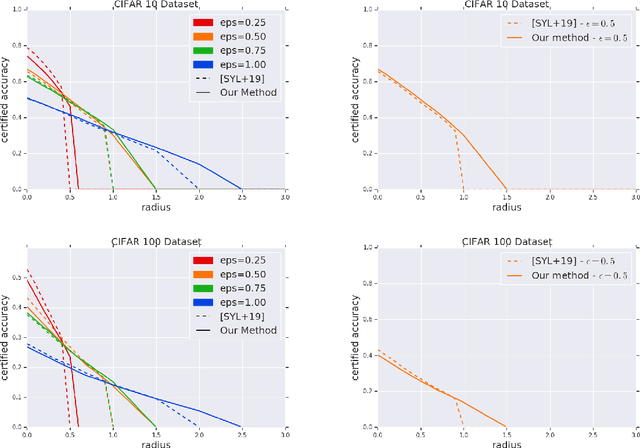
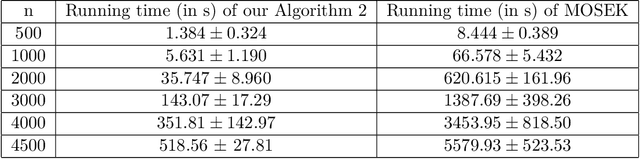
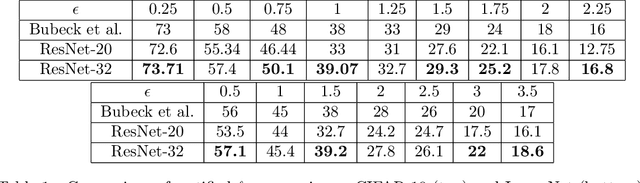
Abstract:Adversarial robustness measures the susceptibility of a classifier to imperceptible perturbations made to the inputs at test time. In this work we highlight the benefits of natural low rank representations that often exist for real data such as images, for training neural networks with certified robustness guarantees. Our first contribution is for certified robustness to perturbations measured in $\ell_2$ norm. We exploit low rank data representations to provide improved guarantees over state-of-the-art randomized smoothing-based approaches on standard benchmark datasets such as CIFAR-10 and CIFAR-100. Our second contribution is for the more challenging setting of certified robustness to perturbations measured in $\ell_\infty$ norm. We demonstrate empirically that natural low rank representations have inherent robustness properties, that can be leveraged to provide significantly better guarantees for certified robustness to $\ell_\infty$ perturbations in those representations. Our certificate of $\ell_\infty$ robustness relies on a natural quantity involving the $\infty \to 2$ matrix operator norm associated with the representation, to translate robustness guarantees from $\ell_2$ to $\ell_\infty$ perturbations. A key technical ingredient for our certification guarantees is a fast algorithm with provable guarantees based on the multiplicative weights update method to provide upper bounds on the above matrix norm. Our algorithmic guarantees improve upon the state of the art for this problem, and may be of independent interest.
On the Rademacher Complexity of Linear Hypothesis Sets
Jul 21, 2020

Abstract:Linear predictors form a rich class of hypotheses used in a variety of learning algorithms. We present a tight analysis of the empirical Rademacher complexity of the family of linear hypothesis classes with weight vectors bounded in $\ell_p$-norm for any $p \geq 1$. This provides a tight analysis of generalization using these hypothesis sets and helps derive sharp data-dependent learning guarantees. We give both upper and lower bounds on the Rademacher complexity of these families and show that our bounds improve upon or match existing bounds, which are known only for $1 \leq p \leq 2$.
Adaptive Sampling to Reduce Disparate Performance
Jun 11, 2020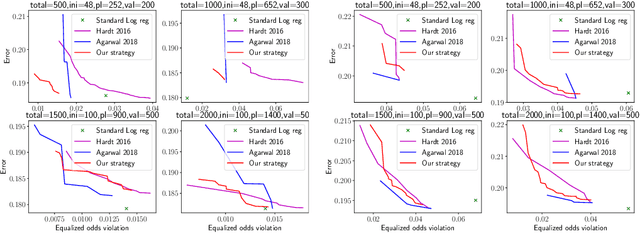
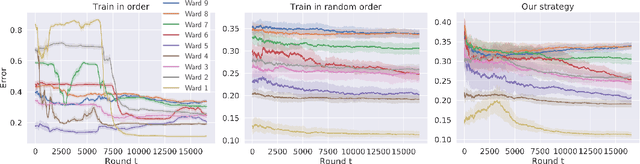
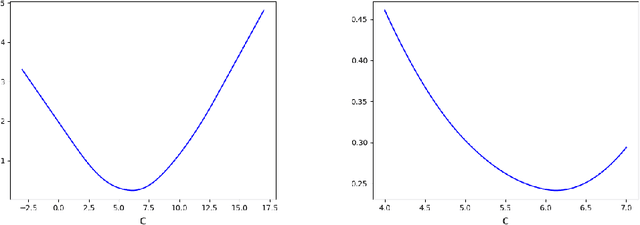
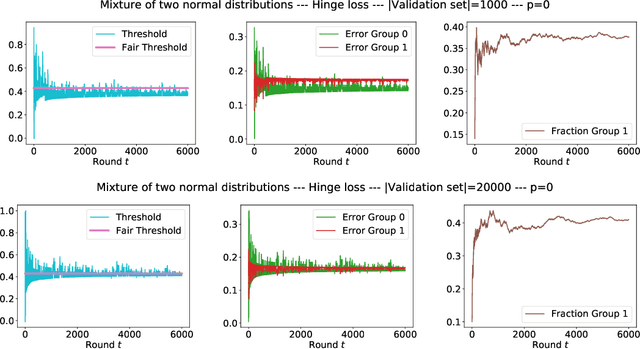
Abstract:Existing methods for reducing disparate performance of a classifier across different demographic groups assume that one has access to a large data set, thereby focusing on the algorithmic aspect of optimizing overall performance subject to additional constraints. However, poor data collection and imbalanced data sets can severely affect the quality of these methods. In this work, we consider a setting where data collection and optimization are performed simultaneously. In such a scenario, a natural strategy to mitigate the performance difference of the classifier is to provide additional training data drawn from the demographic groups that are worse off. In this paper, we propose to consistently follow this strategy throughout the whole training process and to guide the resulting classifier towards equal performance on the different groups by adaptively sampling each data point from the group that is currently disadvantaged. We provide a rigorous theoretical analysis of our approach in a simplified one-dimensional setting and an extensive experimental evaluation on numerous real-world data sets, including a case study on the data collected during the Flint water crisis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge