Ping Ma
Sufficient dimension reduction for classification using principal optimal transport direction
Oct 21, 2020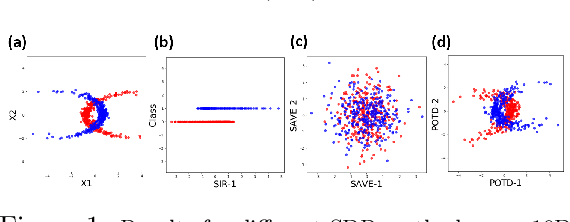
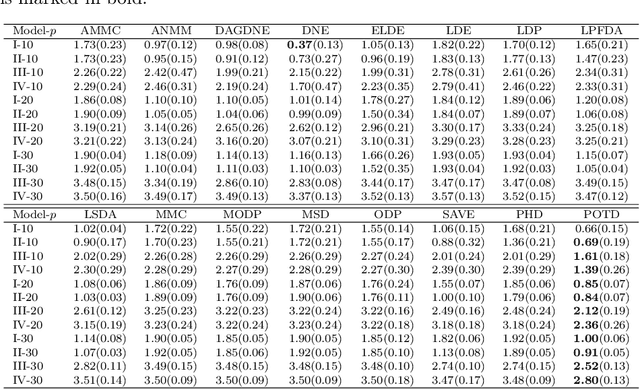
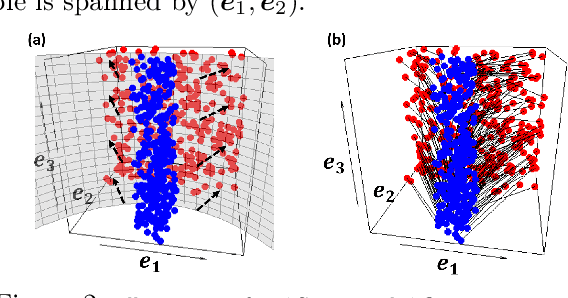
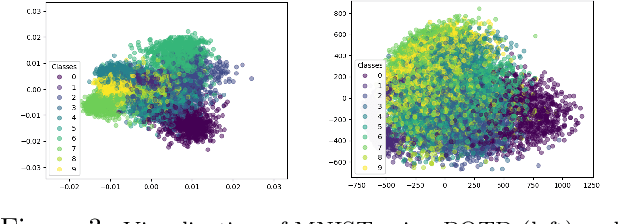
Abstract:Sufficient dimension reduction is used pervasively as a supervised dimension reduction approach. Most existing sufficient dimension reduction methods are developed for data with a continuous response and may have an unsatisfactory performance for the categorical response, especially for the binary-response. To address this issue, we propose a novel estimation method of sufficient dimension reduction subspace (SDR subspace) using optimal transport. The proposed method, named principal optimal transport direction (POTD), estimates the basis of the SDR subspace using the principal directions of the optimal transport coupling between the data respecting different response categories. The proposed method also reveals the relationship among three seemingly irrelevant topics, i.e., sufficient dimension reduction, support vector machine, and optimal transport. We study the asymptotic properties of POTD and show that in the cases when the class labels contain no error, POTD estimates the SDR subspace exclusively. Empirical studies show POTD outperforms most of the state-of-the-art linear dimension reduction methods.
A Review on Modern Computational Optimal Transport Methods with Applications in Biomedical Research
Sep 10, 2020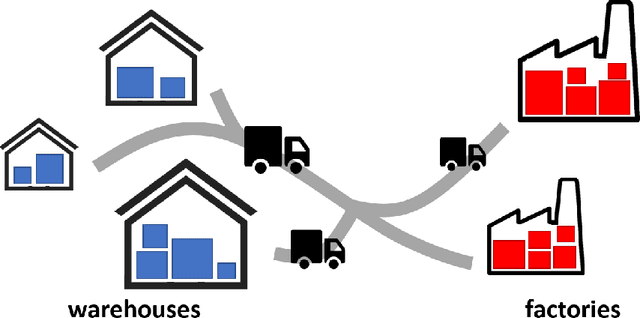
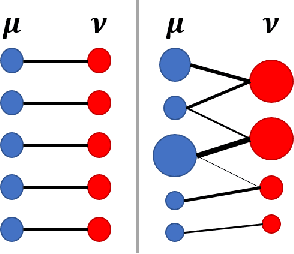
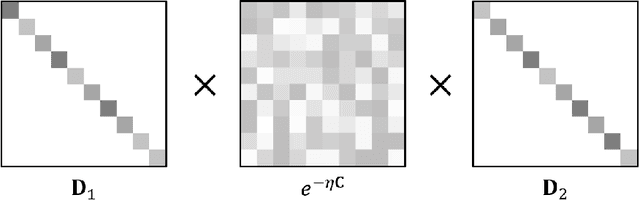
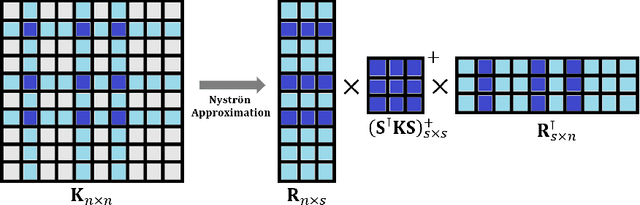
Abstract:Optimal transport has been one of the most exciting subjects in mathematics, starting from the 18th century. As a powerful tool to transport between two probability measures, optimal transport methods have been reinvigorated nowadays in a remarkable proliferation of modern data science applications. To meet the big data challenges, various computational tools have been developed in the recent decade to accelerate the computation for optimal transport methods. In this review, we present some cutting-edge computational optimal transport methods with a focus on the regularization-based methods and the projection-based methods. We discuss their real-world applications in biomedical research.
Asymptotic Analysis of Sampling Estimators for Randomized Numerical Linear Algebra Algorithms
Feb 24, 2020
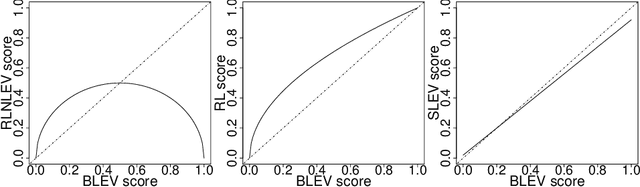
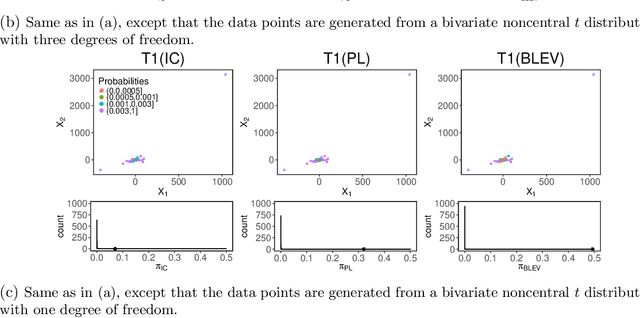
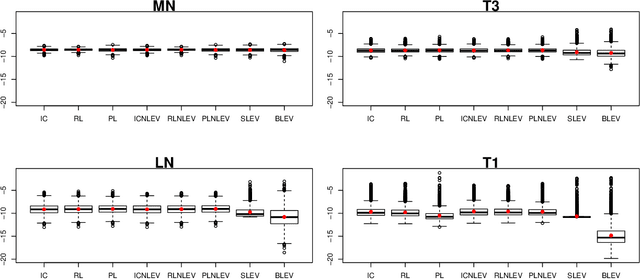
Abstract:The statistical analysis of Randomized Numerical Linear Algebra (RandNLA) algorithms within the past few years has mostly focused on their performance as point estimators. However, this is insufficient for conducting statistical inference, e.g., constructing confidence intervals and hypothesis testing, since the distribution of the estimator is lacking. In this article, we develop an asymptotic analysis to derive the distribution of RandNLA sampling estimators for the least-squares problem. In particular, we derive the asymptotic distribution of a general sampling estimator with arbitrary sampling probabilities. The analysis is conducted in two complementary settings, i.e., when the objective of interest is to approximate the full sample estimator or is to infer the underlying ground truth model parameters. For each setting, we show that the sampling estimator is asymptotically normally distributed under mild regularity conditions. Moreover, the sampling estimator is asymptotically unbiased in both settings. Based on our asymptotic analysis, we use two criteria, the Asymptotic Mean Squared Error (AMSE) and the Expected Asymptotic Mean Squared Error (EAMSE), to identify optimal sampling probabilities. Several of these optimal sampling probability distributions are new to the literature, e.g., the root leverage sampling estimator and the predictor length sampling estimator. Our theoretical results clarify the role of leverage in the sampling process, and our empirical results demonstrate improvements over existing methods.
Minimax Nonparametric Two-sample Test
Nov 08, 2019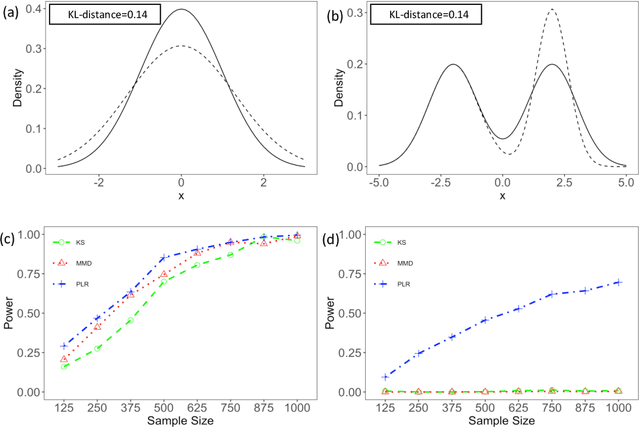
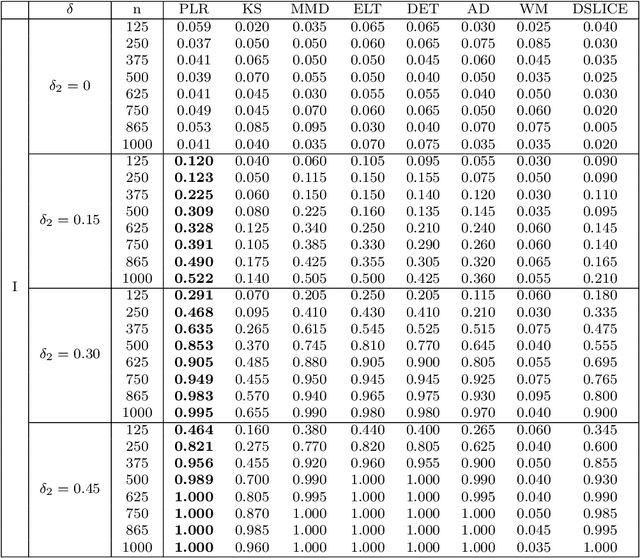
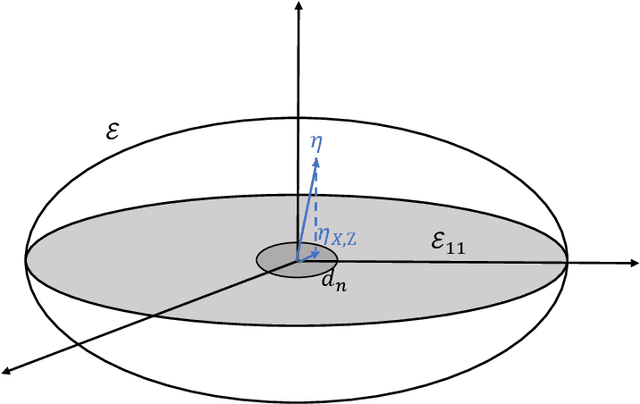
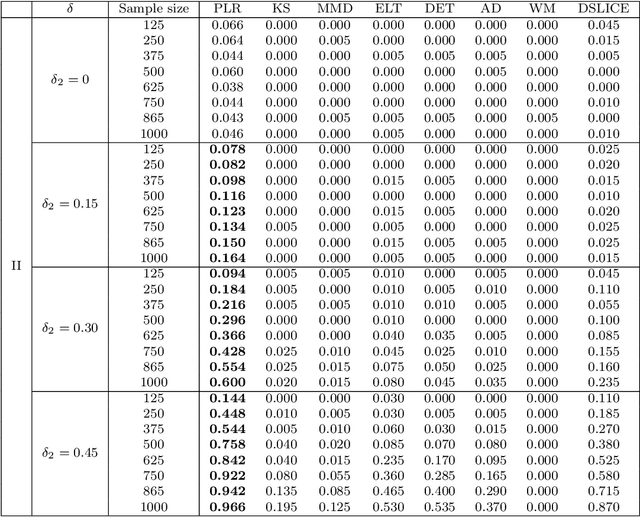
Abstract:We consider the problem of comparing probability densities between two groups. To model the complex pattern of the underlying densities, we formulate the problem as a nonparametric density hypothesis testing problem. The major difficulty is that conventional tests may fail to distinguish the alternative from the null hypothesis under the controlled type I error. In this paper, we model log-transformed densities in a tensor product reproducing kernel Hilbert space (RKHS) and propose a probabilistic decomposition of this space. Under such a decomposition, we quantify the difference of the densities between two groups by the component norm in the probabilistic decomposition. Based on the Bernstein width, a sharp minimax lower bound of the distinguishable rate is established for the nonparametric two-sample test. We then propose a penalized likelihood ratio (PLR) test possessing the Wilks' phenomenon with an asymptotically Chi-square distributed test statistic and achieving the established minimax testing rate. Simulations and real applications demonstrate that the proposed test outperforms the conventional approaches under various scenarios.
Optimal Subsampling for Large Sample Logistic Regression
Mar 07, 2018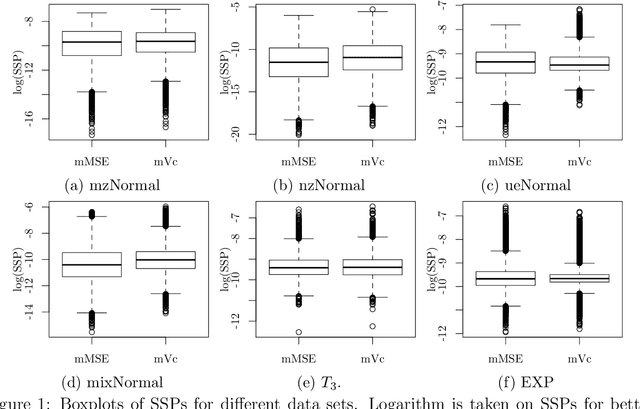
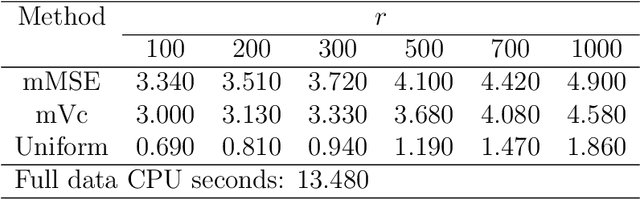
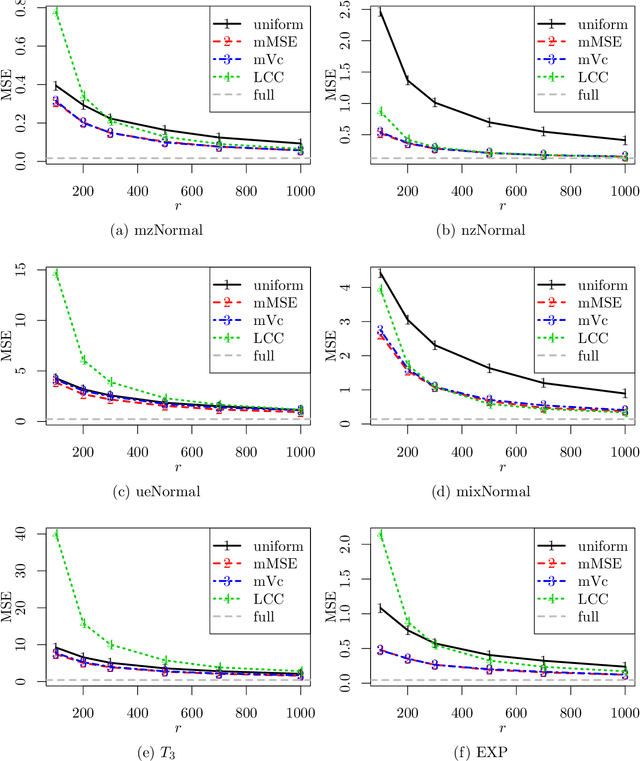
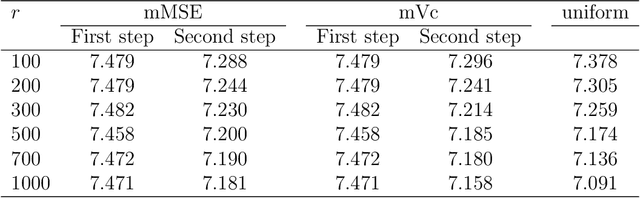
Abstract:For massive data, the family of subsampling algorithms is popular to downsize the data volume and reduce computational burden. Existing studies focus on approximating the ordinary least squares estimate in linear regression, where statistical leverage scores are often used to define subsampling probabilities. In this paper, we propose fast subsampling algorithms to efficiently approximate the maximum likelihood estimate in logistic regression. We first establish consistency and asymptotic normality of the estimator from a general subsampling algorithm, and then derive optimal subsampling probabilities that minimize the asymptotic mean squared error of the resultant estimator. An alternative minimization criterion is also proposed to further reduce the computational cost. The optimal subsampling probabilities depend on the full data estimate, so we develop a two-step algorithm to approximate the optimal subsampling procedure. This algorithm is computationally efficient and has a significant reduction in computing time compared to the full data approach. Consistency and asymptotic normality of the estimator from a two-step algorithm are also established. Synthetic and real data sets are used to evaluate the practical performance of the proposed method.
Optimal Subsampling Approaches for Large Sample Linear Regression
Nov 23, 2015Abstract:A significant hurdle for analyzing large sample data is the lack of effective statistical computing and inference methods. An emerging powerful approach for analyzing large sample data is subsampling, by which one takes a random subsample from the original full sample and uses it as a surrogate for subsequent computation and estimation. In this paper, we study subsampling methods under two scenarios: approximating the full sample ordinary least-square (OLS) estimator and estimating the coefficients in linear regression. We present two algorithms, weighted estimation algorithm and unweighted estimation algorithm, and analyze asymptotic behaviors of their resulting subsample estimators under general conditions. For the weighted estimation algorithm, we propose a criterion for selecting the optimal sampling probability by making use of the asymptotic results. On the basis of the criterion, we provide two novel subsampling methods, the optimal subsampling and the predictor- length subsampling methods. The predictor-length subsampling method is based on the L2 norm of predictors rather than leverage scores. Its computational cost is scalable. For unweighted estimation algorithm, we show that its resulting subsample estimator is not consistent to the full sample OLS estimator. However, it has better performance than the weighted estimation algorithm for estimating the coefficients. Simulation studies and a real data example are used to demonstrate the effectiveness of our proposed subsampling methods.
A Statistical Perspective on Algorithmic Leveraging
Jun 23, 2013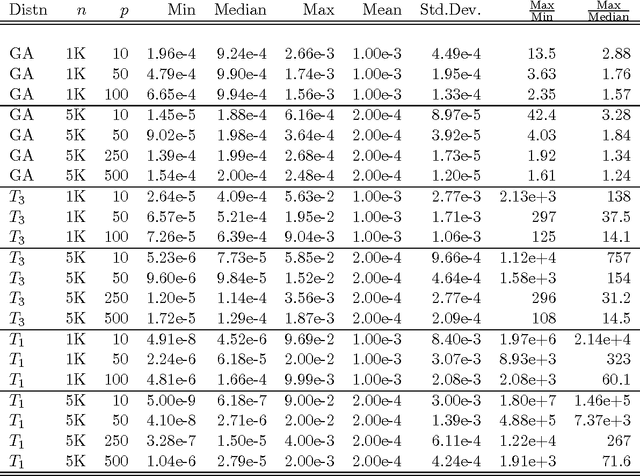
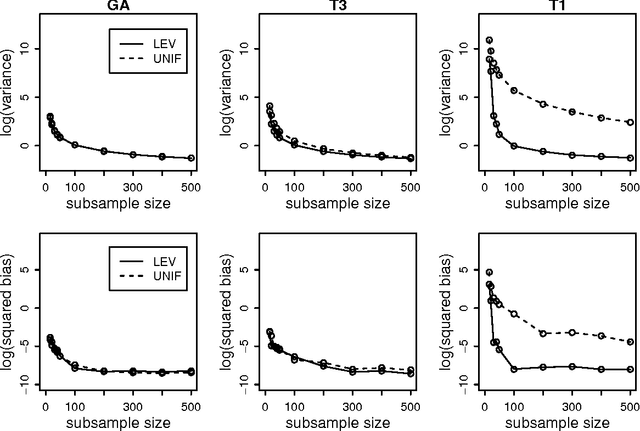
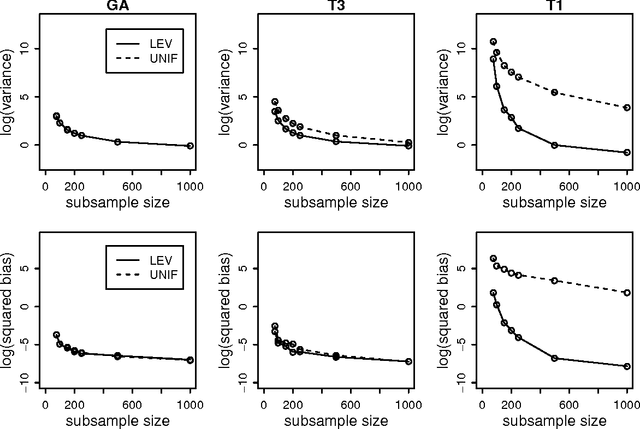
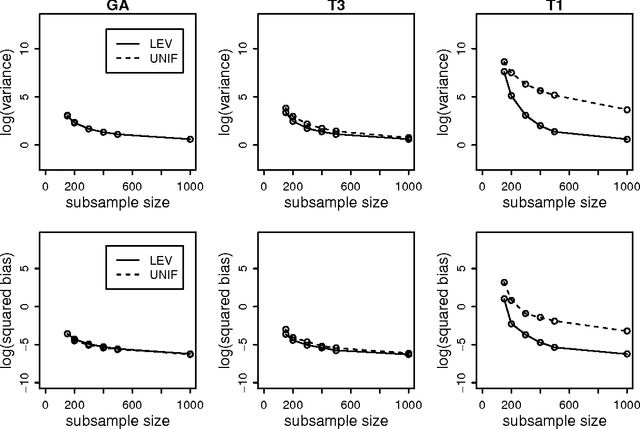
Abstract:One popular method for dealing with large-scale data sets is sampling. For example, by using the empirical statistical leverage scores as an importance sampling distribution, the method of algorithmic leveraging samples and rescales rows/columns of data matrices to reduce the data size before performing computations on the subproblem. This method has been successful in improving computational efficiency of algorithms for matrix problems such as least-squares approximation, least absolute deviations approximation, and low-rank matrix approximation. Existing work has focused on algorithmic issues such as worst-case running times and numerical issues associated with providing high-quality implementations, but none of it addresses statistical aspects of this method. In this paper, we provide a simple yet effective framework to evaluate the statistical properties of algorithmic leveraging in the context of estimating parameters in a linear regression model with a fixed number of predictors. We show that from the statistical perspective of bias and variance, neither leverage-based sampling nor uniform sampling dominates the other. This result is particularly striking, given the well-known result that, from the algorithmic perspective of worst-case analysis, leverage-based sampling provides uniformly superior worst-case algorithmic results, when compared with uniform sampling. Based on these theoretical results, we propose and analyze two new leveraging algorithms. A detailed empirical evaluation of existing leverage-based methods as well as these two new methods is carried out on both synthetic and real data sets. The empirical results indicate that our theory is a good predictor of practical performance of existing and new leverage-based algorithms and that the new algorithms achieve improved performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge