CLIMB: CLustering-based Iterative Data Mixture Bootstrapping for Language Model Pre-training

Pre-training datasets are typically collected from web content and lack inherent domain divisions. For instance, widely used datasets like Common Crawl do not include explicit domain labels, while manually curating labeled datasets such as The Pile is labor-intensive. Consequently, identifying an optimal pre-training data mixture remains a challenging problem, despite its significant benefits for pre-training performance. To address these challenges, we propose CLustering-based Iterative Data Mixture Bootstrapping (CLIMB), an automated framework that discovers, evaluates, and refines data mixtures in a pre-training setting. Specifically, CLIMB embeds and clusters large-scale datasets in a semantic space and then iteratively searches for optimal mixtures using a smaller proxy model and a predictor. When continuously trained on 400B tokens with this mixture, our 1B model exceeds the state-of-the-art Llama-3.2-1B by 2.0%. Moreover, we observe that optimizing for a specific domain (e.g., Social Sciences) yields a 5% improvement over random sampling. Finally, we introduce ClimbLab, a filtered 1.2-trillion-token corpus with 20 clusters as a research playground, and ClimbMix, a compact yet powerful 400-billion-token dataset designed for efficient pre-training that delivers superior performance under an equal token budget. We analyze the final data mixture, elucidating the characteristics of an optimal data mixture. Our data is available at: https://research.nvidia.com/labs/lpr/climb/

Text Compression for Efficient Language Generation

We challenge the prevailing assumption that LLMs must rely fully on sub-word tokens for high-quality text generation. To this end, we propose the "Generative Pretrained Thoughtformer" (GPTHF), a hierarchical transformer language model capable of text generation by compressing text into sentence embeddings and employing a sentence attention mechanism. GPTHF retains GPT's architecture, modifying only token interactions via dynamic sparse attention masks. Our experiments show that GPTHF achieves an up to an order of magnitude improvement in FLOPs efficiency and a threefold increase in runtime speed compared to equally-sized GPT models in the low-size regime. This is achieved through a unique generation method that caches and reuses sentence embeddings, allowing significant portions of the input to bypass large parts of the network.

Tiny Transformers Excel at Sentence Compression

It is staggering that words of the English language, which are on average represented by 5--6 bytes of ASCII, require as much as 24 kilobytes when served to large language models. We show that there is room for more information in every token embedding. We demonstrate that 1--3-layer transformers are capable of encoding and subsequently decoding standard English sentences into as little as a single 3-kilobyte token. Our work implies that even small networks can learn to construct valid English sentences and suggests the possibility of optimising large language models by moving from sub-word token embeddings towards larger fragments of text.

Exponentially Faster Language Modelling

Language models only really need to use an exponential fraction of their neurons for individual inferences. As proof, we present UltraFastBERT, a BERT variant that uses 0.3% of its neurons during inference while performing on par with similar BERT models. UltraFastBERT selectively engages just 12 out of 4095 neurons for each layer inference. This is achieved by replacing feedforward networks with fast feedforward networks (FFFs). While no truly efficient implementation currently exists to unlock the full acceleration potential of conditional neural execution, we provide high-level CPU code achieving 78x speedup over the optimized baseline feedforward implementation, and a PyTorch implementation delivering 40x speedup over the equivalent batched feedforward inference. We publish our training code, benchmarking setup, and model weights.

Fast Feedforward Networks

We break the linear link between the layer size and its inference cost by introducing the fast feedforward (FFF) architecture, a logarithmic-time alternative to feedforward networks. We show that FFFs give comparable performance to feedforward networks at an exponential fraction of their inference cost, are quicker to deliver performance compared to mixture-of-expert networks, and can readily take the place of either in transformers. Pushing FFFs to the absolute limit, we train a vision transformer to perform single-neuron inferences at the cost of only 5.8% performance decrease against the full-width variant. Our implementation is available as a Python package; just use "pip install fastfeedforward".

Examining the Emergence of Deductive Reasoning in Generative Language Models

We conduct a preliminary inquiry into the ability of generative transformer models to deductively reason from premises provided. We observe notable differences in the performance of models coming from different training setups and find that the deductive reasoning ability increases with scale. Further, we discover that the performance generally does not decrease with the length of the deductive chain needed to reach the conclusion, with the exception of OpenAI GPT-3 and GPT-3.5 models. Our study considers a wide variety of transformer-decoder models, ranging from 117 million to 175 billion parameters in size.

Neural Combinatorial Logic Circuit Synthesis from Input-Output Examples

We propose a novel, fully explainable neural approach to synthesis of combinatorial logic circuits from input-output examples. The carrying advantage of our method is that it readily extends to inductive scenarios, where the set of examples is incomplete but still indicative of the desired behaviour. Our method can be employed for a virtually arbitrary choice of atoms - from logic gates to FPGA blocks - as long as they can be formulated in a differentiable fashion, and consistently yields good results for synthesis of practical circuits of increasing size. In particular, we succeed in learning a number of arithmetic, bitwise, and signal-routing operations, and even generalise towards the correct behaviour in inductive scenarios. Our method, attacking a discrete logical synthesis problem with an explainable neural approach, hints at a wider promise for synthesis and reasoning-related tasks.

Deterministic Graph-Walking Program Mining

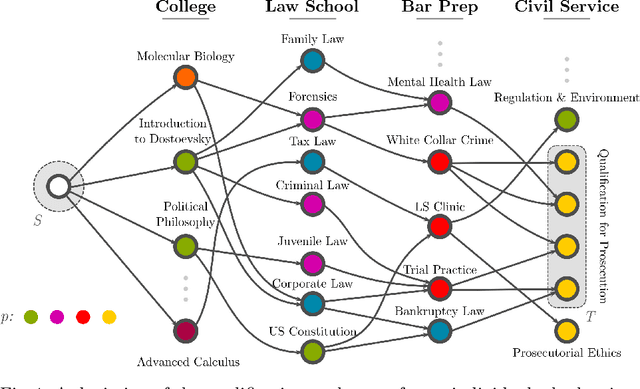
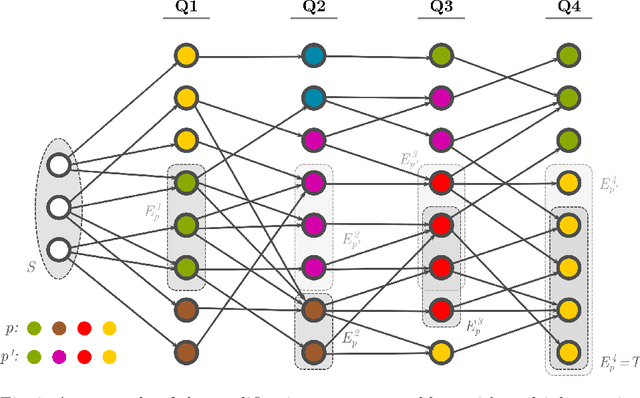
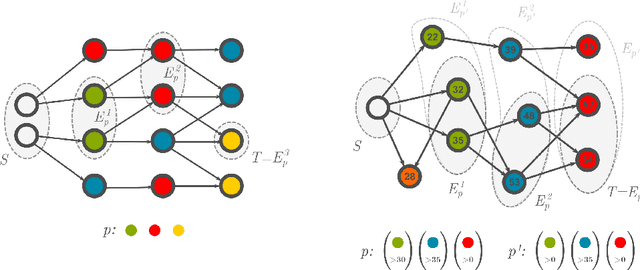
Owing to their versatility, graph structures admit representations of intricate relationships between the separate entities comprising the data. We formalise the notion of connection between two vertex sets in terms of edge and vertex features by introducing graph-walking programs. We give two algorithms for mining of deterministic graph-walking programs that yield programs in the order of increasing length. These programs characterise linear long-distance relationships between the given two vertex sets in the context of the whole graph.

The LL strategy for optimal LL parsing

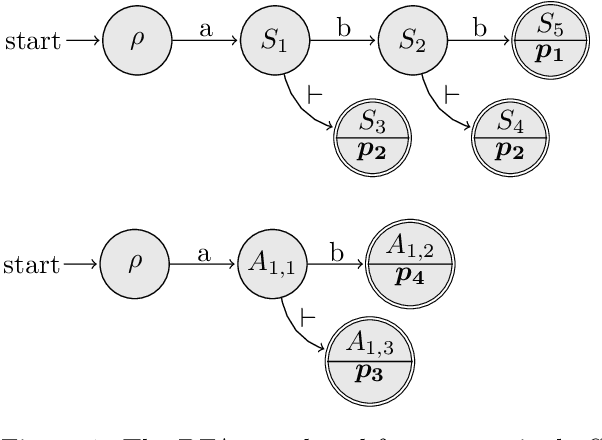
The LL(finite) parsing strategy for parsing of LL(k) grammars where k needs not to be known is presented. The strategy parses input in linear time, uses arbitrary but always minimal lookahead necessary to disambiguate between alternatives of nonterminals, and it is optimal in the number of lookahead terminal scans performed. Modifications to the algorithm are shown that allow for resolution of grammar ambiguities by precedence -- effectively interpreting the input as a parsing expression grammar -- as well as for the use of predicates, and a proof of concept, the open-source parser generator Astir, employs the LL(finite) strategy in the output it generates.