LegalLens Shared Task 2024: Legal Violation Identification in Unstructured Text

This paper presents the results of the LegalLens Shared Task, focusing on detecting legal violations within text in the wild across two sub-tasks: LegalLens-NER for identifying legal violation entities and LegalLens-NLI for associating these violations with relevant legal contexts and affected individuals. Using an enhanced LegalLens dataset covering labor, privacy, and consumer protection domains, 38 teams participated in the task. Our analysis reveals that while a mix of approaches was used, the top-performing teams in both tasks consistently relied on fine-tuning pre-trained language models, outperforming legal-specific models and few-shot methods. The top-performing team achieved a 7.11% improvement in NER over the baseline, while NLI saw a more marginal improvement of 5.7%. Despite these gains, the complexity of legal texts leaves room for further advancements.

Report Cards: Qualitative Evaluation of Language Models Using Natural Language Summaries

The rapid development and dynamic nature of large language models (LLMs) make it difficult for conventional quantitative benchmarks to accurately assess their capabilities. We propose report cards, which are human-interpretable, natural language summaries of model behavior for specific skills or topics. We develop a framework to evaluate report cards based on three criteria: specificity (ability to distinguish between models), faithfulness (accurate representation of model capabilities), and interpretability (clarity and relevance to humans). We also propose an iterative algorithm for generating report cards without human supervision and explore its efficacy by ablating various design choices. Through experimentation with popular LLMs, we demonstrate that report cards provide insights beyond traditional benchmarks and can help address the need for a more interpretable and holistic evaluation of LLMs.

Reward Machines for Deep RL in Noisy and Uncertain Environments

Reward Machines provide an automata-inspired structure for specifying instructions, safety constraints, and other temporally extended reward-worthy behaviour. By exposing complex reward function structure, they enable counterfactual learning updates that have resulted in impressive sample efficiency gains. While Reward Machines have been employed in both tabular and deep RL settings, they have typically relied on a ground-truth interpretation of the domain-specific vocabulary that form the building blocks of the reward function. Such ground-truth interpretations can be elusive in many real-world settings, due in part to partial observability or noisy sensing. In this paper, we explore the use of Reward Machines for Deep RL in noisy and uncertain environments. We characterize this problem as a POMDP and propose a suite of RL algorithms that leverage task structure under uncertain interpretation of domain-specific vocabulary. Theoretical analysis exposes pitfalls in naive approaches to this problem, while experimental results show that our algorithms successfully leverage task structure to improve performance under noisy interpretations of the vocabulary. Our results provide a general framework for exploiting Reward Machines in partially observable environments.

Fast Matrix Multiplication Without Tears: A Constraint Programming Approach

It is known that the multiplication of an $N \times M$ matrix with an $M \times P$ matrix can be performed using fewer multiplications than what the naive $NMP$ approach suggests. The most famous instance of this is Strassen's algorithm for multiplying two $2\times 2$ matrices in 7 instead of 8 multiplications. This gives rise to the constraint satisfaction problem of fast matrix multiplication, where a set of $R < NMP$ multiplication terms must be chosen and combined such that they satisfy correctness constraints on the output matrix. Despite its highly combinatorial nature, this problem has not been exhaustively examined from that perspective, as evidenced for example by the recent deep reinforcement learning approach of AlphaTensor. In this work, we propose a simple yet novel Constraint Programming approach to find non-commutative algorithms for fast matrix multiplication or provide proof of infeasibility otherwise. We propose a set of symmetry-breaking constraints and valid inequalities that are particularly helpful in proving infeasibility. On the feasible side, we find that exploiting solver performance variability in conjunction with a sparsity-based problem decomposition enables finding solutions for larger (feasible) instances of fast matrix multiplication. Our experimental results using CP Optimizer demonstrate that we can find fast matrix multiplication algorithms for matrices up to $3\times 3$ in a short amount of time.

LLMs and the Abstraction and Reasoning Corpus: Successes, Failures, and the Importance of Object-based Representations

Can a Large Language Model (LLM) solve simple abstract reasoning problems? We explore this broad question through a systematic analysis of GPT on the Abstraction and Reasoning Corpus (ARC), a representative benchmark of abstract reasoning ability from limited examples in which solutions require some "core knowledge" of concepts such as objects, goal states, counting, and basic geometry. GPT-4 solves only 13/50 of the most straightforward ARC tasks when using textual encodings for their two-dimensional input-output grids. Our failure analysis reveals that GPT-4's capacity to identify objects and reason about them is significantly influenced by the sequential nature of the text that represents an object within a text encoding of a task. To test this hypothesis, we design a new benchmark, the 1D-ARC, which consists of one-dimensional (array-like) tasks that are more conducive to GPT-based reasoning, and where it indeed performs better than on the (2D) ARC. To alleviate this issue, we propose an object-based representation that is obtained through an external tool, resulting in nearly doubling the performance on solved ARC tasks and near-perfect scores on the easier 1D-ARC. Although the state-of-the-art GPT-4 is unable to "reason" perfectly within non-language domains such as the 1D-ARC or a simple ARC subset, our study reveals that the use of object-based representations can significantly improve its reasoning ability. Visualizations, GPT logs, and data are available at https://khalil-research.github.io/LLM4ARC.

Noisy Symbolic Abstractions for Deep RL: A case study with Reward Machines

Natural and formal languages provide an effective mechanism for humans to specify instructions and reward functions. We investigate how to generate policies via RL when reward functions are specified in a symbolic language captured by Reward Machines, an increasingly popular automaton-inspired structure. We are interested in the case where the mapping of environment state to a symbolic (here, Reward Machine) vocabulary -- commonly known as the labelling function -- is uncertain from the perspective of the agent. We formulate the problem of policy learning in Reward Machines with noisy symbolic abstractions as a special class of POMDP optimization problem, and investigate several methods to address the problem, building on existing and new techniques, the latter focused on predicting Reward Machine state, rather than on grounding of individual symbols. We analyze these methods and evaluate them experimentally under varying degrees of uncertainty in the correct interpretation of the symbolic vocabulary. We verify the strength of our approach and the limitation of existing methods via an empirical investigation on both illustrative, toy domains and partially observable, deep RL domains.

Learning to Follow Instructions in Text-Based Games

Text-based games present a unique class of sequential decision making problem in which agents interact with a partially observable, simulated environment via actions and observations conveyed through natural language. Such observations typically include instructions that, in a reinforcement learning (RL) setting, can directly or indirectly guide a player towards completing reward-worthy tasks. In this work, we study the ability of RL agents to follow such instructions. We conduct experiments that show that the performance of state-of-the-art text-based game agents is largely unaffected by the presence or absence of such instructions, and that these agents are typically unable to execute tasks to completion. To further study and address the task of instruction following, we equip RL agents with an internal structured representation of natural language instructions in the form of Linear Temporal Logic (LTL), a formal language that is increasingly used for temporally extended reward specification in RL. Our framework both supports and highlights the benefit of understanding the temporal semantics of instructions and in measuring progress towards achievement of such a temporally extended behaviour. Experiments with 500+ games in TextWorld demonstrate the superior performance of our approach.

Challenges to Solving Combinatorially Hard Long-Horizon Deep RL Tasks

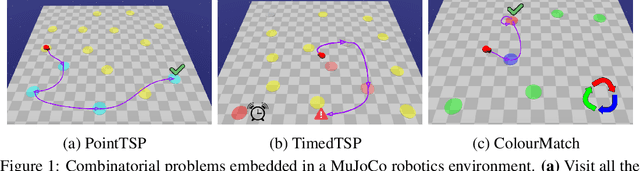
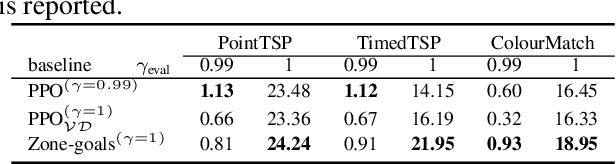
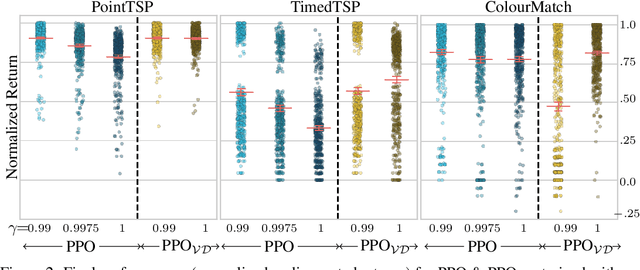
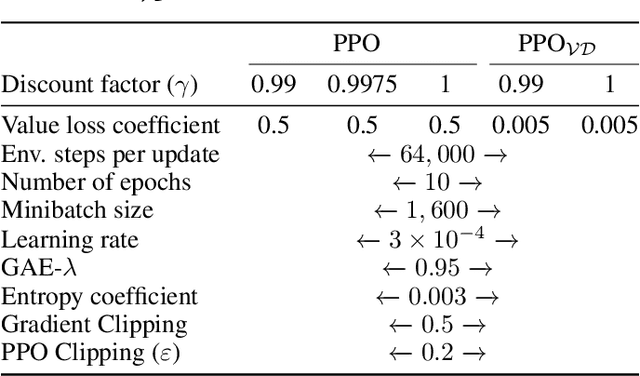
Deep reinforcement learning has shown promise in discrete domains requiring complex reasoning, including games such as Chess, Go, and Hanabi. However, this type of reasoning is less often observed in long-horizon, continuous domains with high-dimensional observations, where instead RL research has predominantly focused on problems with simple high-level structure (e.g. opening a drawer or moving a robot as fast as possible). Inspired by combinatorially hard optimization problems, we propose a set of robotics tasks which admit many distinct solutions at the high-level, but require reasoning about states and rewards thousands of steps into the future for the best performance. Critically, while RL has traditionally suffered on complex, long-horizon tasks due to sparse rewards, our tasks are carefully designed to be solvable without specialized exploration. Nevertheless, our investigation finds that standard RL methods often neglect long-term effects due to discounting, while general-purpose hierarchical RL approaches struggle unless additional abstract domain knowledge can be exploited.

Augment with Care: Contrastive Learning for the Boolean Satisfiability Problem

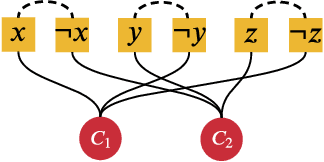
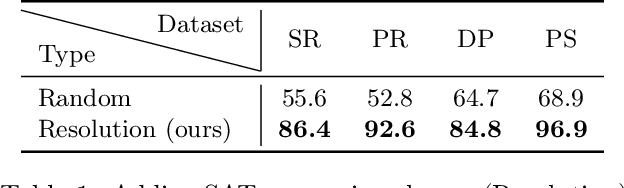
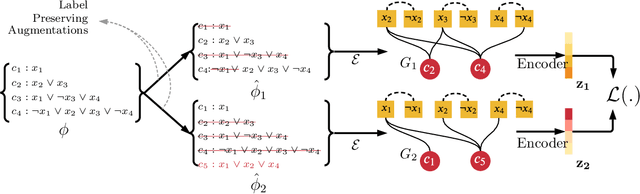
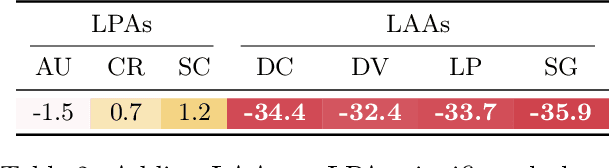
Supervised learning can improve the design of state-of-the-art solvers for combinatorial problems, but labelling large numbers of combinatorial instances is often impractical due to exponential worst-case complexity. Inspired by the recent success of contrastive pre-training for images, we conduct a scientific study of the effect of augmentation design on contrastive pre-training for the Boolean satisfiability problem. While typical graph contrastive pre-training uses label-agnostic augmentations, our key insight is that many combinatorial problems have well-studied invariances, which allow for the design of label-preserving augmentations. We find that label-preserving augmentations are critical for the success of contrastive pre-training. We show that our representations are able to achieve comparable test accuracy to fully-supervised learning while using only 1% of the labels. We also demonstrate that our representations are more transferable to larger problems from unseen domains.

Finding Backdoors to Integer Programs: A Monte Carlo Tree Search Framework

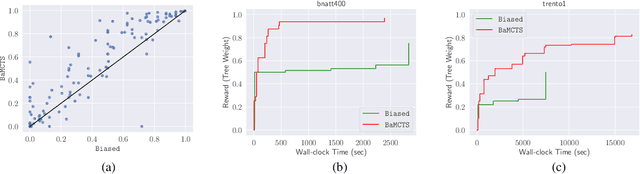
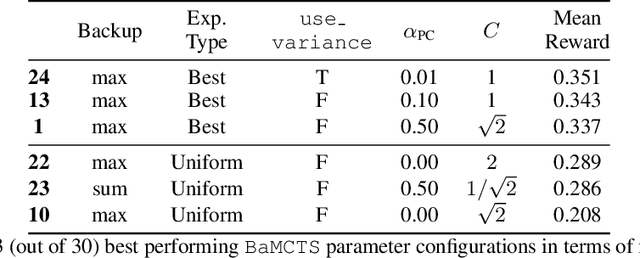
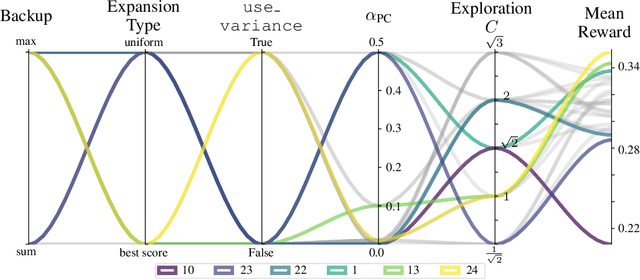
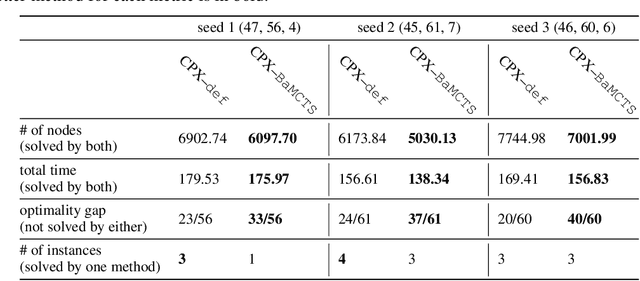
In Mixed Integer Linear Programming (MIP), a (strong) backdoor is a "small" subset of an instance's integer variables with the following property: in a branch-and-bound procedure, the instance can be solved to global optimality by branching only on the variables in the backdoor. Constructing datasets of pre-computed backdoors for widely used MIP benchmark sets or particular problem families can enable new questions around novel structural properties of a MIP, or explain why a problem that is hard in theory can be solved efficiently in practice. Existing algorithms for finding backdoors rely on sampling candidate variable subsets in various ways, an approach which has demonstrated the existence of backdoors for some instances from MIPLIB2003 and MIPLIB2010. However, these algorithms fall short of consistently succeeding at the task due to an imbalance between exploration and exploitation. We propose BaMCTS, a Monte Carlo Tree Search framework for finding backdoors to MIPs. Extensive algorithmic engineering, hybridization with traditional MIP concepts, and close integration with the CPLEX solver have enabled our method to outperform baselines on MIPLIB2017 instances, finding backdoors more frequently and more efficiently.