Learned iterative networks: An operator learning perspective

Learned image reconstruction has become a pillar in computational imaging and inverse problems. Among the most successful approaches are learned iterative networks, which are formulated by unrolling classical iterative optimisation algorithms for solving variational problems. While the underlying algorithm is usually formulated in the functional analytic setting, learned approaches are often viewed as purely discrete. In this chapter we present a unified operator view for learned iterative networks. Specifically, we formulate a learned reconstruction operator, defining how to compute, and separately the learning problem, which defines what to compute. In this setting we present common approaches and show that many approaches are closely related in their core. We review linear as well as nonlinear inverse problems in this framework and present a short numerical study to conclude.

Improving the Generalisation of Learned Reconstruction Frameworks

Ensuring proper generalization is a critical challenge in applying data-driven methods for solving inverse problems in imaging, as neural networks reconstructing an image must perform well across varied datasets and acquisition geometries. In X-ray Computed Tomography (CT), convolutional neural networks (CNNs) are widely used to filter the projection data but are ill-suited for this task as they apply grid-based convolutions to the sinogram, which inherently lies on a line manifold, not a regular grid. The CNNs, unaware of the geometry, are implicitly tied to it and require an excessive amount of parameters as they must infer the relations between measurements from the data rather than from prior information. The contribution of this paper is twofold. First, we introduce a graph data structure to represent CT acquisition geometries and tomographic data, providing a detailed explanation of the graph's structure for circular, cone-beam geometries. Second, we propose GLM, a hybrid neural network architecture that leverages both graph and grid convolutions to process tomographic data. We demonstrate that GLM outperforms CNNs when performance is quantified in terms of structural similarity and peak signal-to-noise ratio, despite the fact that GLM uses only a fraction of the trainable parameters. Compared to CNNs, GLM also requires significantly less training time and memory, and its memory requirements scale better. Crucially, GLM demonstrates robust generalization to unseen variations in the acquisition geometry, like when training only on fully sampled CT data and then testing on sparse-view CT data.

Self-Supervised Denoiser Framework

Reconstructing images using Computed Tomography (CT) in an industrial context leads to specific challenges that differ from those encountered in other areas, such as clinical CT. Indeed, non-destructive testing with industrial CT will often involve scanning multiple similar objects while maintaining high throughput, requiring short scanning times, which is not a relevant concern in clinical CT. Under-sampling the tomographic data (sinograms) is a natural way to reduce the scanning time at the cost of image quality since the latter depends on the number of measurements. In such a scenario, post-processing techniques are required to compensate for the image artifacts induced by the sinogram sparsity. We introduce the Self-supervised Denoiser Framework (SDF), a self-supervised training method that leverages pre-training on highly sampled sinogram data to enhance the quality of images reconstructed from undersampled sinogram data. The main contribution of SDF is that it proposes to train an image denoiser in the sinogram space by setting the learning task as the prediction of one sinogram subset from another. As such, it does not require ground-truth image data, leverages the abundant data modality in CT, the sinogram, and can drastically enhance the quality of images reconstructed from a fraction of the measurements. We demonstrate that SDF produces better image quality, in terms of peak signal-to-noise ratio, than other analytical and self-supervised frameworks in both 2D fan-beam or 3D cone-beam CT settings. Moreover, we show that the enhancement provided by SDF carries over when fine-tuning the image denoiser on a few examples, making it a suitable pre-training technique in a context where there is little high-quality image data. Our results are established on experimental datasets, making SDF a strong candidate for being the building block of foundational image-enhancement models in CT.

Pullback Flow Matching on Data Manifolds

We propose Pullback Flow Matching (PFM), a novel framework for generative modeling on data manifolds. Unlike existing methods that assume or learn restrictive closed-form manifold mappings for training Riemannian Flow Matching (RFM) models, PFM leverages pullback geometry and isometric learning to preserve the underlying manifold's geometry while enabling efficient generation and precise interpolation in latent space. This approach not only facilitates closed-form mappings on the data manifold but also allows for designable latent spaces, using assumed metrics on both data and latent manifolds. By enhancing isometric learning through Neural ODEs and proposing a scalable training objective, we achieve a latent space more suitable for interpolation, leading to improved manifold learning and generative performance. We demonstrate PFM's effectiveness through applications in synthetic data, protein dynamics and protein sequence data, generating novel proteins with specific properties. This method shows strong potential for drug discovery and materials science, where generating novel samples with specific properties is of great interest.

Reconstruction for Sparse View Tomography of Long Objects Applied to Imaging in the Wood Industry

In the wood industry, logs are commonly quality screened by discrete X-ray scans on a moving conveyor belt from a few source positions. Typically, two-dimensional (2D) slice-wise measurements are obtained by a sequential scanning geometry. Each 2D slice alone does not carry sufficient information for a three-dimensional tomographic reconstruction in which biological features of interest in the log are well preserved. In the present work, we propose a learned iterative reconstruction method based on the Learned Primal-Dual neural network, suited for sequential scanning geometries. Our method accumulates information between neighbouring slices, instead of only accounting for single slices during reconstruction. Our quantitative and qualitative evaluations with as few as five source positions show that our method yields reconstructions of logs that are sufficiently accurate to identify biological features like knots (branches), heartwood and sapwood.

Neural incomplete factorization: learning preconditioners for the conjugate gradient method

In this paper, we develop a novel data-driven approach to accelerate solving large-scale linear equation systems encountered in scientific computing and optimization. Our method utilizes self-supervised training of a graph neural network to generate an effective preconditioner tailored to the specific problem domain. By replacing conventional hand-crafted preconditioners used with the conjugate gradient method, our approach, named neural incomplete factorization (NeuralIF), significantly speeds-up convergence and computational efficiency. At the core of our method is a novel message-passing block, inspired by sparse matrix theory, that aligns with the objective to find a sparse factorization of the matrix. We evaluate our proposed method on both a synthetic and a real-world problem arising from scientific computing. Our results demonstrate that NeuralIF consistently outperforms the most common general-purpose preconditioners, including the incomplete Cholesky method, achieving competitive performance across various metrics even outside the training data distribution.

Calibrating Ensembles for Scalable Uncertainty Quantification in Deep Learning-based Medical Segmentation

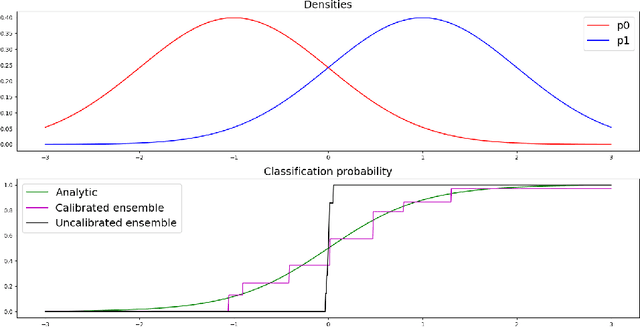
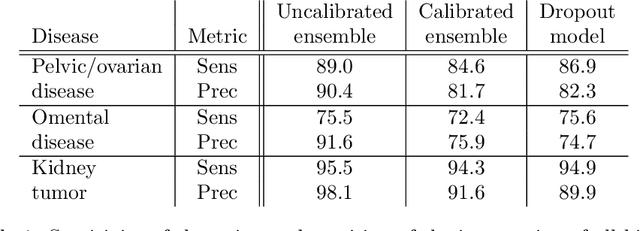
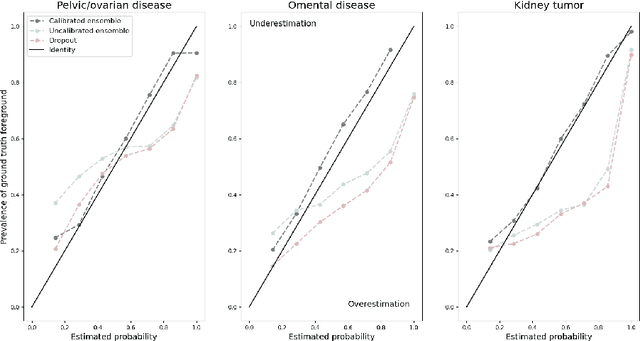
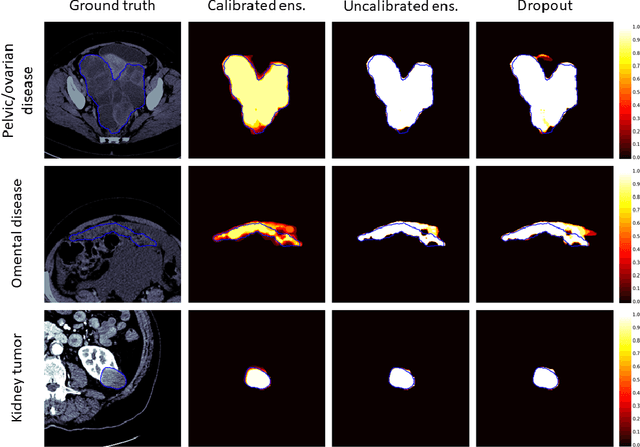
Uncertainty quantification in automated image analysis is highly desired in many applications. Typically, machine learning models in classification or segmentation are only developed to provide binary answers; however, quantifying the uncertainty of the models can play a critical role for example in active learning or machine human interaction. Uncertainty quantification is especially difficult when using deep learning-based models, which are the state-of-the-art in many imaging applications. The current uncertainty quantification approaches do not scale well in high-dimensional real-world problems. Scalable solutions often rely on classical techniques, such as dropout, during inference or training ensembles of identical models with different random seeds to obtain a posterior distribution. In this paper, we show that these approaches fail to approximate the classification probability. On the contrary, we propose a scalable and intuitive framework to calibrate ensembles of deep learning models to produce uncertainty quantification measurements that approximate the classification probability. On unseen test data, we demonstrate improved calibration, sensitivity (in two out of three cases) and precision when being compared with the standard approaches. We further motivate the usage of our method in active learning, creating pseudo-labels to learn from unlabeled images and human-machine collaboration.

Spectral decomposition of atomic structures in heterogeneous cryo-EM

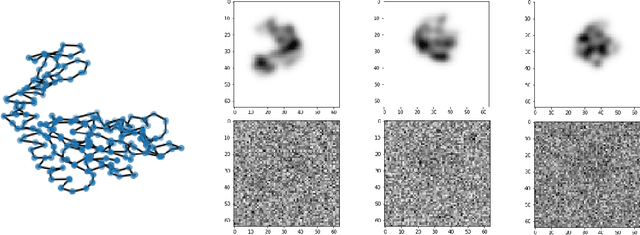
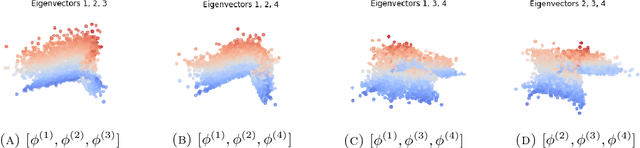
We consider the problem of recovering the three-dimensional atomic structure of a flexible macromolecule from a heterogeneous cryo-EM dataset. The dataset contains noisy tomographic projections of the electrostatic potential of the macromolecule, taken from different viewing directions, and in the heterogeneous case, each image corresponds to a different conformation of the macromolecule. Under the assumption that the macromolecule can be modelled as a chain, or discrete curve (as it is for instance the case for a protein backbone with a single chain of amino-acids), we introduce a method to estimate the deformation of the atomic model with respect to a given conformation, which is assumed to be known a priori. Our method consists on estimating the torsion and bond angles of the atomic model in each conformation as a linear combination of the eigenfunctions of the Laplace operator in the manifold of conformations. These eigenfunctions can be approximated by means of a well-known technique in manifold learning, based on the construction of a graph Laplacian using the cryo-EM dataset. Finally, we test our approach with synthetic datasets, for which we recover the atomic model of two-dimensional and three-dimensional flexible structures from noisy tomographic projections.

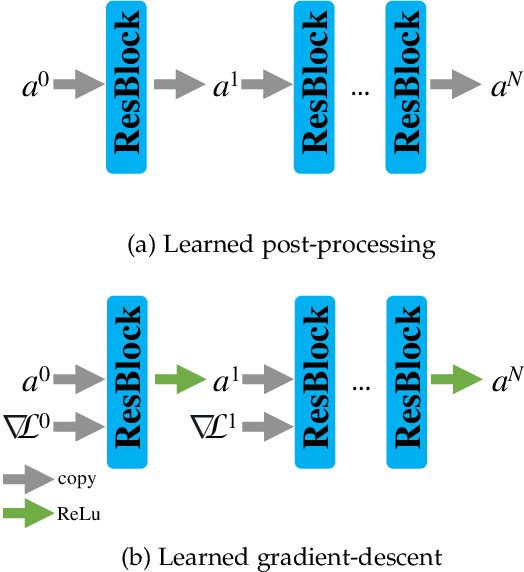
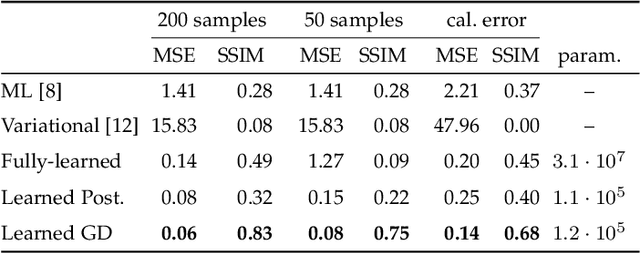
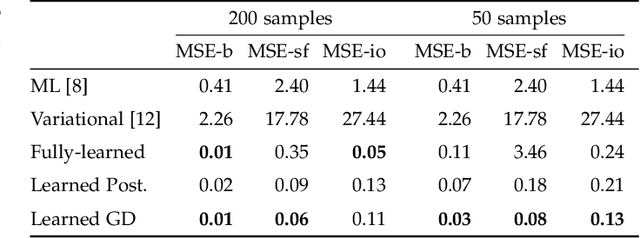
Deep Learning for Material Decomposition in Photon-Counting CT

Photon-counting CT (PCCT) offers improved diagnostic performance through better spatial and energy resolution, but developing high-quality image reconstruction methods that can deal with these large datasets is challenging. Model-based solutions incorporate models of the physical acquisition in order to reconstruct more accurate images, but are dependent on an accurate forward operator and present difficulties with finding good regularization. Another approach is deep-learning reconstruction, which has shown great promise in CT. However, fully data-driven solutions typically need large amounts of training data and lack interpretability. To combine the benefits of both methods, while minimizing their respective drawbacks, it is desirable to develop reconstruction algorithms that combine both model-based and data-driven approaches. In this work, we present a novel deep-learning solution for material decomposition in PCCT, based on an unrolled/unfolded iterative network. We evaluate two cases: a learned post-processing, which implicitly utilizes model knowledge, and a learned gradient-descent, which has explicit model-based components in the architecture. With our proposed techniques, we solve a challenging PCCT simulation case: three-material decomposition in abdomen imaging with low dose, iodine contrast, and a very small training sample support. In this scenario, our approach outperforms a maximum likelihood estimation, a variational method, as well as a fully-learned network.

Learned reconstruction with convergence guarantees

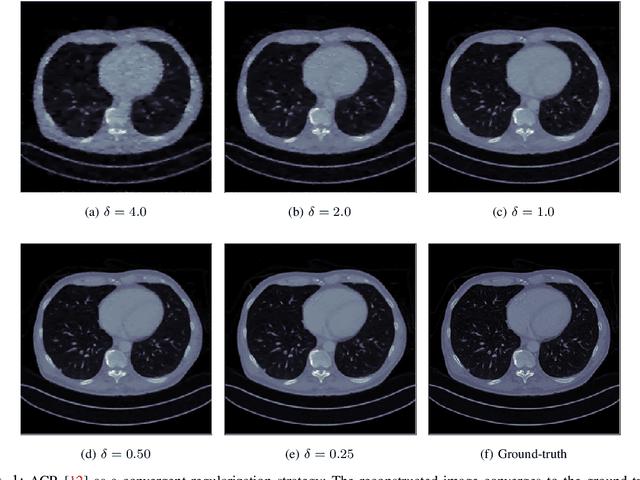
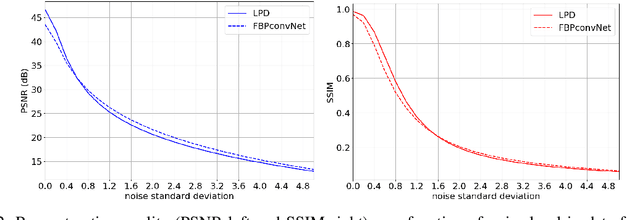
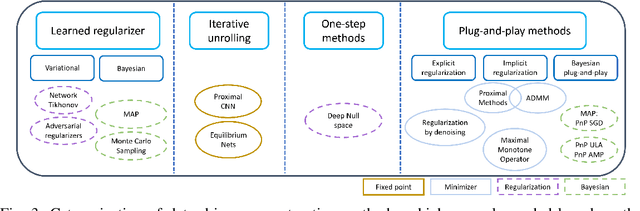
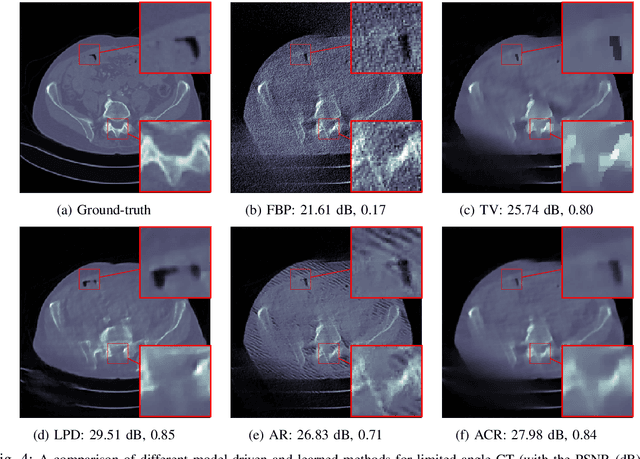
In recent years, deep learning has achieved remarkable empirical success for image reconstruction. This has catalyzed an ongoing quest for precise characterization of correctness and reliability of data-driven methods in critical use-cases, for instance in medical imaging. Notwithstanding the excellent performance and efficacy of deep learning-based methods, concerns have been raised regarding their stability, or lack thereof, with serious practical implications. Significant advances have been made in recent years to unravel the inner workings of data-driven image recovery methods, challenging their widely perceived black-box nature. In this article, we will specify relevant notions of convergence for data-driven image reconstruction, which will form the basis of a survey of learned methods with mathematically rigorous reconstruction guarantees. An example that is highlighted is the role of ICNN, offering the possibility to combine the power of deep learning with classical convex regularization theory for devising methods that are provably convergent. This survey article is aimed at both methodological researchers seeking to advance the frontiers of our understanding of data-driven image reconstruction methods as well as practitioners, by providing an accessible description of convergence concepts and by placing some of the existing empirical practices on a solid mathematical foundation.