Small Models, Smarter Learning: The Power of Joint Task Training

The ability of a model to learn a task depends strongly on both the task difficulty and the model size. We aim to understand how task difficulty relates to the minimum number of parameters required for learning specific tasks in small transformer models. Our study focuses on the ListOps dataset, which consists of nested mathematical operations. We gradually increase task difficulty by introducing new operations or combinations of operations into the training data. We observe that sum modulo n is the hardest to learn. Curiously, when combined with other operations such as maximum and median, the sum operation becomes easier to learn and requires fewer parameters. We show that joint training not only improves performance but also leads to qualitatively different model behavior. We show evidence that models trained only on SUM might be memorizing and fail to capture the number structure in the embeddings. In contrast, models trained on a mixture of SUM and other operations exhibit number-like representations in the embedding space, and a strong ability to distinguish parity. Furthermore, the SUM-only model relies more heavily on its feedforward layers, while the jointly trained model activates the attention mechanism more. Finally, we show that learning pure SUM can be induced in models below the learning threshold of pure SUM, by pretraining them on MAX+MED. Our findings indicate that emergent abilities in language models depend not only on model size, but also the training curriculum.

Faster Optimization on Sparse Graphs via Neural Reparametrization

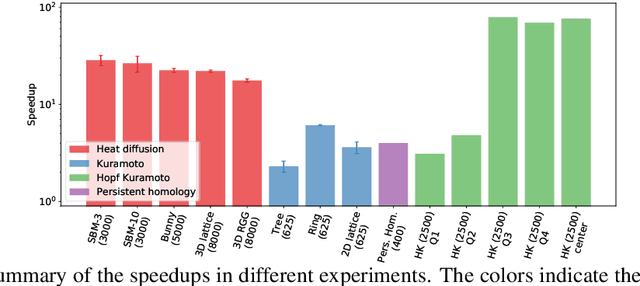
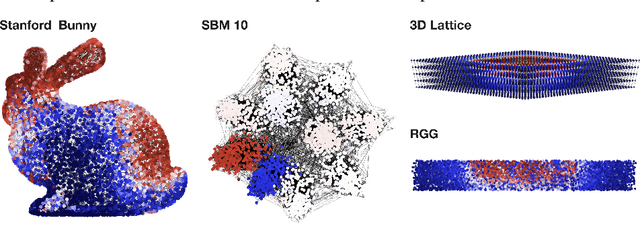
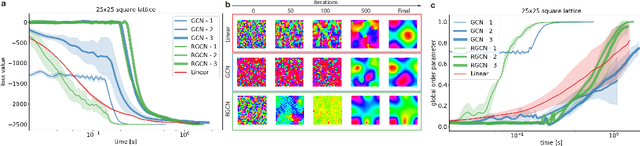
In mathematical optimization, second-order Newton's methods generally converge faster than first-order methods, but they require the inverse of the Hessian, hence are computationally expensive. However, we discover that on sparse graphs, graph neural networks (GNN) can implement an efficient Quasi-Newton method that can speed up optimization by a factor of 10-100x. Our method, neural reparametrization, modifies the optimization parameters as the output of a GNN to reshape the optimization landscape. Using a precomputed Hessian as the propagation rule, the GNN can effectively utilize the second-order information, reaching a similar effect as adaptive gradient methods. As our method solves optimization through architecture design, it can be used in conjunction with any optimizers such as Adam and RMSProp. We show the application of our method on scientifically relevant problems including heat diffusion, synchronization and persistent homology.