Fused Gromov-Wasserstein distance for structured objects: theoretical foundations and mathematical properties

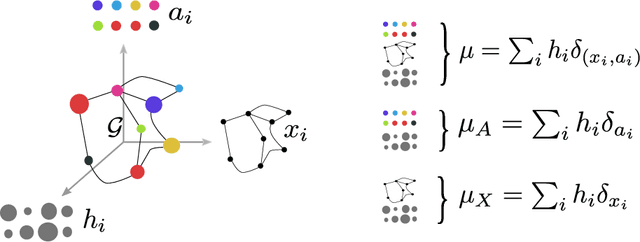
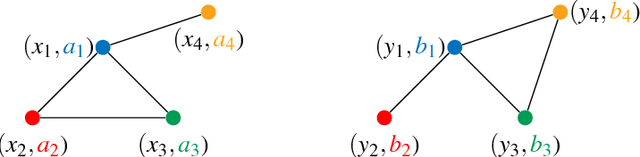
Optimal transport theory has recently found many applications in machine learning thanks to its capacity for comparing various machine learning objects considered as distributions. The Kantorovitch formulation, leading to the Wasserstein distance, focuses on the features of the elements of the objects but treat them independently, whereas the Gromov-Wasserstein distance focuses only on the relations between the elements, depicting the structure of the object, yet discarding its features. In this paper we propose to extend these distances in order to encode simultaneously both the feature and structure informations, resulting in the Fused Gromov-Wasserstein distance. We develop the mathematical framework for this novel distance, prove its metric and interpolation properties and provide a concentration result for the convergence of finite samples. We also illustrate and interpret its use in various contexts where structured objects are involved.

An Entropic Optimal Transport Loss for Learning Deep Neural Networks under Label Noise in Remote Sensing Images

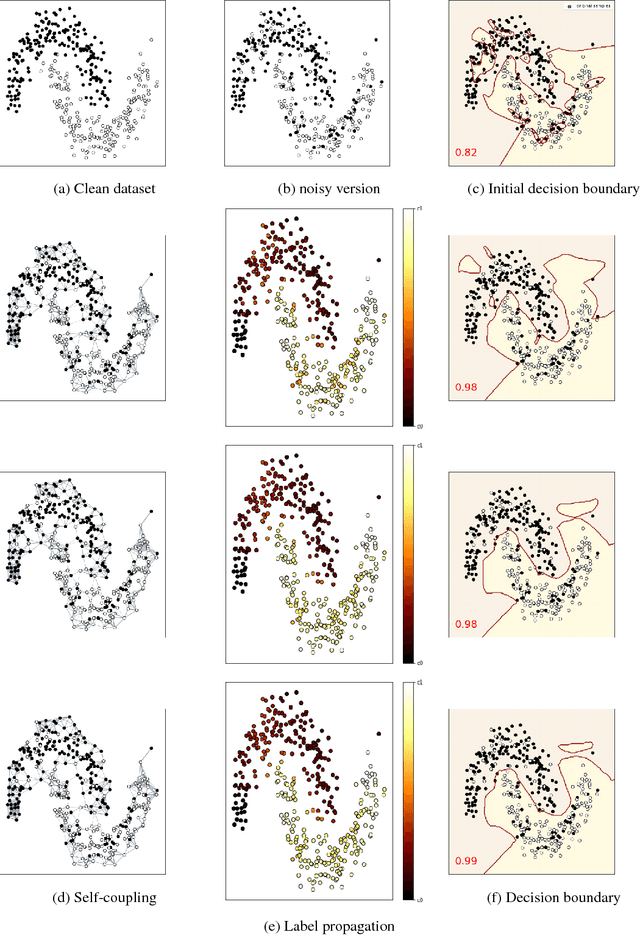
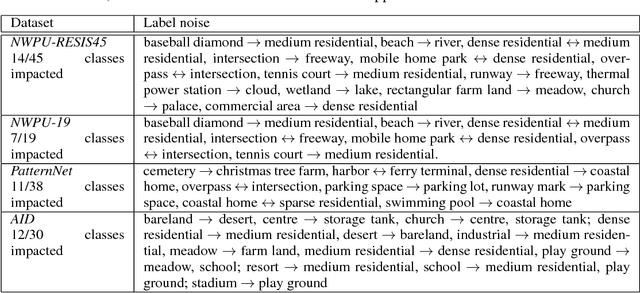
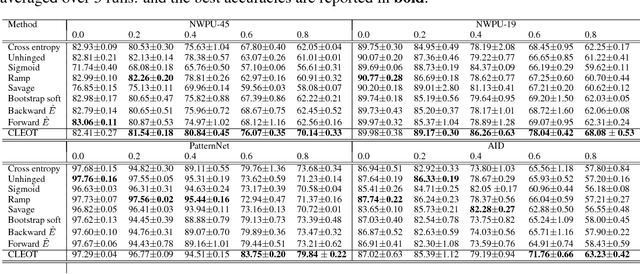
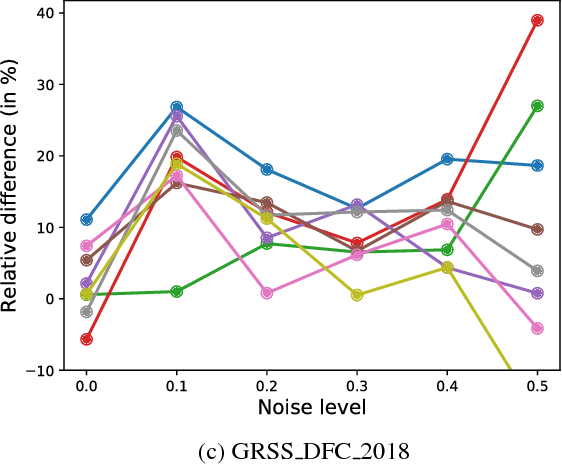
Deep neural networks have established as a powerful tool for large scale supervised classification tasks. The state-of-the-art performances of deep neural networks are conditioned to the availability of large number of accurately labeled samples. In practice, collecting large scale accurately labeled datasets is a challenging and tedious task in most scenarios of remote sensing image analysis, thus cheap surrogate procedures are employed to label the dataset. Training deep neural networks on such datasets with inaccurate labels easily overfits to the noisy training labels and degrades the performance of the classification tasks drastically. To mitigate this effect, we propose an original solution with entropic optimal transportation. It allows to learn in an end-to-end fashion deep neural networks that are, to some extent, robust to inaccurately labeled samples. We empirically demonstrate on several remote sensing datasets, where both scene and pixel-based hyperspectral images are considered for classification. Our method proves to be highly tolerant to significant amounts of label noise and achieves favorable results against state-of-the-art methods.

DeepJDOT: Deep Joint Distribution Optimal Transport for Unsupervised Domain Adaptation

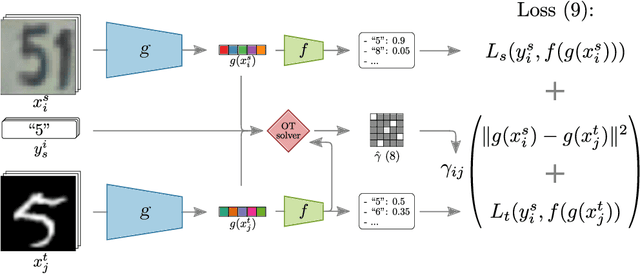
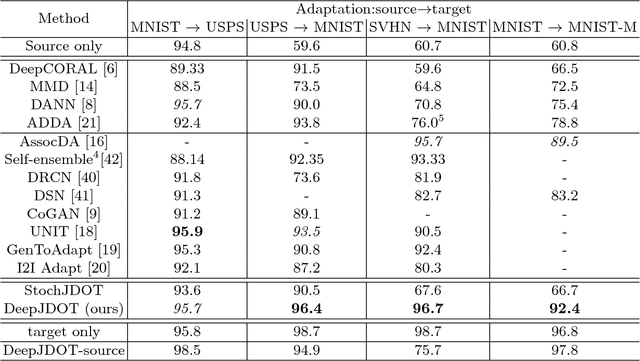
In computer vision, one is often confronted with problems of domain shifts, which occur when one applies a classifier trained on a source dataset to target data sharing similar characteristics (e.g. same classes), but also different latent data structures (e.g. different acquisition conditions). In such a situation, the model will perform poorly on the new data, since the classifier is specialized to recognize visual cues specific to the source domain. In this work we explore a solution, named DeepJDOT, to tackle this problem: through a measure of discrepancy on joint deep representations/labels based on optimal transport, we not only learn new data representations aligned between the source and target domain, but also simultaneously preserve the discriminative information used by the classifier. We applied DeepJDOT to a series of visual recognition tasks, where it compares favorably against state-of-the-art deep domain adaptation methods.

Optimal Transport for structured data

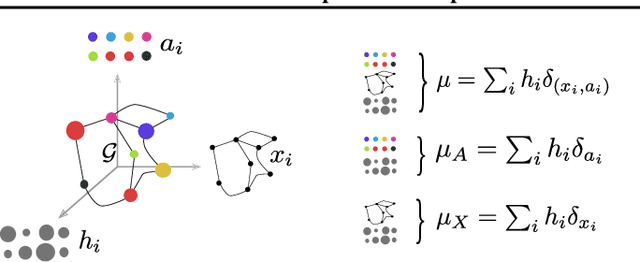
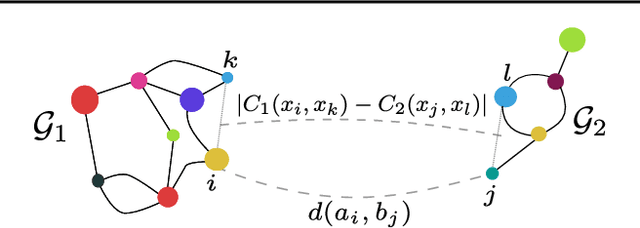
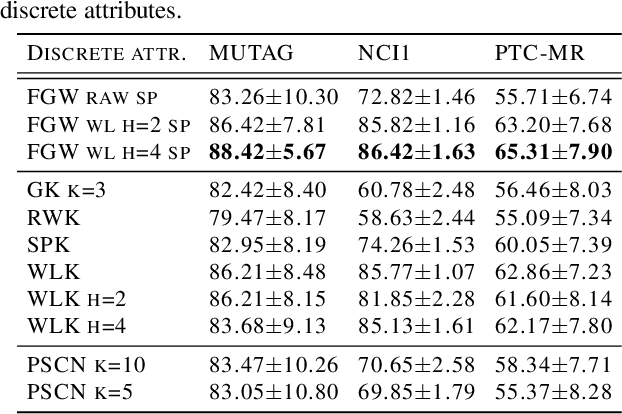
Optimal transport has recently gained a lot of interest in the machine learning community thanks to its ability to compare probability distributions while respecting the underlying space's geometry. Wasserstein distance deals with feature information through its metric or cost function, but fails in exploiting the structural information, i.e the specific relations existing among the components of the distribution. Recently adapted to a machine learning context, the Gromov-Wasserstein distance defines a metric well suited for comparing distributions that live in different metric spaces by exploiting their inner structural information. In this paper we propose a new optimal transport distance, called the Fused Gromov-Wasserstein distance, capable of leveraging both structural and feature information by combining both views and prove its metric properties over very general manifolds. We also define the barycenter of structured objects as their Fr\'echet mean, leveraging both feature and structural information. We illustrate the versatility of the method for problems where structured objects are involved, computing barycenters in graph and time series contexts. We also use this new distance for graph classification where we obtain comparable or superior results than state-of-the-art graph kernel methods and end-to-end graph CNN approach.

Wasserstein Discriminant Analysis

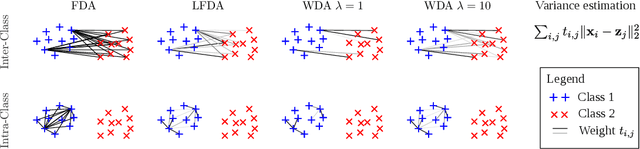
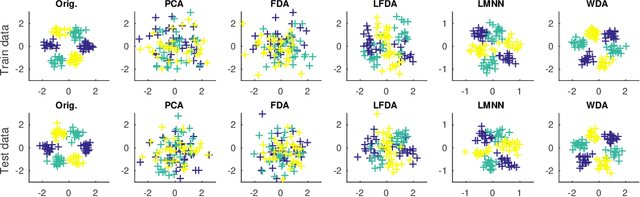
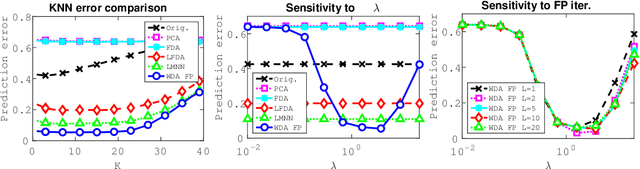
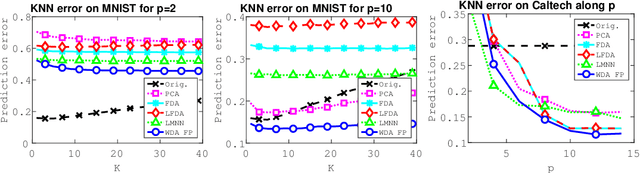
Wasserstein Discriminant Analysis (WDA) is a new supervised method that can improve classification of high-dimensional data by computing a suitable linear map onto a lower dimensional subspace. Following the blueprint of classical Linear Discriminant Analysis (LDA), WDA selects the projection matrix that maximizes the ratio of two quantities: the dispersion of projected points coming from different classes, divided by the dispersion of projected points coming from the same class. To quantify dispersion, WDA uses regularized Wasserstein distances, rather than cross-variance measures which have been usually considered, notably in LDA. Thanks to the the underlying principles of optimal transport, WDA is able to capture both global (at distribution scale) and local (at samples scale) interactions between classes. Regularized Wasserstein distances can be computed using the Sinkhorn matrix scaling algorithm; We show that the optimization of WDA can be tackled using automatic differentiation of Sinkhorn iterations. Numerical experiments show promising results both in terms of prediction and visualization on toy examples and real life datasets such as MNIST and on deep features obtained from a subset of the Caltech dataset.

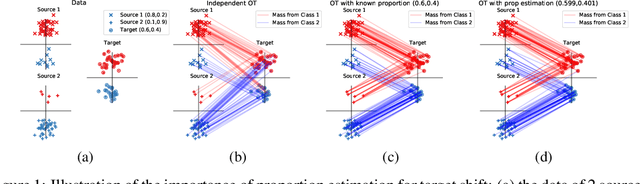
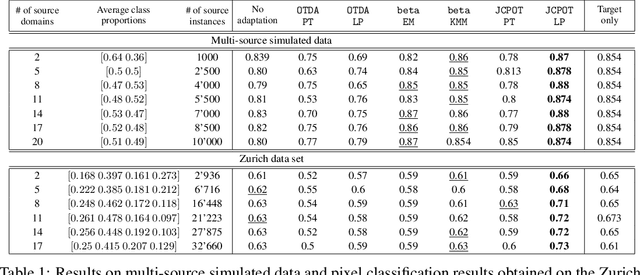
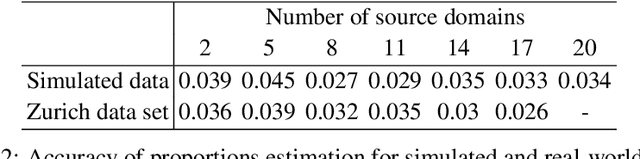
Optimal Transport for Multi-source Domain Adaptation under Target Shift

In this paper, we propose to tackle the problem of reducing discrepancies between multiple domains referred to as multi-source domain adaptation and consider it under the target shift assumption: in all domains we aim to solve a classification problem with the same output classes, but with labels' proportions differing across them. This problem, generally ignored in the vast majority papers on domain adaptation papers, is nevertheless critical in real-world applications, and we theoretically show its impact on the adaptation success. To address this issue, we design a method based on optimal transport, a theory that has been successfully used to tackle adaptation problems in machine learning. Our method performs multi-source adaptation and target shift correction simultaneously by learning the class probabilities of the unlabeled target sample and the coupling allowing to align two (or more) probability distributions. Experiments on both synthetic and real-world data related to satellite image segmentation task show the superiority of the proposed method over the state-of-the-art.

Wasserstein Distance Measure Machines

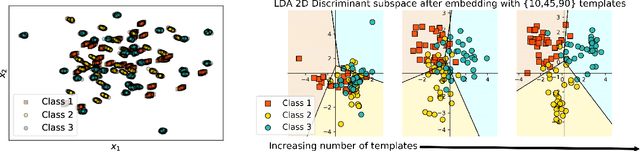
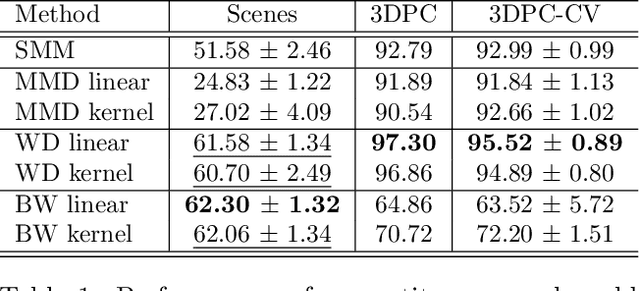
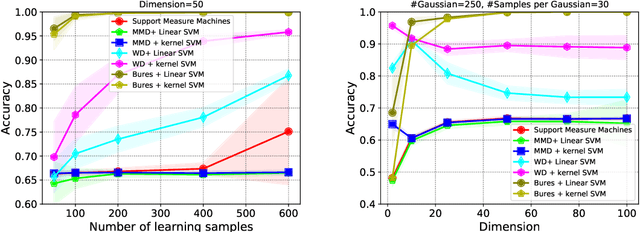
This paper presents a distance-based discriminative framework for learning with probability distributions. Instead of using kernel mean embeddings or generalized radial basis kernels, we introduce embeddings based on dissimilarity of distributions to some reference distributions denoted as templates. Our framework extends the theory of similarity of \citet{balcan2008theory} to the population distribution case and we prove that, for some learning problems, Wasserstein distance achieves low-error linear decision functions with high probability. Our key result is to prove that the theory also holds for empirical distributions. Algorithmically, the proposed approach is very simple as it consists in computing a mapping based on pairwise Wasserstein distances and then learning a linear decision function. Our experimental results show that this Wasserstein distance embedding performs better than kernel mean embeddings and computing Wasserstein distance is far more tractable than estimating pairwise Kullback-Leibler divergence of empirical distributions.

Large-Scale Optimal Transport and Mapping Estimation

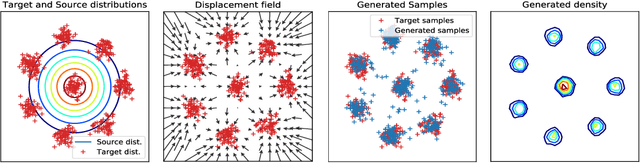
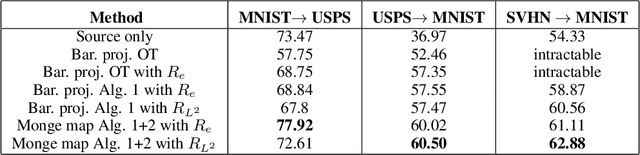
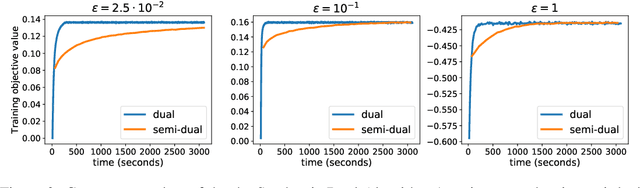
This paper presents a novel two-step approach for the fundamental problem of learning an optimal map from one distribution to another. First, we learn an optimal transport (OT) plan, which can be thought as a one-to-many map between the two distributions. To that end, we propose a stochastic dual approach of regularized OT, and show empirically that it scales better than a recent related approach when the amount of samples is very large. Second, we estimate a \textit{Monge map} as a deep neural network learned by approximating the barycentric projection of the previously-obtained OT plan. This parameterization allows generalization of the mapping outside the support of the input measure. We prove two theoretical stability results of regularized OT which show that our estimations converge to the OT plan and Monge map between the underlying continuous measures. We showcase our proposed approach on two applications: domain adaptation and generative modeling.

Data Dependent Kernel Approximation using Pseudo Random Fourier Features

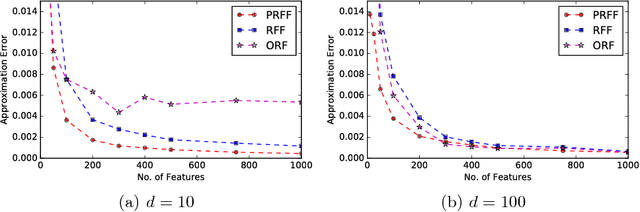
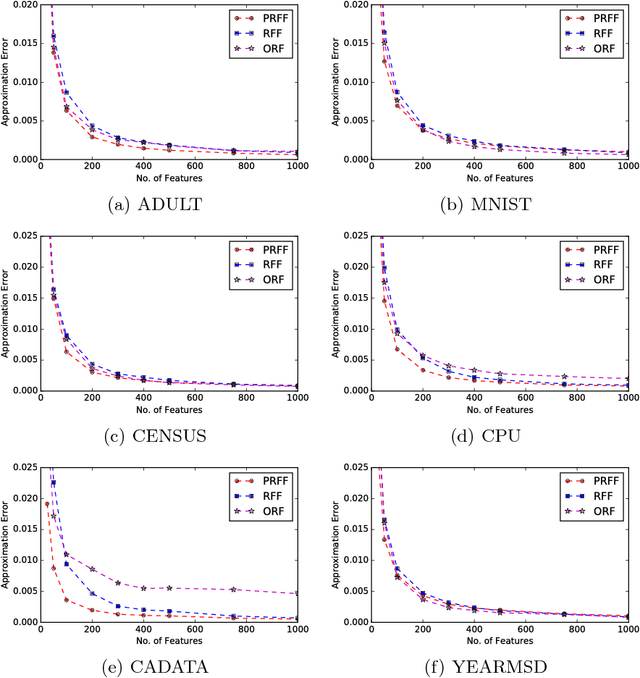
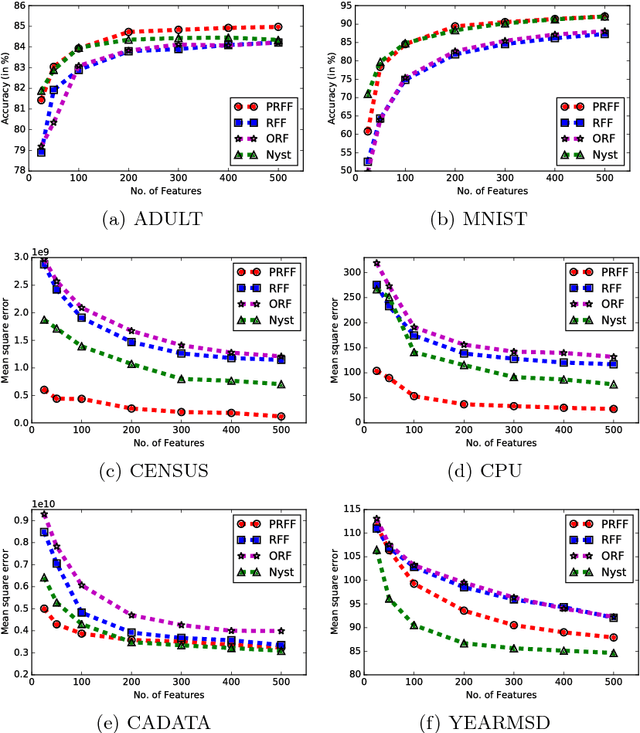
Kernel methods are powerful and flexible approach to solve many problems in machine learning. Due to the pairwise evaluations in kernel methods, the complexity of kernel computation grows as the data size increases; thus the applicability of kernel methods is limited for large scale datasets. Random Fourier Features (RFF) has been proposed to scale the kernel method for solving large scale datasets by approximating kernel function using randomized Fourier features. While this method proved very popular, still it exists shortcomings to be effectively used. As RFF samples the randomized features from a distribution independent of training data, it requires sufficient large number of feature expansions to have similar performances to kernelized classifiers, and this is proportional to the number samples in the dataset. Thus, reducing the number of feature dimensions is necessary to effectively scale to large datasets. In this paper, we propose a kernel approximation method in a data dependent way, coined as Pseudo Random Fourier Features (PRFF) for reducing the number of feature dimensions and also to improve the prediction performance. The proposed approach is evaluated on classification and regression problems and compared with the RFF, orthogonal random features and Nystr{\"o}m approach

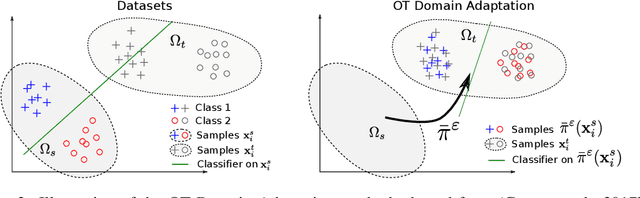
Joint Distribution Optimal Transportation for Domain Adaptation

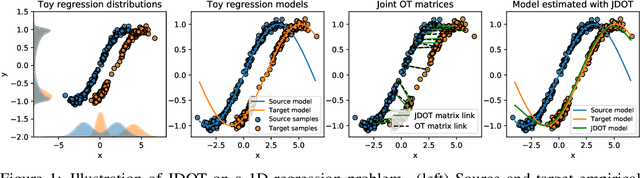
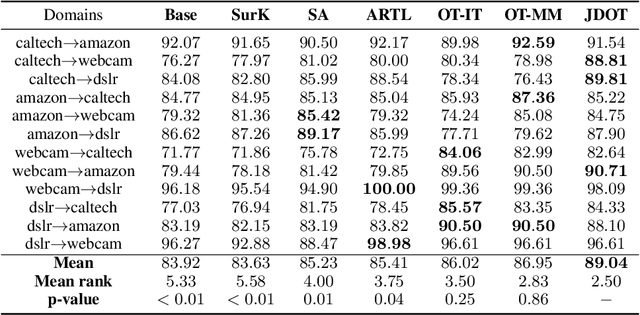
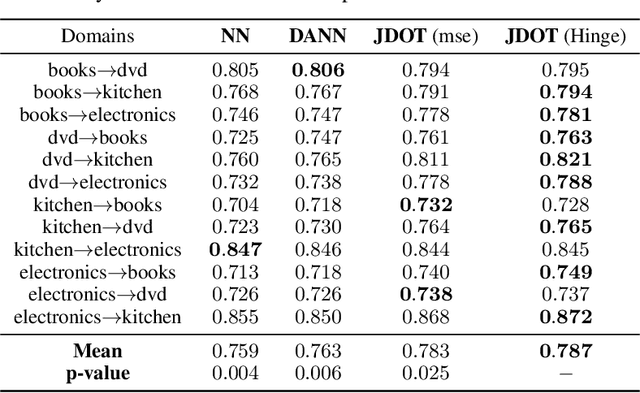
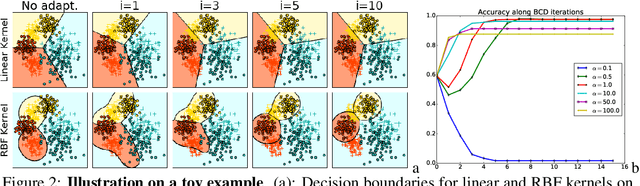
This paper deals with the unsupervised domain adaptation problem, where one wants to estimate a prediction function $f$ in a given target domain without any labeled sample by exploiting the knowledge available from a source domain where labels are known. Our work makes the following assumption: there exists a non-linear transformation between the joint feature/label space distributions of the two domain $\mathcal{P}_s$ and $\mathcal{P}_t$. We propose a solution of this problem with optimal transport, that allows to recover an estimated target $\mathcal{P}^f_t=(X,f(X))$ by optimizing simultaneously the optimal coupling and $f$. We show that our method corresponds to the minimization of a bound on the target error, and provide an efficient algorithmic solution, for which convergence is proved. The versatility of our approach, both in terms of class of hypothesis or loss functions is demonstrated with real world classification and regression problems, for which we reach or surpass state-of-the-art results.