Hierarchical Feature-level Reverse Propagation for Post-Training Neural Networks

End-to-end autonomous driving has emerged as a dominant paradigm, yet its highly entangled black-box models pose significant challenges in terms of interpretability and safety assurance. To improve model transparency and training flexibility, this paper proposes a hierarchical and decoupled post-training framework tailored for pretrained neural networks. By reconstructing intermediate feature maps from ground-truth labels, surrogate supervisory signals are introduced at transitional layers to enable independent training of specific components, thereby avoiding the complexity and coupling of conventional end-to-end backpropagation and providing interpretable insights into networks' internal mechanisms. To the best of our knowledge, this is the first method to formalize feature-level reverse computation as well-posed optimization problems, which we rigorously reformulate as systems of linear equations or least squares problems. This establishes a novel and efficient training paradigm that extends gradient backpropagation to feature backpropagation. Extensive experiments on multiple standard image classification benchmarks demonstrate that the proposed method achieves superior generalization performance and computational efficiency compared to traditional training approaches, validating its effectiveness and potential.

$α$-GAN by Rényi Cross Entropy

This paper proposes $\alpha$-GAN, a generative adversarial network using R\'{e}nyi measures. The value function is formulated, by R\'{e}nyi cross entropy, as an expected certainty measure incurred by the discriminator's soft decision as to where the sample is from, true population or the generator. The discriminator tries to maximize the R\'{e}nyi certainty about sample source, while the generator wants to reduce it by injecting fake samples. This forms a min-max problem with the solution parameterized by the R\'{e}nyi order $\alpha$. This $\alpha$-GAN reduces to vanilla GAN at $\alpha = 1$, where the value function is exactly the binary cross entropy. The optimization of $\alpha$-GAN is over probability (vector) space. It is shown that the gradient is exponentially enlarged when R\'{e}nyi order is in the range $\alpha \in (0,1)$. This makes convergence faster, which is verified by experimental results. A discussion shows that choosing $\alpha \in (0,1)$ may be able to solve some common problems, e.g., vanishing gradient. A following observation reveals that this range has not been fully explored in the existing R\'{e}nyi version GANs.

On Monotonicity of the Optimal Transmission Policy in Cross-layer Adaptive m-QAM Modulation

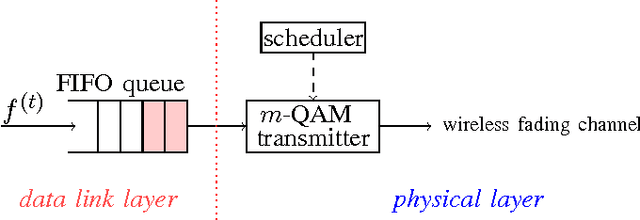
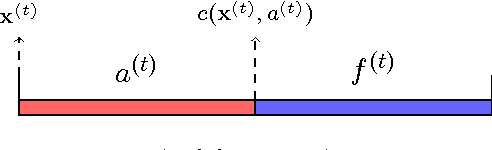
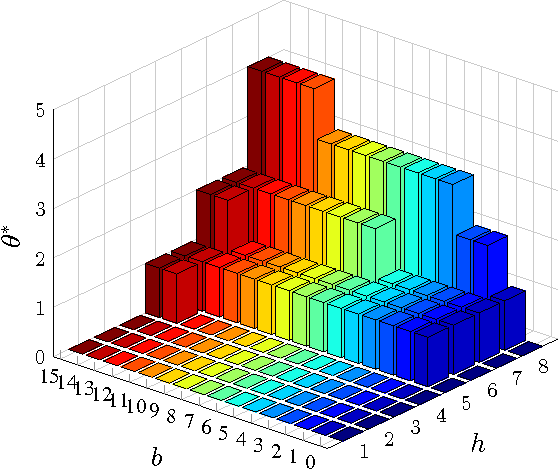
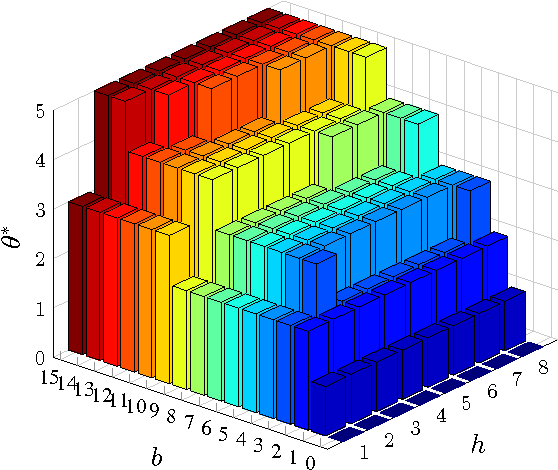
This paper considers a cross-layer adaptive modulation system that is modeled as a Markov decision process (MDP). We study how to utilize the monotonicity of the optimal transmission policy to relieve the computational complexity of dynamic programming (DP). In this system, a scheduler controls the bit rate of the m-quadrature amplitude modulation (m-QAM) in order to minimize the long-term losses incurred by the queue overflow in the data link layer and the transmission power consumption in the physical layer. The work is done in two steps. Firstly, we observe the L-natural-convexity and submodularity of DP to prove that the optimal policy is always nondecreasing in queue occupancy/state and derive the sufficient condition for it to be nondecreasing in both queue and channel states. We also show that, due to the L-natural-convexity of DP, the variation of the optimal policy in queue state is restricted by a bounded marginal effect: The increment of the optimal policy between adjacent queue states is no greater than one. Secondly, we use the monotonicity results to present two low complexity algorithms: monotonic policy iteration (MPI) based on L-natural-convexity and discrete simultaneous perturbation stochastic approximation (DSPSA). We run experiments to show that the time complexity of MPI based on L-natural-convexity is much lower than that of DP and the conventional MPI that is based on submodularity and DSPSA is able to adaptively track the optimal policy when the system parameters change.

Structured Optimal Transmission Control in Network-coded Two-way Relay Channels

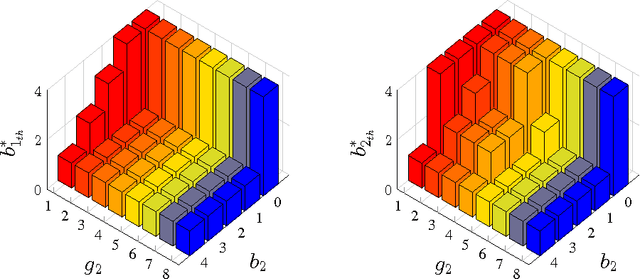
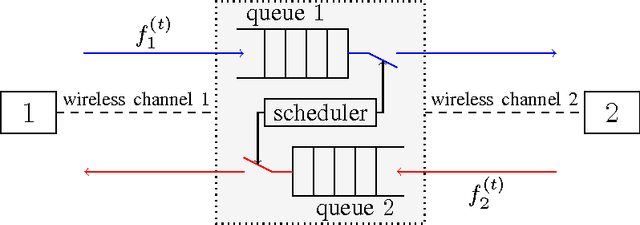
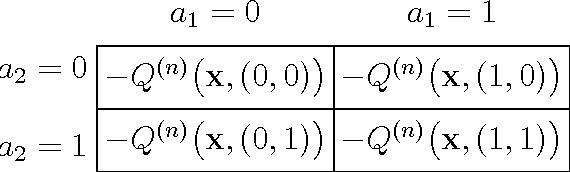
This paper considers a transmission control problem in network-coded two-way relay channels (NC-TWRC), where the relay buffers random symbol arrivals from two users, and the channels are assumed to be fading. The problem is modeled by a discounted infinite horizon Markov decision process (MDP). The objective is to find a transmission control policy that minimizes the symbol delay, buffer overflow and transmission power consumption and error rate simultaneously and in the long run. By using the concepts of submodularity, multimodularity and L-natural convexity, we study the structure of the optimal policy searched by dynamic programming (DP) algorithm. We show that the optimal transmission policy is nondecreasing in queue occupancies or/and channel states under certain conditions such as the chosen values of parameters in the MDP model, channel modeling method, modulation scheme and the preservation of stochastic dominance in the transitions of system states. The results derived in this paper can be used to relieve the high complexity of DP and facilitate real-time control.