ARC-Flow : Articulated, Resolution-Agnostic, Correspondence-Free Matching and Interpolation of 3D Shapes Under Flow Fields

This work presents a unified framework for the unsupervised prediction of physically plausible interpolations between two 3D articulated shapes and the automatic estimation of dense correspondence between them. Interpolation is modelled as a diffeomorphic transformation using a smooth, time-varying flow field governed by Neural Ordinary Differential Equations (ODEs). This ensures topological consistency and non-intersecting trajectories while accommodating hard constraints, such as volume preservation, and soft constraints, \eg physical priors. Correspondence is recovered using an efficient Varifold formulation, that is effective on high-fidelity surfaces with differing parameterisations. By providing a simple skeleton for the source shape only, we impose physically motivated constraints on the deformation field and resolve symmetric ambiguities. This is achieved without relying on skinning weights or any prior knowledge of the skeleton's target pose configuration. Qualitative and quantitative results demonstrate competitive or superior performance over existing state-of-the-art approaches in both shape correspondence and interpolation tasks across standard datasets.

Likelihood-based Out-of-Distribution Detection with Denoising Diffusion Probabilistic Models

Out-of-Distribution detection between dataset pairs has been extensively explored with generative models. We show that likelihood-based Out-of-Distribution detection can be extended to diffusion models by leveraging the fact that they, like other likelihood-based generative models, are dramatically affected by the input sample complexity. Currently, all Out-of-Distribution detection methods with Diffusion Models are reconstruction-based. We propose a new likelihood ratio for Out-of-Distribution detection with Deep Denoising Diffusion Models, which we call the Complexity Corrected Likelihood Ratio. Our likelihood ratio is constructed using Evidence Lower-Bound evaluations from an individual model at various noising levels. We present results that are comparable to state-of-the-art Out-of-Distribution detection methods with generative models.

The Robust Semantic Segmentation UNCV2023 Challenge Results

This paper outlines the winning solutions employed in addressing the MUAD uncertainty quantification challenge held at ICCV 2023. The challenge was centered around semantic segmentation in urban environments, with a particular focus on natural adversarial scenarios. The report presents the results of 19 submitted entries, with numerous techniques drawing inspiration from cutting-edge uncertainty quantification methodologies presented at prominent conferences in the fields of computer vision and machine learning and journals over the past few years. Within this document, the challenge is introduced, shedding light on its purpose and objectives, which primarily revolved around enhancing the robustness of semantic segmentation in urban scenes under varying natural adversarial conditions. The report then delves into the top-performing solutions. Moreover, the document aims to provide a comprehensive overview of the diverse solutions deployed by all participants. By doing so, it seeks to offer readers a deeper insight into the array of strategies that can be leveraged to effectively handle the inherent uncertainties associated with autonomous driving and semantic segmentation, especially within urban environments.

Compressed Sensing MRI Reconstruction Regularized by VAEs with Structured Image Covariance

Learned regularization for MRI reconstruction can provide complex data-driven priors to inverse problems while still retaining the control and insight of a variational regularization method. Moreover, unsupervised learning, without paired training data, allows the learned regularizer to remain flexible to changes in the forward problem such as noise level, sampling pattern or coil sensitivities. One such approach uses generative models, trained on ground-truth images, as priors for inverse problems, penalizing reconstructions far from images the generator can produce. In this work, we utilize variational autoencoders (VAEs) that generate not only an image but also a covariance uncertainty matrix for each image. The covariance can model changing uncertainty dependencies caused by structure in the image, such as edges or objects, and provides a new distance metric from the manifold of learned images. We demonstrate these novel generative regularizers on radially sub-sampled MRI knee measurements from the fastMRI dataset and compare them to other unlearned, unsupervised and supervised methods. Our results show that the proposed method is competitive with other state-of-the-art methods and behaves consistently with changing sampling patterns and noise levels.

Learning Structured Gaussians to Approximate Deep Ensembles

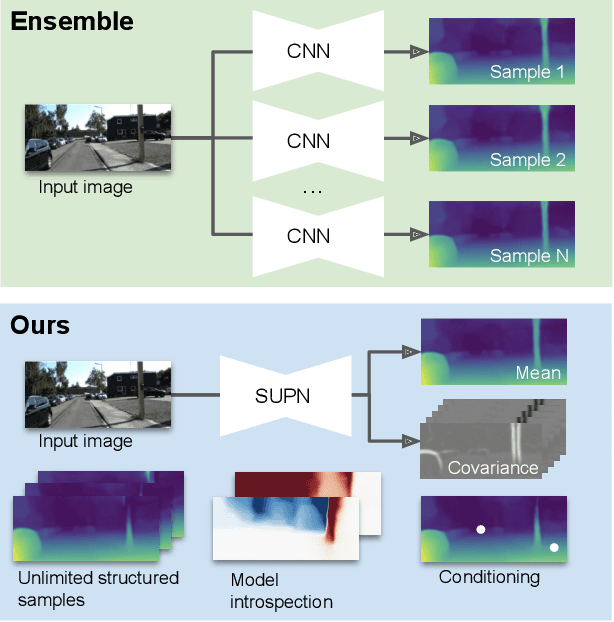
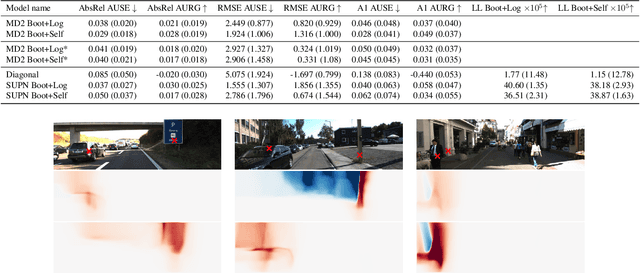
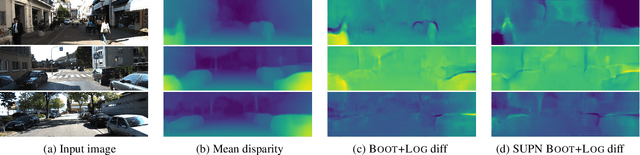
This paper proposes using a sparse-structured multivariate Gaussian to provide a closed-form approximator for the output of probabilistic ensemble models used for dense image prediction tasks. This is achieved through a convolutional neural network that predicts the mean and covariance of the distribution, where the inverse covariance is parameterised by a sparsely structured Cholesky matrix. Similarly to distillation approaches, our single network is trained to maximise the probability of samples from pre-trained probabilistic models, in this work we use a fixed ensemble of networks. Once trained, our compact representation can be used to efficiently draw spatially correlated samples from the approximated output distribution. Importantly, this approach captures the uncertainty and structured correlations in the predictions explicitly in a formal distribution, rather than implicitly through sampling alone. This allows direct introspection of the model, enabling visualisation of the learned structure. Moreover, this formulation provides two further benefits: estimation of a sample probability, and the introduction of arbitrary spatial conditioning at test time. We demonstrate the merits of our approach on monocular depth estimation and show that the advantages of our approach are obtained with comparable quantitative performance.

Understanding Training-Data Leakage from Gradients in Neural Networks for Image Classification

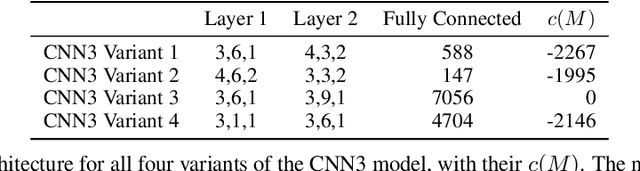
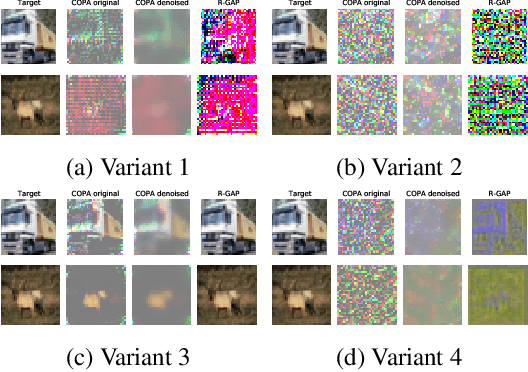
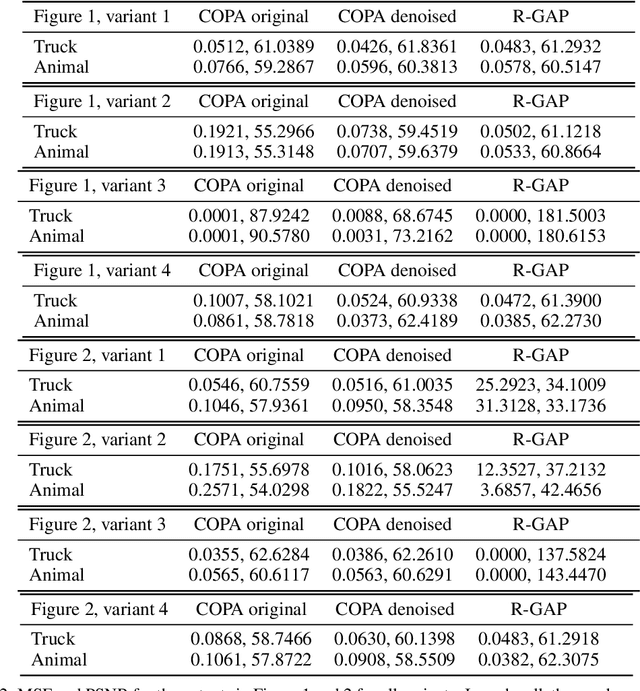
Federated learning of deep learning models for supervised tasks, e.g. image classification and segmentation, has found many applications: for example in human-in-the-loop tasks such as film post-production where it enables sharing of domain expertise of human artists in an efficient and effective fashion. In many such applications, we need to protect the training data from being leaked when gradients are shared in the training process due to IP or privacy concerns. Recent works have demonstrated that it is possible to reconstruct the training data from gradients for an image-classification model when its architecture is known. However, there is still an incomplete theoretical understanding of the efficacy and failure of such attacks. In this paper, we analyse the source of training-data leakage from gradients. We formulate the problem of training data reconstruction as solving an optimisation problem iteratively for each layer. The layer-wise objective function is primarily defined by weights and gradients from the current layer as well as the output from the reconstruction of the subsequent layer, but it might also involve a 'pull-back' constraint from the preceding layer. Training data can be reconstructed when we solve the problem backward from the output of the network through each layer. Based on this formulation, we are able to attribute the potential leakage of the training data in a deep network to its architecture. We also propose a metric to measure the level of security of a deep learning model against gradient-based attacks on the training data.

Aligned Multi-Task Gaussian Process

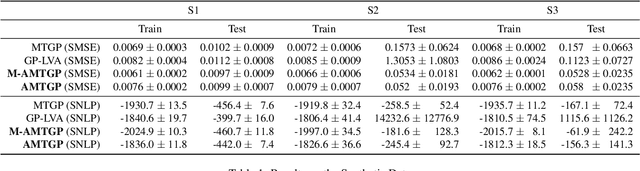
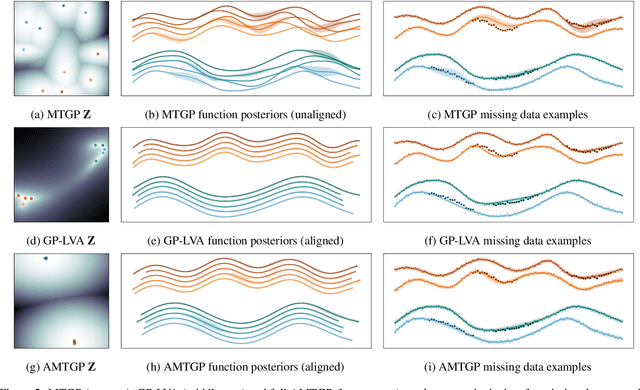
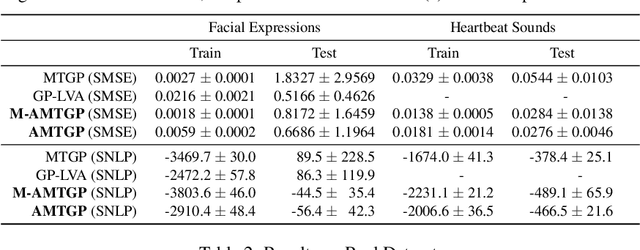
Multi-task learning requires accurate identification of the correlations between tasks. In real-world time-series, tasks are rarely perfectly temporally aligned; traditional multi-task models do not account for this and subsequent errors in correlation estimation will result in poor predictive performance and uncertainty quantification. We introduce a method that automatically accounts for temporal misalignment in a unified generative model that improves predictive performance. Our method uses Gaussian processes (GPs) to model the correlations both within and between the tasks. Building on the previous work by Kazlauskaiteet al. [2019], we include a separate monotonic warp of the input data to model temporal misalignment. In contrast to previous work, we formulate a lower bound that accounts for uncertainty in both the estimates of the warping process and the underlying functions. Also, our new take on a monotonic stochastic process, with efficient path-wise sampling for the warp functions, allows us to perform full Bayesian inference in the model rather than MAP estimates. Missing data experiments, on synthetic and real time-series, demonstrate the advantages of accounting for misalignments (vs standard unaligned method) as well as modelling the uncertainty in the warping process(vs baseline MAP alignment approach).

Regularising Inverse Problems with Generative Machine Learning Models

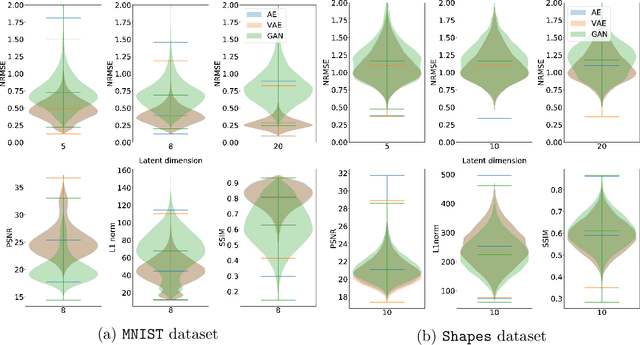
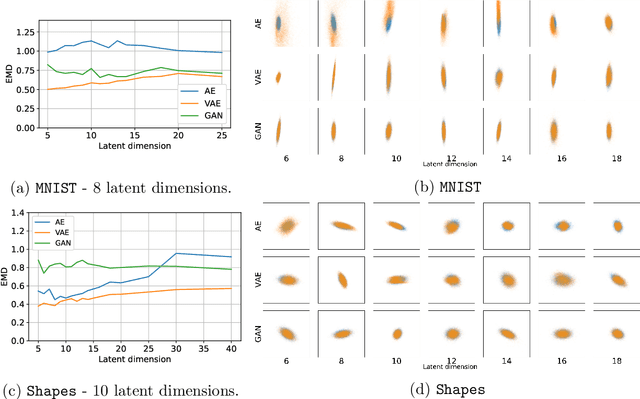
Deep neural network approaches to inverse imaging problems have produced impressive results in the last few years. In this paper, we consider the use of generative models in a variational regularisation approach to inverse problems. The considered regularisers penalise images that are far from the range of a generative model that has learned to produce images similar to a training dataset. We name this family \textit{generative regularisers}. The success of generative regularisers depends on the quality of the generative model and so we propose a set of desired criteria to assess models and guide future research. In our numerical experiments, we evaluate three common generative models, autoencoders, variational autoencoders and generative adversarial networks, against our desired criteria. We also test three different generative regularisers on the inverse problems of deblurring, deconvolution, and tomography. We show that the success of solutions restricted to lie exactly in the range of the generator is highly dependent on the ability of the generative model but that allowing small deviations from the range of the generator produces more consistent results.

Black-box density function estimation using recursive partitioning

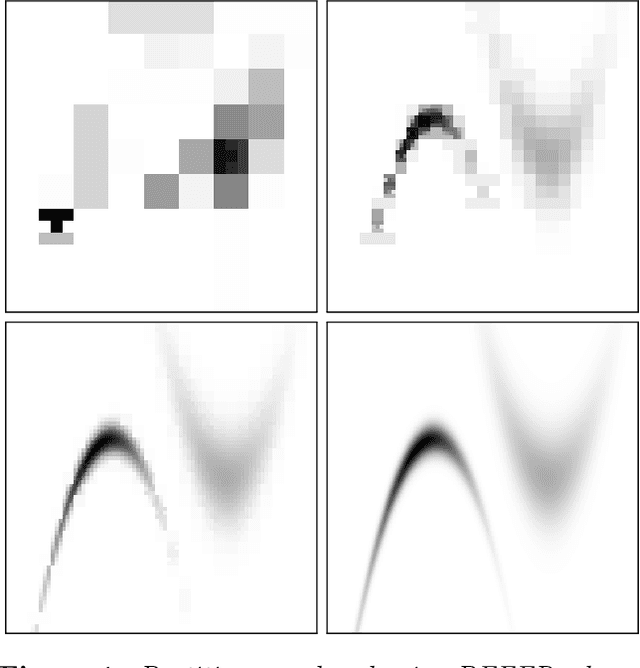
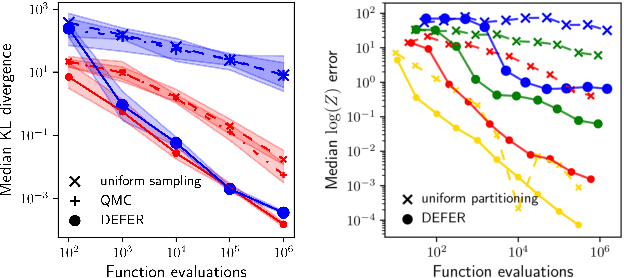
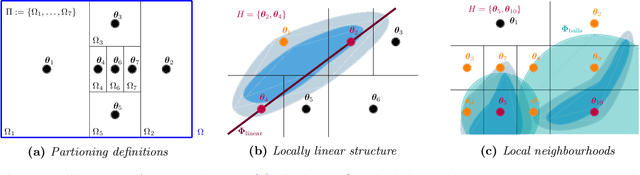
We present a novel approach to Bayesian inference and general Bayesian computation that is defined through a recursive partitioning of the sample space. It does not rely on gradients, nor require any problem-specific tuning, and is asymptotically exact for any density function with a bounded domain. The output is an approximation to the whole density function including the normalization constant, via partitions organized in efficient data structures. This allows for evidence estimation, as well as approximate posteriors that allow for fast sampling and fast evaluations of the density. It shows competitive performance to recent state-of-the-art methods on synthetic and real-world problem examples including parameter inference for gravitational-wave physics.

DiverseNet: When One Right Answer is not Enough

Many structured prediction tasks in machine vision have a collection of acceptable answers, instead of one definitive ground truth answer. Segmentation of images, for example, is subject to human labeling bias. Similarly, there are multiple possible pixel values that could plausibly complete occluded image regions. State-of-the art supervised learning methods are typically optimized to make a single test-time prediction for each query, failing to find other modes in the output space. Existing methods that allow for sampling often sacrifice speed or accuracy. We introduce a simple method for training a neural network, which enables diverse structured predictions to be made for each test-time query. For a single input, we learn to predict a range of possible answers. We compare favorably to methods that seek diversity through an ensemble of networks. Such stochastic multiple choice learning faces mode collapse, where one or more ensemble members fail to receive any training signal. Our best performing solution can be deployed for various tasks, and just involves small modifications to the existing single-mode architecture, loss function, and training regime. We demonstrate that our method results in quantitative improvements across three challenging tasks: 2D image completion, 3D volume estimation, and flow prediction.