SMC Is All You Need: Parallel Strong Scaling

In the general framework of Bayesian inference, the target distribution can only be evaluated up-to a constant of proportionality. Classical consistent Bayesian methods such as sequential Monte Carlo (SMC) and Markov chain Monte Carlo (MCMC) have unbounded time complexity requirements. We develop a fully parallel sequential Monte Carlo (pSMC) method which provably delivers parallel strong scaling, i.e. the time complexity (and per-node memory) remains bounded if the number of asynchronous processes is allowed to grow. More precisely, the pSMC has a theoretical convergence rate of MSE$ = O(1/NR)$, where $N$ denotes the number of communicating samples in each processor and $R$ denotes the number of processors. In particular, for suitably-large problem-dependent $N$, as $R \rightarrow \infty$ the method converges to infinitesimal accuracy MSE$=O(\varepsilon^2)$ with a fixed finite time-complexity Cost$=O(1)$ and with no efficiency leakage, i.e. computational complexity Cost$=O(\varepsilon^{-2})$. A number of Bayesian inference problems are taken into consideration to compare the pSMC and MCMC methods.

Accelerating Look-ahead in Bayesian Optimization: Multilevel Monte Carlo is All you Need

We leverage multilevel Monte Carlo (MLMC) to improve the performance of multi-step look-ahead Bayesian optimization (BO) methods that involve nested expectations and maximizations. The complexity rate of naive Monte Carlo degrades for nested operations, whereas MLMC is capable of achieving the canonical Monte Carlo convergence rate for this type of problem, independently of dimension and without any smoothness assumptions. Our theoretical study focuses on the approximation improvements for one- and two-step look-ahead acquisition functions, but, as we discuss, the approach is generalizable in various ways, including beyond the context of BO. Findings are verified numerically and the benefits of MLMC for BO are illustrated on several benchmark examples. Code is available here https://github.com/Shangda-Yang/MLMCBO.

Multilevel Bayesian Deep Neural Networks

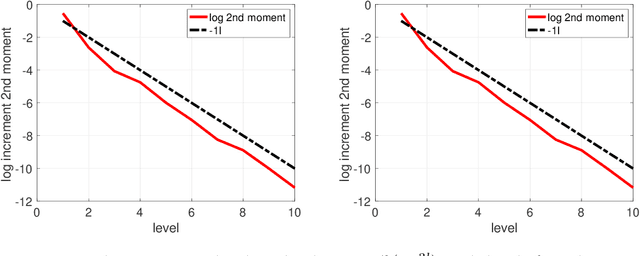
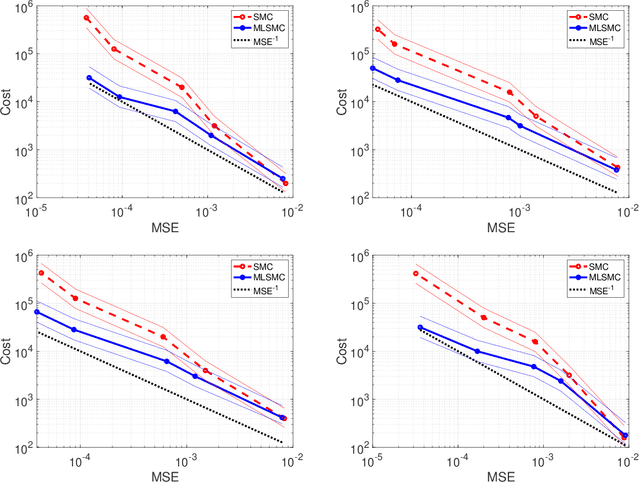
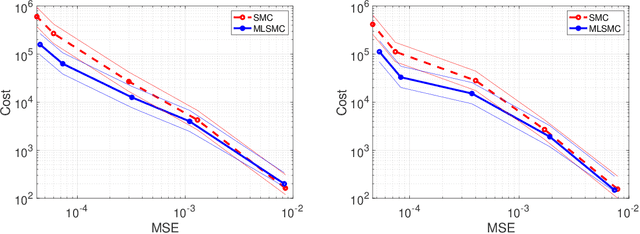
In this article we consider Bayesian inference associated to deep neural networks (DNNs) and in particular, trace-class neural network (TNN) priors which were proposed by Sell et al. [39]. Such priors were developed as more robust alternatives to classical architectures in the context of inference problems. For this work we develop multilevel Monte Carlo (MLMC) methods for such models. MLMC is a popular variance reduction technique, with particular applications in Bayesian statistics and uncertainty quantification. We show how a particular advanced MLMC method that was introduced in [4] can be applied to Bayesian inference from DNNs and establish mathematically, that the computational cost to achieve a particular mean square error, associated to posterior expectation computation, can be reduced by several orders, versus more conventional techniques. To verify such results we provide numerous numerical experiments on model problems arising in machine learning. These include Bayesian regression, as well as Bayesian classification and reinforcement learning.

Digital Fingerprinting of Microstructures

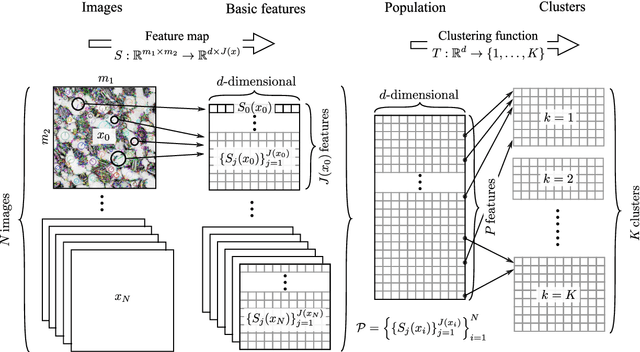
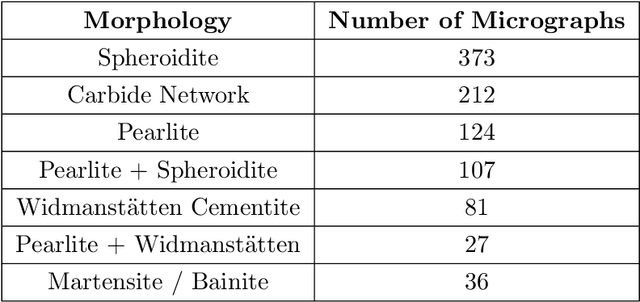
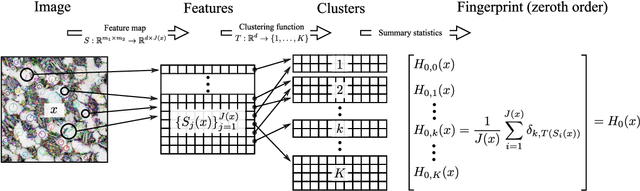
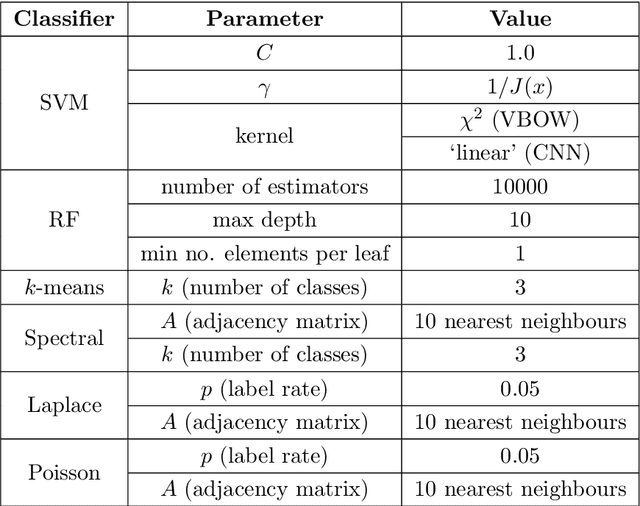
Finding efficient means of fingerprinting microstructural information is a critical step towards harnessing data-centric machine learning approaches. A statistical framework is systematically developed for compressed characterisation of a population of images, which includes some classical computer vision methods as special cases. The focus is on materials microstructure. The ultimate purpose is to rapidly fingerprint sample images in the context of various high-throughput design/make/test scenarios. This includes, but is not limited to, quantification of the disparity between microstructures for quality control, classifying microstructures, predicting materials properties from image data and identifying potential processing routes to engineer new materials with specific properties. Here, we consider microstructure classification and utilise the resulting features over a range of related machine learning tasks, namely supervised, semi-supervised, and unsupervised learning. The approach is applied to two distinct datasets to illustrate various aspects and some recommendations are made based on the findings. In particular, methods that leverage transfer learning with convolutional neural networks (CNNs), pretrained on the ImageNet dataset, are generally shown to outperform other methods. Additionally, dimensionality reduction of these CNN-based fingerprints is shown to have negligible impact on classification accuracy for the supervised learning approaches considered. In situations where there is a large dataset with only a handful of images labelled, graph-based label propagation to unlabelled data is shown to be favourable over discarding unlabelled data and performing supervised learning. In particular, label propagation by Poisson learning is shown to be highly effective at low label rates.

Sparse online variational Bayesian regression

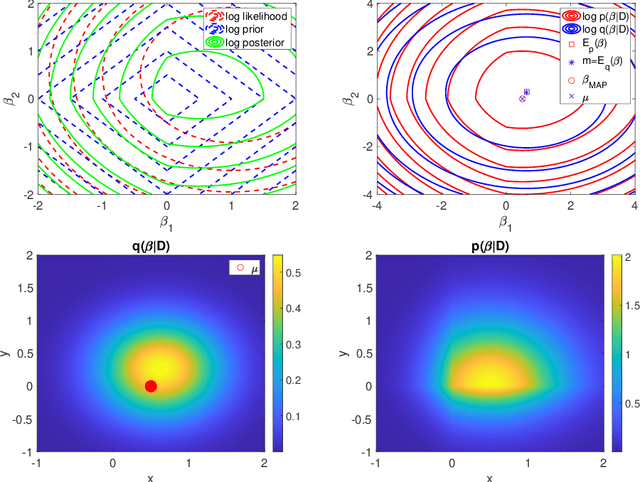
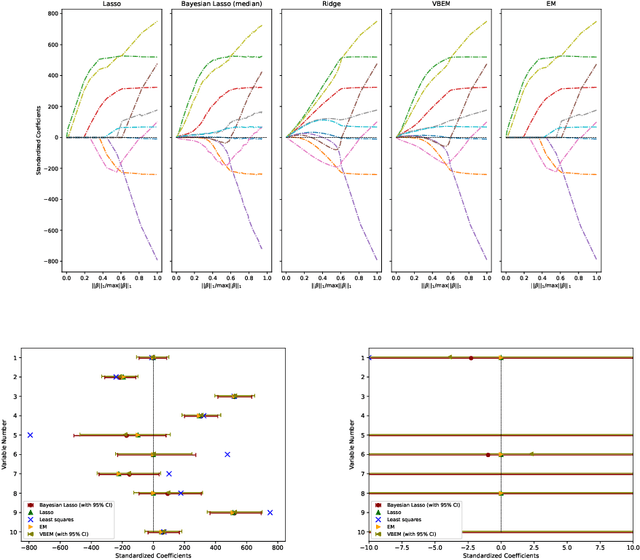
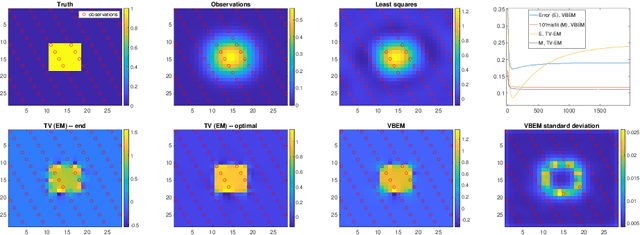
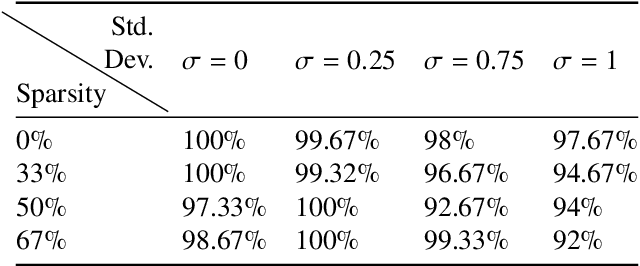
This work considers variational Bayesian inference as an inexpensive and scalable alternative to a fully Bayesian approach in the context of sparsity-promoting priors. In particular, the priors considered arise from scale mixtures of Normal distributions with a generalized inverse Gaussian mixing distribution. This includes the variational Bayesian LASSO as an inexpensive and scalable alternative to the Bayesian LASSO introduced in [56]. It also includes priors which more strongly promote sparsity. For linear models the method requires only the iterative solution of deterministic least squares problems. Furthermore, for $n\rightarrow \infty$ data points and p unknown covariates the method can be implemented exactly online with a cost of O(p$^3$) in computation and O(p$^2$) in memory. For large p an approximation is able to achieve promising results for a cost of O(p) in both computation and memory. Strategies for hyper-parameter tuning are also considered. The method is implemented for real and simulated data. It is shown that the performance in terms of variable selection and uncertainty quantification of the variational Bayesian LASSO can be comparable to the Bayesian LASSO for problems which are tractable with that method, and for a fraction of the cost. The present method comfortably handles n = p = 131,073 on a laptop in minutes, and n = 10$^5$, p = 10$^6$ overnight.

Materials Fingerprinting Classification

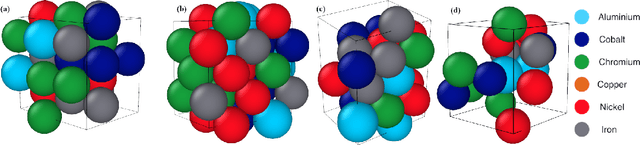
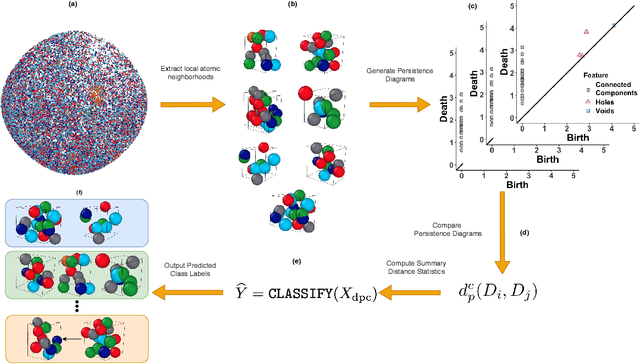
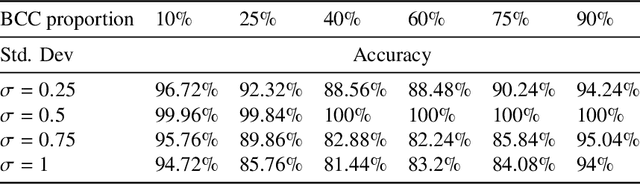
Significant progress in many classes of materials could be made with the availability of experimentally-derived large datasets composed of atomic identities and three-dimensional coordinates. Methods for visualizing the local atomic structure, such as atom probe tomography (APT), which routinely generate datasets comprised of millions of atoms, are an important step in realizing this goal. However, state-of-the-art APT instruments generate noisy and sparse datasets that provide information about elemental type, but obscure atomic structures, thus limiting their subsequent value for materials discovery. The application of a materials fingerprinting process, a machine learning algorithm coupled with topological data analysis, provides an avenue by which here-to-fore unprecedented structural information can be extracted from an APT dataset. As a proof of concept, the material fingerprint is applied to high-entropy alloy APT datasets containing body-centered cubic (BCC) and face-centered cubic (FCC) crystal structures. A local atomic configuration centered on an arbitrary atom is assigned a topological descriptor, with which it can be characterized as a BCC or FCC lattice with near perfect accuracy, despite the inherent noise in the dataset. This successful identification of a fingerprint is a crucial first step in the development of algorithms which can extract more nuanced information, such as chemical ordering, from existing datasets of complex materials.

Cluster, Classify, Regress: A General Method For Learning Discountinous Functions

This paper presents a method for solving the supervised learning problem in which the output is highly nonlinear and discontinuous. It is proposed to solve this problem in three stages: (i) cluster the pairs of input-output data points, resulting in a label for each point; (ii) classify the data, where the corresponding label is the output; and finally (iii) perform one separate regression for each class, where the training data corresponds to the subset of the original input-output pairs which have that label according to the classifier. It has not yet been proposed to combine these 3 fundamental building blocks of machine learning in this simple and powerful fashion. This can be viewed as a form of deep learning, where any of the intermediate layers can itself be deep. The utility and robustness of the methodology is illustrated on some toy problems, including one example problem arising from simulation of plasma fusion in a tokamak.