Improving the decoding performance of CA-polar codes

We investigate the use of modern code-agnostic decoders to convert CA-SCL from an incomplete decoder to a complete one. When CA-SCL fails to identify a codeword that passes the CRC check, we apply a code-agnostic decoder that identifies a codeword that satisfies the CRC. We establish that this approach gives gains of up to 0.2 dB in block error rate for CA-Polar codes from the 5G New Radio standard. If, instead, the message had been encoded in a systematic CA-polar code, the gain improves to 0.2 ~ 1dB. Leveraging recent developments in blockwise soft output, we additionally establish that it is possible to control the undetected error rate even when using the CRC for error correction.

Enhanced GCD through ORBGRAND-AI: Exploiting Partial and Total Correlation in Noise

There have been significant advances in recent years in the development of forward error correction decoders that can decode codes of any structure, including practical realizations in synthesized circuits and taped out chips. While essentially all soft-decision decoders assume that bits have been impacted independently on the channel, for one of these new approaches it has been established that channel dependencies can be exploited to achieve superior decoding accuracy, resulting in Ordered Reliability Bits Guessing Random Additive Noise Decoding Approximate Independence (ORBGRAND-AI). Building on that capability, here we consider the integration of ORBGRAND-AI as a pattern generator for Guessing Codeword Decoding (GCD). We first establish that a direct approach delivers mildly degraded block error rate (BLER) but with reduced number of queried patterns when compared to ORBGRAND-AI. We then show that with a more nuanced approach it is possible to leverage total correlation to deliver an additional BLER improvement of around 0.75 dB while retaining reduced query numbers.

Joint Error Correction and Fading Channel Estimation Enhancement Leveraging GRAND

We present a novel method for error correction in the presence of fading channel estimation errors (CEE). When such errors are significant, considerable performance losses can be observed if the wireless transceiver is not adapted. Instead of refining the estimate by increasing the pilot sequence length or improving the estimation algorithm, we propose two new approaches based on Guessing Random Additive Noise Decoding (GRAND) decoders. The first method involves testing multiple candidates for the channel estimate located in the complex neighborhood around the original pilot-based estimate. All these candidates are employed in parallel to compute log-likelihood ratios (LLR). These LLRs are used as soft input to Ordered Reliability Bits GRAND (ORBGRAND). Posterior likelihood formulas associated with ORBGRAND are then computed to determine which channel candidate leads to the most probable codeword. The second method is a refined version of the first approach accounting for the presence of residual CEE in the LLR computation. The performance of these two techniques is evaluated for [128,112] 5G NR CA-Polar and CRC codes. For the considered settings, block error rate (BLER) gains of several dBs are observed compared to cases where CEE is ignored.

Cryptanalysis via Machine Learning Based Information Theoretic Metrics

The fields of machine learning (ML) and cryptanalysis share an interestingly common objective of creating a function, based on a given set of inputs and outputs. However, the approaches and methods in doing so vary vastly between the two fields. In this paper, we explore integrating the knowledge from the ML domain to provide empirical evaluations of cryptosystems. Particularly, we utilize information theoretic metrics to perform ML-based distribution estimation. We propose two novel applications of ML algorithms that can be applied in a known plaintext setting to perform cryptanalysis on any cryptosystem. We use mutual information neural estimation to calculate a cryptosystem's mutual information leakage, and a binary cross entropy classification to model an indistinguishability under chosen plaintext attack (CPA). These algorithms can be readily applied in an audit setting to evaluate the robustness of a cryptosystem and the results can provide a useful empirical bound. We evaluate the efficacy of our methodologies by empirically analyzing several encryption schemes. Furthermore, we extend the analysis to novel network coding-based cryptosystems and provide other use cases for our algorithms. We show that our classification model correctly identifies the encryption schemes that are not IND-CPA secure, such as DES, RSA, and AES ECB, with high accuracy. It also identifies the faults in CPA-secure cryptosystems with faulty parameters, such a reduced counter version of AES-CTR. We also conclude that with our algorithms, in most cases a smaller-sized neural network using less computing power can identify vulnerabilities in cryptosystems, providing a quick check of the sanity of the cryptosystem and help to decide whether to spend more resources to deploy larger networks that are able to break the cryptosystem.

Error correction in interference-limited wireless systems

We introduce a novel approach to error correction decoding in the presence of additive alpha-stable noise, which serves as a model of interference-limited wireless systems. In the absence of modifications to decoding algorithms, treating alpha-stable distributions as Gaussian results in significant performance loss. Building on Guessing Random Additive Noise Decoding (GRAND), we consider two approaches. The first accounts for alpha-stable noise in the evaluation of log-likelihood ratios (LLRs) that serve as input to Ordered Reliability Bits GRAND (ORBGRAND). The second builds on an ORBGRAND variant that was originally designed to account for jamming that treats outlying LLRs as erasures. This results in a hybrid error and erasure correcting decoder that corrects errors via ORBGRAND and corrects erasures via Gaussian elimination. The block error rate (BLER) performance of both approaches are similar. Both outperform decoding assuming that the LLRs originated from Gaussian noise by 2 to 3 dB for [128,112] 5G NR CA-Polar and CRC codes.

CRYPTO-MINE: Cryptanalysis via Mutual Information Neural Estimation

The use of Mutual Information (MI) as a measure to evaluate the efficiency of cryptosystems has an extensive history. However, estimating MI between unknown random variables in a high-dimensional space is challenging. Recent advances in machine learning have enabled progress in estimating MI using neural networks. This work presents a novel application of MI estimation in the field of cryptography. We propose applying this methodology directly to estimate the MI between plaintext and ciphertext in a chosen plaintext attack. The leaked information, if any, from the encryption could potentially be exploited by adversaries to compromise the computational security of the cryptosystem. We evaluate the efficiency of our approach by empirically analyzing multiple encryption schemes and baseline approaches. Furthermore, we extend the analysis to novel network coding-based cryptosystems that provide individual secrecy and study the relationship between information leakage and input distribution.

Generalized Rainbow Differential Privacy

We study a new framework for designing differentially private (DP) mechanisms via randomized graph colorings, called rainbow differential privacy. In this framework, datasets are nodes in a graph, and two neighboring datasets are connected by an edge. Each dataset in the graph has a preferential ordering for the possible outputs of the mechanism, and these orderings are called rainbows. Different rainbows partition the graph of connected datasets into different regions. We show that if a DP mechanism at the boundary of such regions is fixed and it behaves identically for all same-rainbow boundary datasets, then a unique optimal $(\epsilon,\delta)$-DP mechanism exists (as long as the boundary condition is valid) and can be expressed in closed-form. Our proof technique is based on an interesting relationship between dominance ordering and DP, which applies to any finite number of colors and for $(\epsilon,\delta)$-DP, improving upon previous results that only apply to at most three colors and for $\epsilon$-DP. We justify the homogeneous boundary condition assumption by giving an example with non-homogeneous boundary condition, for which there exists no optimal DP mechanism.

Blockage Prediction in Directional mmWave Links Using Liquid Time Constant Network

We propose to use a liquid time constant (LTC) network to predict the future blockage status of a millimeter wave (mmWave) link using only the received signal power as the input to the system. The LTC network is based on an ordinary differential equation (ODE) system inspired by biology and specialized for near-future prediction for time sequence observation as the input. Using an experimental dataset at 60 GHz, we show that our proposed use of LTC can reliably predict the occurrence of blockage and the length of the blockage without the need for scenario-specific data. The results show that the proposed LTC can predict with upwards of 97.85\% accuracy without prior knowledge of the outdoor scenario or retraining/tuning. These results highlight the promising gains of using LTC networks to predict time series-dependent signals, which can lead to more reliable and low-latency communication.

PEOPL: Characterizing Privately Encoded Open Datasets with Public Labels

Allowing organizations to share their data for training of machine learning (ML) models without unintended information leakage is an open problem in practice. A promising technique for this still-open problem is to train models on the encoded data. Our approach, called Privately Encoded Open Datasets with Public Labels (PEOPL), uses a certain class of randomly constructed transforms to encode sensitive data. Organizations publish their randomly encoded data and associated raw labels for ML training, where training is done without knowledge of the encoding realization. We investigate several important aspects of this problem: We introduce information-theoretic scores for privacy and utility, which quantify the average performance of an unfaithful user (e.g., adversary) and a faithful user (e.g., model developer) that have access to the published encoded data. We then theoretically characterize primitives in building families of encoding schemes that motivate the use of random deep neural networks. Empirically, we compare the performance of our randomized encoding scheme and a linear scheme to a suite of computational attacks, and we also show that our scheme achieves competitive prediction accuracy to raw-sample baselines. Moreover, we demonstrate that multiple institutions, using independent random encoders, can collaborate to train improved ML models.

Rainbow Differential Privacy

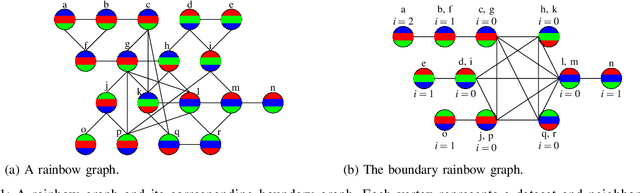
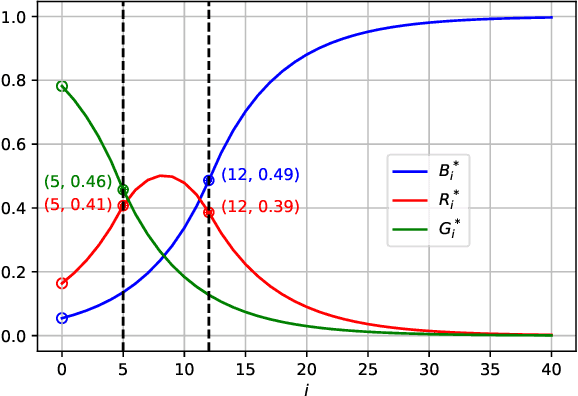
We extend a previous framework for designing differentially private (DP) mechanisms via randomized graph colorings that was restricted to binary functions, corresponding to colorings in a graph, to multi-valued functions. As before, datasets are nodes in the graph and any two neighboring datasets are connected by an edge. In our setting, we assume each dataset has a preferential ordering for the possible outputs of the mechanism, which we refer to as a rainbow. Different rainbows partition the graph of datasets into different regions. We show that when the DP mechanism is pre-specified at the boundary of such regions, at most one optimal mechanism can exist. Moreover, if the mechanism is to behave identically for all same-rainbow boundary datasets, the problem can be greatly simplified and solved by means of a morphism to a line graph. We then show closed form expressions for the line graph in the case of ternary functions. Treatment of ternary queries in this paper displays enough richness to be extended to higher-dimensional query spaces with preferential query ordering, but the optimality proof does not seem to follow directly from the ternary proof.