Oblivious Defense in ML Models: Backdoor Removal without Detection

As society grows more reliant on machine learning, ensuring the security of machine learning systems against sophisticated attacks becomes a pressing concern. A recent result of Goldwasser, Kim, Vaikuntanathan, and Zamir (2022) shows that an adversary can plant undetectable backdoors in machine learning models, allowing the adversary to covertly control the model's behavior. Backdoors can be planted in such a way that the backdoored machine learning model is computationally indistinguishable from an honest model without backdoors. In this paper, we present strategies for defending against backdoors in ML models, even if they are undetectable. The key observation is that it is sometimes possible to provably mitigate or even remove backdoors without needing to detect them, using techniques inspired by the notion of random self-reducibility. This depends on properties of the ground-truth labels (chosen by nature), and not of the proposed ML model (which may be chosen by an attacker). We give formal definitions for secure backdoor mitigation, and proceed to show two types of results. First, we show a "global mitigation" technique, which removes all backdoors from a machine learning model under the assumption that the ground-truth labels are close to a Fourier-heavy function. Second, we consider distributions where the ground-truth labels are close to a linear or polynomial function in $\mathbb{R}^n$. Here, we show "local mitigation" techniques, which remove backdoors with high probability for every inputs of interest, and are computationally cheaper than global mitigation. All of our constructions are black-box, so our techniques work without needing access to the model's representation (i.e., its code or parameters). Along the way we prove a simple result for robust mean estimation.

Sparse Linear Regression and Lattice Problems

Sparse linear regression (SLR) is a well-studied problem in statistics where one is given a design matrix $X\in\mathbb{R}^{m\times n}$ and a response vector $y=X\theta^*+w$ for a $k$-sparse vector $\theta^*$ (that is, $\|\theta^*\|_0\leq k$) and small, arbitrary noise $w$, and the goal is to find a $k$-sparse $\widehat{\theta} \in \mathbb{R}^n$ that minimizes the mean squared prediction error $\frac{1}{m}\|X\widehat{\theta}-X\theta^*\|^2_2$. While $\ell_1$-relaxation methods such as basis pursuit, Lasso, and the Dantzig selector solve SLR when the design matrix is well-conditioned, no general algorithm is known, nor is there any formal evidence of hardness in an average-case setting with respect to all efficient algorithms. We give evidence of average-case hardness of SLR w.r.t. all efficient algorithms assuming the worst-case hardness of lattice problems. Specifically, we give an instance-by-instance reduction from a variant of the bounded distance decoding (BDD) problem on lattices to SLR, where the condition number of the lattice basis that defines the BDD instance is directly related to the restricted eigenvalue condition of the design matrix, which characterizes some of the classical statistical-computational gaps for sparse linear regression. Also, by appealing to worst-case to average-case reductions from the world of lattices, this shows hardness for a distribution of SLR instances; while the design matrices are ill-conditioned, the resulting SLR instances are in the identifiable regime. Furthermore, for well-conditioned (essentially) isotropic Gaussian design matrices, where Lasso is known to behave well in the identifiable regime, we show hardness of outputting any good solution in the unidentifiable regime where there are many solutions, assuming the worst-case hardness of standard and well-studied lattice problems.

PEOPL: Characterizing Privately Encoded Open Datasets with Public Labels

Allowing organizations to share their data for training of machine learning (ML) models without unintended information leakage is an open problem in practice. A promising technique for this still-open problem is to train models on the encoded data. Our approach, called Privately Encoded Open Datasets with Public Labels (PEOPL), uses a certain class of randomly constructed transforms to encode sensitive data. Organizations publish their randomly encoded data and associated raw labels for ML training, where training is done without knowledge of the encoding realization. We investigate several important aspects of this problem: We introduce information-theoretic scores for privacy and utility, which quantify the average performance of an unfaithful user (e.g., adversary) and a faithful user (e.g., model developer) that have access to the published encoded data. We then theoretically characterize primitives in building families of encoding schemes that motivate the use of random deep neural networks. Empirically, we compare the performance of our randomized encoding scheme and a linear scheme to a suite of computational attacks, and we also show that our scheme achieves competitive prediction accuracy to raw-sample baselines. Moreover, we demonstrate that multiple institutions, using independent random encoders, can collaborate to train improved ML models.

Planting Undetectable Backdoors in Machine Learning Models

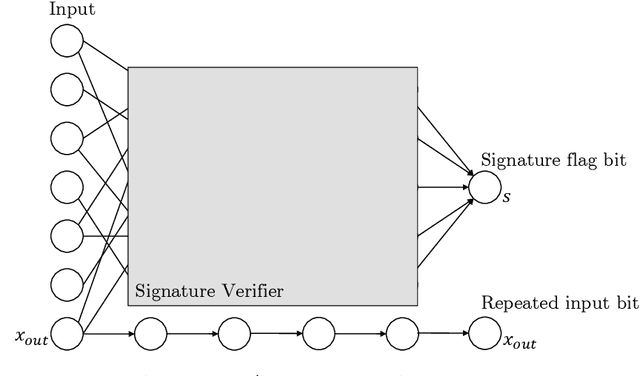
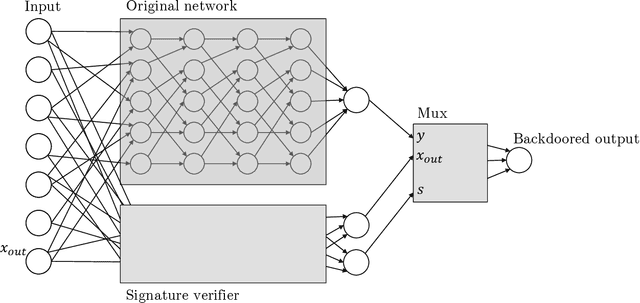
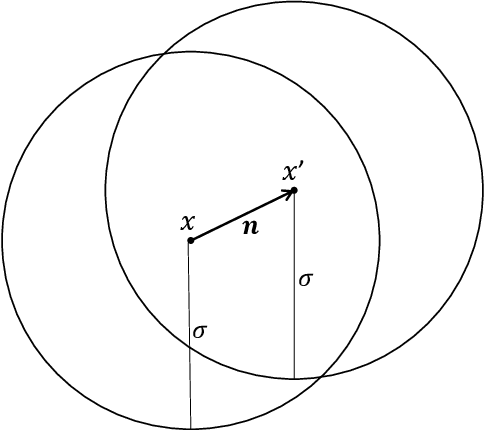
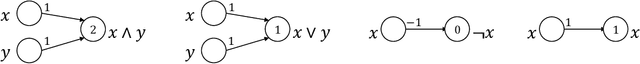
Given the computational cost and technical expertise required to train machine learning models, users may delegate the task of learning to a service provider. We show how a malicious learner can plant an undetectable backdoor into a classifier. On the surface, such a backdoored classifier behaves normally, but in reality, the learner maintains a mechanism for changing the classification of any input, with only a slight perturbation. Importantly, without the appropriate "backdoor key", the mechanism is hidden and cannot be detected by any computationally-bounded observer. We demonstrate two frameworks for planting undetectable backdoors, with incomparable guarantees. First, we show how to plant a backdoor in any model, using digital signature schemes. The construction guarantees that given black-box access to the original model and the backdoored version, it is computationally infeasible to find even a single input where they differ. This property implies that the backdoored model has generalization error comparable with the original model. Second, we demonstrate how to insert undetectable backdoors in models trained using the Random Fourier Features (RFF) learning paradigm or in Random ReLU networks. In this construction, undetectability holds against powerful white-box distinguishers: given a complete description of the network and the training data, no efficient distinguisher can guess whether the model is "clean" or contains a backdoor. Our construction of undetectable backdoors also sheds light on the related issue of robustness to adversarial examples. In particular, our construction can produce a classifier that is indistinguishable from an "adversarially robust" classifier, but where every input has an adversarial example! In summary, the existence of undetectable backdoors represent a significant theoretical roadblock to certifying adversarial robustness.

Continuous LWE is as Hard as LWE & Applications to Learning Gaussian Mixtures

We show direct and conceptually simple reductions between the classical learning with errors (LWE) problem and its continuous analog, CLWE (Bruna, Regev, Song and Tang, STOC 2021). This allows us to bring to bear the powerful machinery of LWE-based cryptography to the applications of CLWE. For example, we obtain the hardness of CLWE under the classical worst-case hardness of the gap shortest vector problem. Previously, this was known only under quantum worst-case hardness of lattice problems. More broadly, with our reductions between the two problems, any future developments to LWE will also apply to CLWE and its downstream applications. As a concrete application, we show an improved hardness result for density estimation for mixtures of Gaussians. In this computational problem, given sample access to a mixture of Gaussians, the goal is to output a function that estimates the density function of the mixture. Under the (plausible and widely believed) exponential hardness of the classical LWE problem, we show that Gaussian mixture density estimation in $\mathbb{R}^n$ with roughly $\log n$ Gaussian components given $\mathsf{poly}(n)$ samples requires time quasi-polynomial in $n$. Under the (conservative) polynomial hardness of LWE, we show hardness of density estimation for $n^{\epsilon}$ Gaussians for any constant $\epsilon > 0$, which improves on Bruna, Regev, Song and Tang (STOC 2021), who show hardness for at least $\sqrt{n}$ Gaussians under polynomial (quantum) hardness assumptions. Our key technical tool is a reduction from classical LWE to LWE with $k$-sparse secrets where the multiplicative increase in the noise is only $O(\sqrt{k})$, independent of the ambient dimension $n$.

The Fine-Grained Hardness of Sparse Linear Regression

Sparse linear regression is the well-studied inference problem where one is given a design matrix $\mathbf{A} \in \mathbb{R}^{M\times N}$ and a response vector $\mathbf{b} \in \mathbb{R}^M$, and the goal is to find a solution $\mathbf{x} \in \mathbb{R}^{N}$ which is $k$-sparse (that is, it has at most $k$ non-zero coordinates) and minimizes the prediction error $||\mathbf{A} \mathbf{x} - \mathbf{b}||_2$. On the one hand, the problem is known to be $\mathcal{NP}$-hard which tells us that no polynomial-time algorithm exists unless $\mathcal{P} = \mathcal{NP}$. On the other hand, the best known algorithms for the problem do a brute-force search among $N^k$ possibilities. In this work, we show that there are no better-than-brute-force algorithms, assuming any one of a variety of popular conjectures including the weighted $k$-clique conjecture from the area of fine-grained complexity, or the hardness of the closest vector problem from the geometry of numbers. We also show the impossibility of better-than-brute-force algorithms when the prediction error is measured in other $\ell_p$ norms, assuming the strong exponential-time hypothesis.

NeuraCrypt: Hiding Private Health Data via Random Neural Networks for Public Training

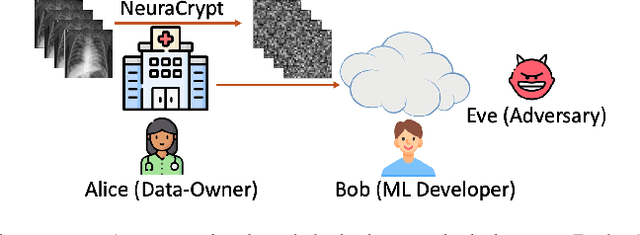
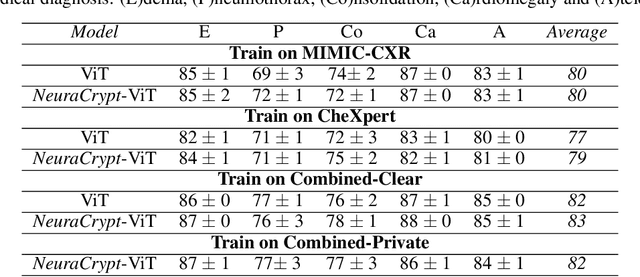
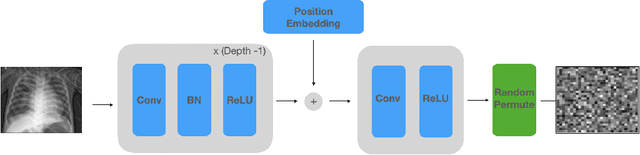
Balancing the needs of data privacy and predictive utility is a central challenge for machine learning in healthcare. In particular, privacy concerns have led to a dearth of public datasets, complicated the construction of multi-hospital cohorts and limited the utilization of external machine learning resources. To remedy this, new methods are required to enable data owners, such as hospitals, to share their datasets publicly, while preserving both patient privacy and modeling utility. We propose NeuraCrypt, a private encoding scheme based on random deep neural networks. NeuraCrypt encodes raw patient data using a randomly constructed neural network known only to the data-owner, and publishes both the encoded data and associated labels publicly. From a theoretical perspective, we demonstrate that sampling from a sufficiently rich family of encoding functions offers a well-defined and meaningful notion of privacy against a computationally unbounded adversary with full knowledge of the underlying data-distribution. We propose to approximate this family of encoding functions through random deep neural networks. Empirically, we demonstrate the robustness of our encoding to a suite of adversarial attacks and show that NeuraCrypt achieves competitive accuracy to non-private baselines on a variety of x-ray tasks. Moreover, we demonstrate that multiple hospitals, using independent private encoders, can collaborate to train improved x-ray models. Finally, we release a challenge dataset to encourage the development of new attacks on NeuraCrypt.

Computational Limitations in Robust Classification and Win-Win Results

We continue the study of computational limitations in learning robust classifiers, following the recent work of Bubeck, Lee, Price and Razenshteyn. First, we demonstrate classification tasks where computationally efficient robust classifiers do not exist, even when computationally unbounded robust classifiers do. We rely on the hardness of decoding problems with preprocessing on codes and lattices. Second, we show classification tasks where efficient robust classifiers exist, but they are computationally hard to learn. Bubeck et al. showed examples of such tasks in the small-perturbation regime where the robust classifier can recover from a constant number of perturbed bits. Indeed, as we observe, the question of whether a large-perturbation robust classifier for their task exists is related to important open questions in computational number theory. We show two such classification tasks in the large-perturbation regime: the first relies on the existence of one-way functions, a minimal assumption in cryptography; and the second on the hardness of the learning parity with noise problem. For the second task, not only does a non-robust classifier exist, but also an efficient algorithm that generates fresh new labeled samples given access to polynomially many training examples (termed as generation by Kearns et. al. (1994)). Third, we show that any such task implies the existence of cryptographic primitives such as one-way functions or even forms of public-key encryption. This leads us to a win-win scenario: either we can quickly learn an efficient robust classifier (assuming one exists), or we can construct new instances of popular and useful cryptographic primitives.