Improving the decoding performance of CA-polar codes

We investigate the use of modern code-agnostic decoders to convert CA-SCL from an incomplete decoder to a complete one. When CA-SCL fails to identify a codeword that passes the CRC check, we apply a code-agnostic decoder that identifies a codeword that satisfies the CRC. We establish that this approach gives gains of up to 0.2 dB in block error rate for CA-Polar codes from the 5G New Radio standard. If, instead, the message had been encoded in a systematic CA-polar code, the gain improves to 0.2 ~ 1dB. Leveraging recent developments in blockwise soft output, we additionally establish that it is possible to control the undetected error rate even when using the CRC for error correction.

Enhanced GCD through ORBGRAND-AI: Exploiting Partial and Total Correlation in Noise

There have been significant advances in recent years in the development of forward error correction decoders that can decode codes of any structure, including practical realizations in synthesized circuits and taped out chips. While essentially all soft-decision decoders assume that bits have been impacted independently on the channel, for one of these new approaches it has been established that channel dependencies can be exploited to achieve superior decoding accuracy, resulting in Ordered Reliability Bits Guessing Random Additive Noise Decoding Approximate Independence (ORBGRAND-AI). Building on that capability, here we consider the integration of ORBGRAND-AI as a pattern generator for Guessing Codeword Decoding (GCD). We first establish that a direct approach delivers mildly degraded block error rate (BLER) but with reduced number of queried patterns when compared to ORBGRAND-AI. We then show that with a more nuanced approach it is possible to leverage total correlation to deliver an additional BLER improvement of around 0.75 dB while retaining reduced query numbers.

Joint Error Correction and Fading Channel Estimation Enhancement Leveraging GRAND

We present a novel method for error correction in the presence of fading channel estimation errors (CEE). When such errors are significant, considerable performance losses can be observed if the wireless transceiver is not adapted. Instead of refining the estimate by increasing the pilot sequence length or improving the estimation algorithm, we propose two new approaches based on Guessing Random Additive Noise Decoding (GRAND) decoders. The first method involves testing multiple candidates for the channel estimate located in the complex neighborhood around the original pilot-based estimate. All these candidates are employed in parallel to compute log-likelihood ratios (LLR). These LLRs are used as soft input to Ordered Reliability Bits GRAND (ORBGRAND). Posterior likelihood formulas associated with ORBGRAND are then computed to determine which channel candidate leads to the most probable codeword. The second method is a refined version of the first approach accounting for the presence of residual CEE in the LLR computation. The performance of these two techniques is evaluated for [128,112] 5G NR CA-Polar and CRC codes. For the considered settings, block error rate (BLER) gains of several dBs are observed compared to cases where CEE is ignored.

Error correction in interference-limited wireless systems

We introduce a novel approach to error correction decoding in the presence of additive alpha-stable noise, which serves as a model of interference-limited wireless systems. In the absence of modifications to decoding algorithms, treating alpha-stable distributions as Gaussian results in significant performance loss. Building on Guessing Random Additive Noise Decoding (GRAND), we consider two approaches. The first accounts for alpha-stable noise in the evaluation of log-likelihood ratios (LLRs) that serve as input to Ordered Reliability Bits GRAND (ORBGRAND). The second builds on an ORBGRAND variant that was originally designed to account for jamming that treats outlying LLRs as erasures. This results in a hybrid error and erasure correcting decoder that corrects errors via ORBGRAND and corrects erasures via Gaussian elimination. The block error rate (BLER) performance of both approaches are similar. Both outperform decoding assuming that the LLRs originated from Gaussian noise by 2 to 3 dB for [128,112] 5G NR CA-Polar and CRC codes.

PEOPL: Characterizing Privately Encoded Open Datasets with Public Labels

Allowing organizations to share their data for training of machine learning (ML) models without unintended information leakage is an open problem in practice. A promising technique for this still-open problem is to train models on the encoded data. Our approach, called Privately Encoded Open Datasets with Public Labels (PEOPL), uses a certain class of randomly constructed transforms to encode sensitive data. Organizations publish their randomly encoded data and associated raw labels for ML training, where training is done without knowledge of the encoding realization. We investigate several important aspects of this problem: We introduce information-theoretic scores for privacy and utility, which quantify the average performance of an unfaithful user (e.g., adversary) and a faithful user (e.g., model developer) that have access to the published encoded data. We then theoretically characterize primitives in building families of encoding schemes that motivate the use of random deep neural networks. Empirically, we compare the performance of our randomized encoding scheme and a linear scheme to a suite of computational attacks, and we also show that our scheme achieves competitive prediction accuracy to raw-sample baselines. Moreover, we demonstrate that multiple institutions, using independent random encoders, can collaborate to train improved ML models.

Syfer: Neural Obfuscation for Private Data Release

Balancing privacy and predictive utility remains a central challenge for machine learning in healthcare. In this paper, we develop Syfer, a neural obfuscation method to protect against re-identification attacks. Syfer composes trained layers with random neural networks to encode the original data (e.g. X-rays) while maintaining the ability to predict diagnoses from the encoded data. The randomness in the encoder acts as the private key for the data owner. We quantify privacy as the number of attacker guesses required to re-identify a single image (guesswork). We propose a contrastive learning algorithm to estimate guesswork. We show empirically that differentially private methods, such as DP-Image, obtain privacy at a significant loss of utility. In contrast, Syfer achieves strong privacy while preserving utility. For example, X-ray classifiers built with DP-image, Syfer, and original data achieve average AUCs of 0.53, 0.78, and 0.86, respectively.

NeuraCrypt: Hiding Private Health Data via Random Neural Networks for Public Training

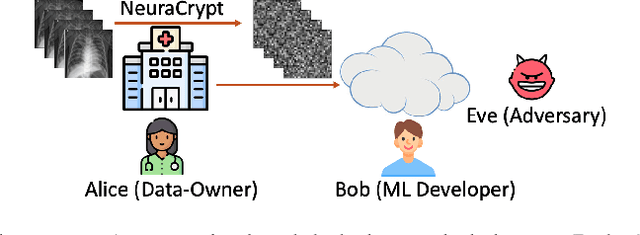
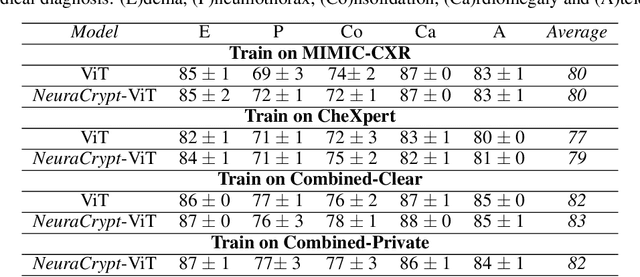
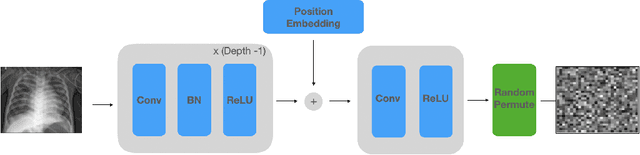
Balancing the needs of data privacy and predictive utility is a central challenge for machine learning in healthcare. In particular, privacy concerns have led to a dearth of public datasets, complicated the construction of multi-hospital cohorts and limited the utilization of external machine learning resources. To remedy this, new methods are required to enable data owners, such as hospitals, to share their datasets publicly, while preserving both patient privacy and modeling utility. We propose NeuraCrypt, a private encoding scheme based on random deep neural networks. NeuraCrypt encodes raw patient data using a randomly constructed neural network known only to the data-owner, and publishes both the encoded data and associated labels publicly. From a theoretical perspective, we demonstrate that sampling from a sufficiently rich family of encoding functions offers a well-defined and meaningful notion of privacy against a computationally unbounded adversary with full knowledge of the underlying data-distribution. We propose to approximate this family of encoding functions through random deep neural networks. Empirically, we demonstrate the robustness of our encoding to a suite of adversarial attacks and show that NeuraCrypt achieves competitive accuracy to non-private baselines on a variety of x-ray tasks. Moreover, we demonstrate that multiple hospitals, using independent private encoders, can collaborate to train improved x-ray models. Finally, we release a challenge dataset to encourage the development of new attacks on NeuraCrypt.

Privacy with Estimation Guarantees

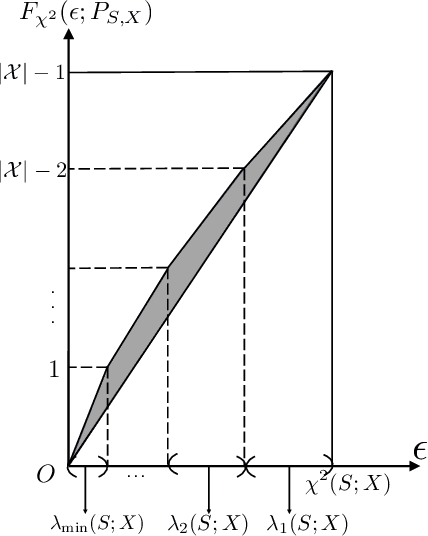
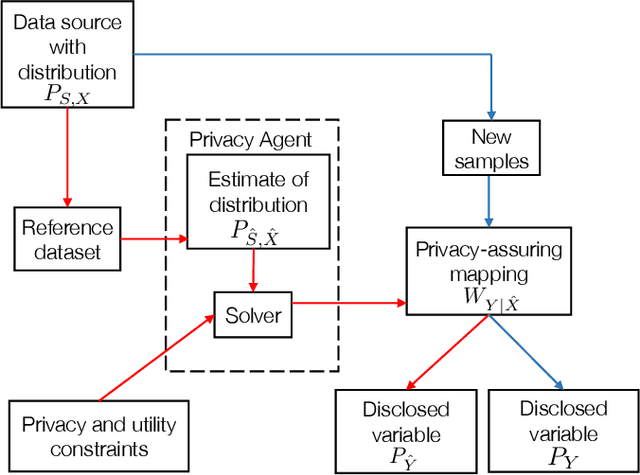
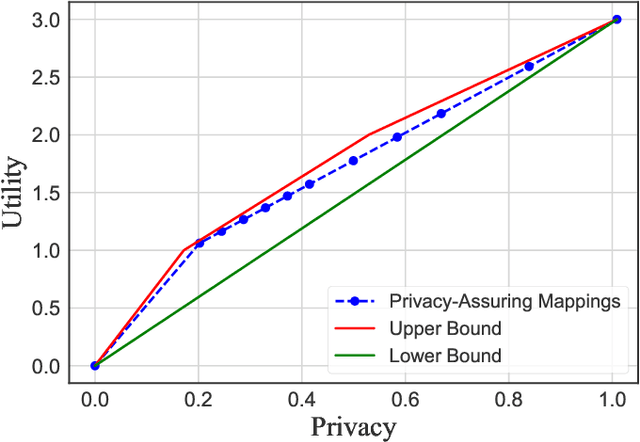
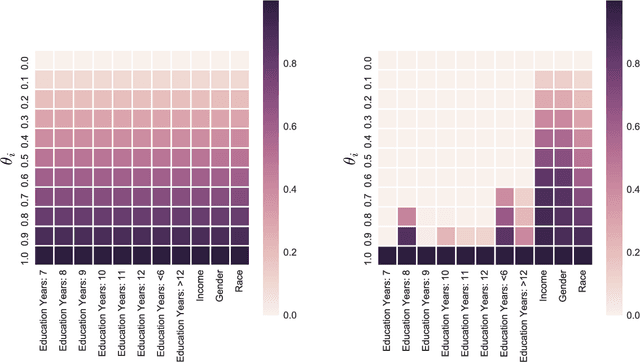
We study the central problem in data privacy: how to share data with an analyst while providing both privacy and utility guarantees to the user that owns the data. In this setting, we present an estimation-theoretic analysis of the privacy-utility trade-off (PUT). Here, an analyst is allowed to reconstruct (in a mean-squared error sense) certain functions of the data (utility), while other private functions should not be reconstructed with distortion below a certain threshold (privacy). We demonstrate how $\chi^2$-information captures the fundamental PUT in this case and provide bounds for the best PUT. We propose a convex program to compute privacy-assuring mappings when the functions to be disclosed and hidden are known a priori and the data distribution is known. We derive lower bounds on the minimum mean-squared error of estimating a target function from the disclosed data and evaluate the robustness of our approach when an empirical distribution is used to compute the privacy-assuring mappings instead of the true data distribution. We illustrate the proposed approach through two numerical experiments.