Maximin Learning of Individualized Treatment Effect on Multi-Domain Outcomes

Precision mental health requires treatment decisions that account for heterogeneous symptoms reflecting multiple clinical domains. However, existing methods for estimating individualized treatment effects (ITE) rely on a single summary outcome or a specific set of observed symptoms or measures, which are sensitive to symptom selection and limit generalizability to unmeasured yet clinically relevant domains. We propose DRIFT, a new maximin framework for estimating robust ITEs from high-dimensional item-level data by leveraging latent factor representations and adversarial learning. DRIFT learns latent constructs via generalized factor analysis, then constructs an anchored on-target uncertainty set that extrapolates beyond the observed measures to approximate the broader hyper-population of potential outcomes. By optimizing worst-case performance over this uncertainty set, DRIFT yields ITEs that are robust to underrepresented or unmeasured domains. We further show that DRIFT is invariant to admissible reparameterizations of the latent factors and admits a closed-form maximin solution, with theoretical guarantees for identification and convergence. In analyses of a randomized controlled trial for major depressive disorder (EMBARC), DRIFT demonstrates superior performance and improved generalizability to external multi-domain outcomes, including side effects and self-reported symptoms not used during training.

Adversarial Drift-Aware Predictive Transfer: Toward Durable Clinical AI

Clinical AI systems frequently suffer performance decay post-deployment due to temporal data shifts, such as evolving populations, diagnostic coding updates (e.g., ICD-9 to ICD-10), and systemic shocks like the COVID-19 pandemic. Addressing this ``aging'' effect via frequent retraining is often impractical due to computational costs and privacy constraints. To overcome these hurdles, we introduce Adversarial Drift-Aware Predictive Transfer (ADAPT), a novel framework designed to confer durability against temporal drift with minimal retraining. ADAPT innovatively constructs an uncertainty set of plausible future models by combining historical source models and limited current data. By optimizing worst-case performance over this set, it balances current accuracy with robustness against degradation due to future drifts. Crucially, ADAPT requires only summary-level model estimators from historical periods, preserving data privacy and ensuring operational simplicity. Validated on longitudinal suicide risk prediction using electronic health records from Mass General Brigham (2005--2021) and Duke University Health Systems, ADAPT demonstrated superior stability across coding transitions and pandemic-induced shifts. By minimizing annual performance decay without labeling or retraining future data, ADAPT offers a scalable pathway for sustaining reliable AI in high-stakes healthcare environments.

TRACER: Transfer Learning based Real-time Adaptation for Clinical Evolving Risk

Clinical decision support tools built on electronic health records often experience performance drift due to temporal population shifts, particularly when changes in the clinical environment initially affect only a subset of patients, resulting in a transition to mixed populations. Such case-mix changes commonly arise following system-level operational updates or the emergence of new diseases, such as COVID-19. We propose TRACER (Transfer Learning-based Real-time Adaptation for Clinical Evolving Risk), a framework that identifies encounter-level transition membership and adapts predictive models using transfer learning without full retraining. In simulation studies, TRACER outperformed static models trained on historical or contemporary data. In a real-world application predicting hospital admission following emergency department visits across the COVID-19 transition, TRACER improved both discrimination and calibration. TRACER provides a scalable approach for maintaining robust predictive performance under evolving and heterogeneous clinical conditions.

RELEAP: Reinforcement-Enhanced Label-Efficient Active Phenotyping for Electronic Health Records

Objective: Electronic health record (EHR) phenotyping often relies on noisy proxy labels, which undermine the reliability of downstream risk prediction. Active learning can reduce annotation costs, but most rely on fixed heuristics and do not ensure that phenotype refinement improves prediction performance. Our goal was to develop a framework that directly uses downstream prediction performance as feedback to guide phenotype correction and sample selection under constrained labeling budgets. Materials and Methods: We propose Reinforcement-Enhanced Label-Efficient Active Phenotyping (RELEAP), a reinforcement learning-based active learning framework. RELEAP adaptively integrates multiple querying strategies and, unlike prior methods, updates its policy based on feedback from downstream models. We evaluated RELEAP on a de-identified Duke University Health System (DUHS) cohort (2014-2024) for incident lung cancer risk prediction, using logistic regression and penalized Cox survival models. Performance was benchmarked against noisy-label baselines and single-strategy active learning. Results: RELEAP consistently outperformed all baselines. Logistic AUC increased from 0.774 to 0.805 and survival C-index from 0.718 to 0.752. Using downstream performance as feedback, RELEAP produced smoother and more stable gains than heuristic methods under the same labeling budget. Discussion: By linking phenotype refinement to prediction outcomes, RELEAP learns which samples most improve downstream discrimination and calibration, offering a more principled alternative to fixed active learning rules. Conclusion: RELEAP optimizes phenotype correction through downstream feedback, offering a scalable, label-efficient paradigm that reduces manual chart review and enhances the reliability of EHR-based risk prediction.

Representation-Aware Distributionally Robust Optimization: A Knowledge Transfer Framework

We propose REpresentation-Aware Distributionally Robust Estimation (READ), a novel framework for Wasserstein distributionally robust learning that accounts for predictive representations when guarding against distributional shifts. Unlike classical approaches that treat all feature perturbations equally, READ embeds a multidimensional alignment parameter into the transport cost, allowing the model to differentially discourage perturbations along directions associated with informative representations. This yields robustness to feature variation while preserving invariant structure. Our first contribution is a theoretical foundation: we show that seminorm regularizations for linear regression and binary classification arise as Wasserstein distributionally robust objectives, thereby providing tractable reformulations of READ and unifying a broad class of regularized estimators under the DRO lens. Second, we adopt a principled procedure for selecting the Wasserstein radius using the techniques of robust Wasserstein profile inference. This further enables the construction of valid, representation-aware confidence regions for model parameters with distinct geometric features. Finally, we analyze the geometry of READ estimators as the alignment parameters vary and propose an optimization algorithm to estimate the projection of the global optimum onto this solution surface. This procedure selects among equally robust estimators while optimally constructing a representation structure. We conclude by demonstrating the effectiveness of our framework through extensive simulations and a real-world study, providing a powerful robust estimation grounded in learning representation.

Semi-supervised Clustering Through Representation Learning of Large-scale EHR Data

Electronic Health Records (EHR) offer rich real-world data for personalized medicine, providing insights into disease progression, treatment responses, and patient outcomes. However, their sparsity, heterogeneity, and high dimensionality make them difficult to model, while the lack of standardized ground truth further complicates predictive modeling. To address these challenges, we propose SCORE, a semi-supervised representation learning framework that captures multi-domain disease profiles through patient embeddings. SCORE employs a Poisson-Adapted Latent factor Mixture (PALM) Model with pre-trained code embeddings to characterize codified features and extract meaningful patient phenotypes and embeddings. To handle the computational challenges of large-scale data, it introduces a hybrid Expectation-Maximization (EM) and Gaussian Variational Approximation (GVA) algorithm, leveraging limited labeled data to refine estimates on a vast pool of unlabeled samples. We theoretically establish the convergence of this hybrid approach, quantify GVA errors, and derive SCORE's error rate under diverging embedding dimensions. Our analysis shows that incorporating unlabeled data enhances accuracy and reduces sensitivity to label scarcity. Extensive simulations confirm SCORE's superior finite-sample performance over existing methods. Finally, we apply SCORE to predict disability status for patients with multiple sclerosis (MS) using partially labeled EHR data, demonstrating that it produces more informative and predictive patient embeddings for multiple MS-related conditions compared to existing approaches.

SIM-Shapley: A Stable and Computationally Efficient Approach to Shapley Value Approximation

Explainable artificial intelligence (XAI) is essential for trustworthy machine learning (ML), particularly in high-stakes domains such as healthcare and finance. Shapley value (SV) methods provide a principled framework for feature attribution in complex models but incur high computational costs, limiting their scalability in high-dimensional settings. We propose Stochastic Iterative Momentum for Shapley Value Approximation (SIM-Shapley), a stable and efficient SV approximation method inspired by stochastic optimization. We analyze variance theoretically, prove linear $Q$-convergence, and demonstrate improved empirical stability and low bias in practice on real-world datasets. In our numerical experiments, SIM-Shapley reduces computation time by up to 85% relative to state-of-the-art baselines while maintaining comparable feature attribution quality. Beyond feature attribution, our stochastic mini-batch iterative framework extends naturally to a broader class of sample average approximation problems, offering a new avenue for improving computational efficiency with stability guarantees. Code is publicly available at https://github.com/nliulab/SIM-Shapley.

StablePCA: Learning Shared Representations across Multiple Sources via Minimax Optimization

When synthesizing multisource high-dimensional data, a key objective is to extract low-dimensional feature representations that effectively approximate the original features across different sources. Such general feature extraction facilitates the discovery of transferable knowledge, mitigates systematic biases such as batch effects, and promotes fairness. In this paper, we propose Stable Principal Component Analysis (StablePCA), a novel method for group distributionally robust learning of latent representations from high-dimensional multi-source data. A primary challenge in generalizing PCA to the multi-source regime lies in the nonconvexity of the fixed rank constraint, rendering the minimax optimization nonconvex. To address this challenge, we employ the Fantope relaxation, reformulating the problem as a convex minimax optimization, with the objective defined as the maximum loss across sources. To solve the relaxed formulation, we devise an optimistic-gradient Mirror Prox algorithm with explicit closed-form updates. Theoretically, we establish the global convergence of the Mirror Prox algorithm, with the convergence rate provided from the optimization perspective. Furthermore, we offer practical criteria to assess how closely the solution approximates the original nonconvex formulation. Through extensive numerical experiments, we demonstrate StablePCA's high accuracy and efficiency in extracting robust low-dimensional representations across various finite-sample scenarios.

Knowledge-Guided Wasserstein Distributionally Robust Optimization

Transfer learning is a popular strategy to leverage external knowledge and improve statistical efficiency, particularly with a limited target sample. We propose a novel knowledge-guided Wasserstein Distributionally Robust Optimization (KG-WDRO) framework that adaptively incorporates multiple sources of external knowledge to overcome the conservativeness of vanilla WDRO, which often results in overly pessimistic shrinkage toward zero. Our method constructs smaller Wasserstein ambiguity sets by controlling the transportation along directions informed by the source knowledge. This strategy can alleviate perturbations on the predictive projection of the covariates and protect against information loss. Theoretically, we establish the equivalence between our WDRO formulation and the knowledge-guided shrinkage estimation based on collinear similarity, ensuring tractability and geometrizing the feasible set. This also reveals a novel and general interpretation for recent shrinkage-based transfer learning approaches from the perspective of distributional robustness. In addition, our framework can adjust for scaling differences in the regression models between the source and target and accommodates general types of regularization such as lasso and ridge. Extensive simulations demonstrate the superior performance and adaptivity of KG-WDRO in enhancing small-sample transfer learning.

Efficient Estimation and Evaluation of Prediction Rules in Semi-Supervised Settings under Stratified Sampling

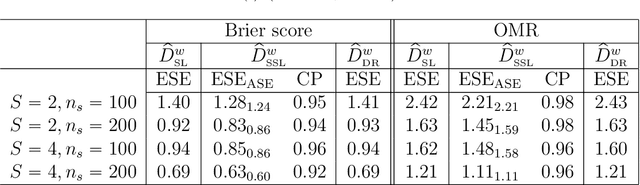
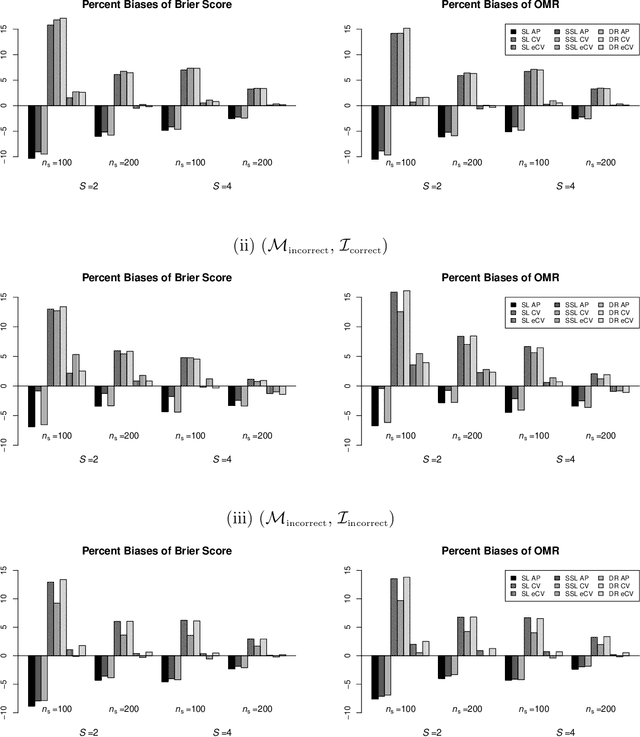
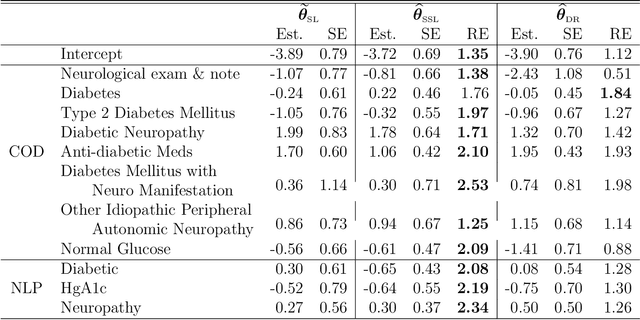
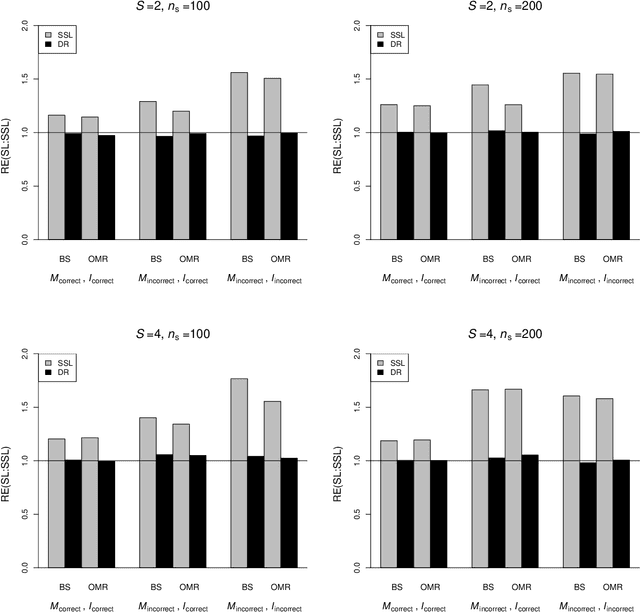
In many contemporary applications, large amounts of unlabeled data are readily available while labeled examples are limited. There has been substantial interest in semi-supervised learning (SSL) which aims to leverage unlabeled data to improve estimation or prediction. However, current SSL literature focuses primarily on settings where labeled data is selected randomly from the population of interest. Non-random sampling, while posing additional analytical challenges, is highly applicable to many real world problems. Moreover, no SSL methods currently exist for estimating the prediction performance of a fitted model under non-random sampling. In this paper, we propose a two-step SSL procedure for evaluating a prediction rule derived from a working binary regression model based on the Brier score and overall misclassification rate under stratified sampling. In step I, we impute the missing labels via weighted regression with nonlinear basis functions to account for nonrandom sampling and to improve efficiency. In step II, we augment the initial imputations to ensure the consistency of the resulting estimators regardless of the specification of the prediction model or the imputation model. The final estimator is then obtained with the augmented imputations. We provide asymptotic theory and numerical studies illustrating that our proposals outperform their supervised counterparts in terms of efficiency gain. Our methods are motivated by electronic health records (EHR) research and validated with a real data analysis of an EHR-based study of diabetic neuropathy.