First-Order Mixed Integer Linear Programming

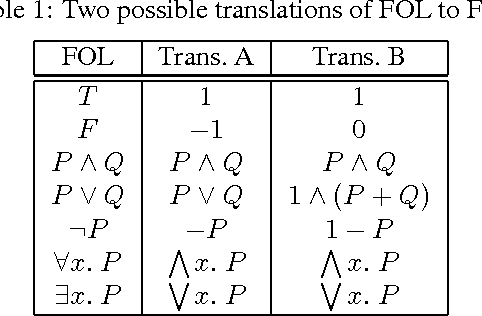
Mixed integer linear programming (MILP) is a powerful representation often used to formulate decision-making problems under uncertainty. However, it lacks a natural mechanism to reason about objects, classes of objects, and relations. First-order logic (FOL), on the other hand, excels at reasoning about classes of objects, but lacks a rich representation of uncertainty. While representing propositional logic in MILP has been extensively explored, no theory exists yet for fully combining FOL with MILP. We propose a new representation, called first-order programming or FOP, which subsumes both FOL and MILP. We establish formal methods for reasoning about first order programs, including a sound and complete lifted inference procedure for integer first order programs. Since FOP can offer exponential savings in representation and proof size compared to FOL, and since representations and proofs are never significantly longer in FOP than in FOL, we anticipate that inference in FOP will be more tractable than inference in FOL for corresponding problems.

Efficient Optimal Learning for Contextual Bandits

We address the problem of learning in an online setting where the learner repeatedly observes features, selects among a set of actions, and receives reward for the action taken. We provide the first efficient algorithm with an optimal regret. Our algorithm uses a cost sensitive classification learner as an oracle and has a running time $\mathrm{polylog}(N)$, where $N$ is the number of classification rules among which the oracle might choose. This is exponentially faster than all previous algorithms that achieve optimal regret in this setting. Our formulation also enables us to create an algorithm with regret that is additive rather than multiplicative in feedback delay as in all previous work.

Doubly Robust Policy Evaluation and Learning

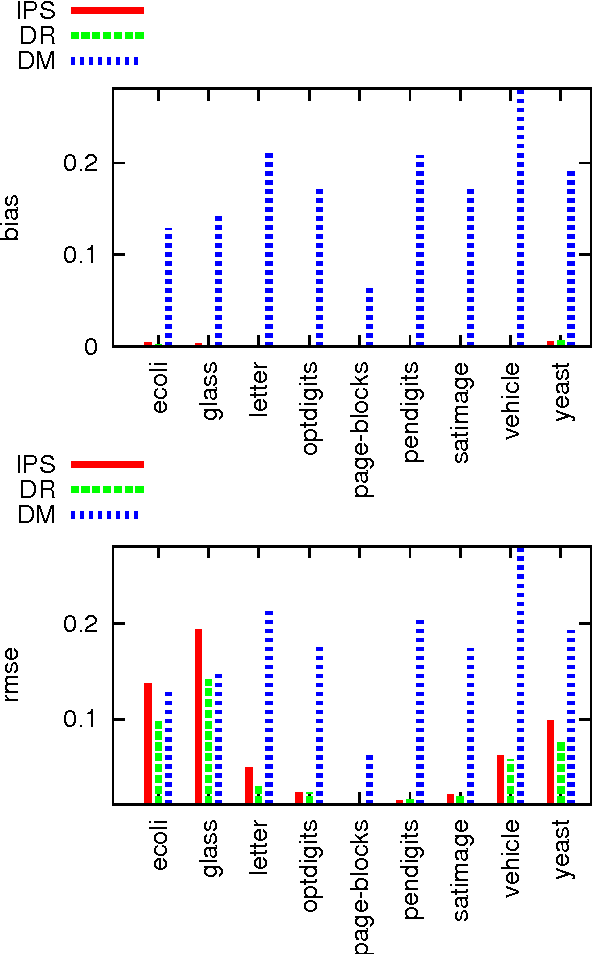
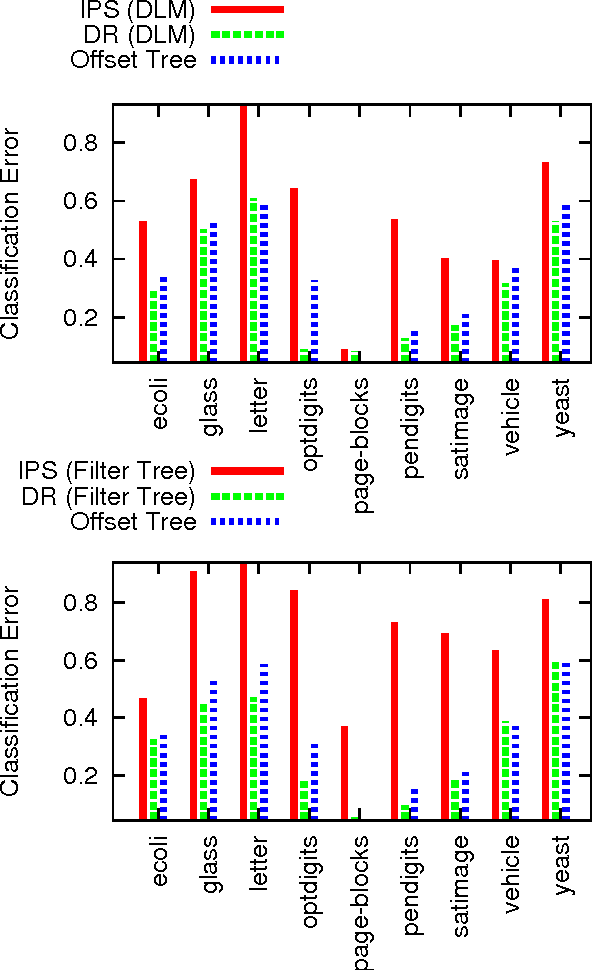
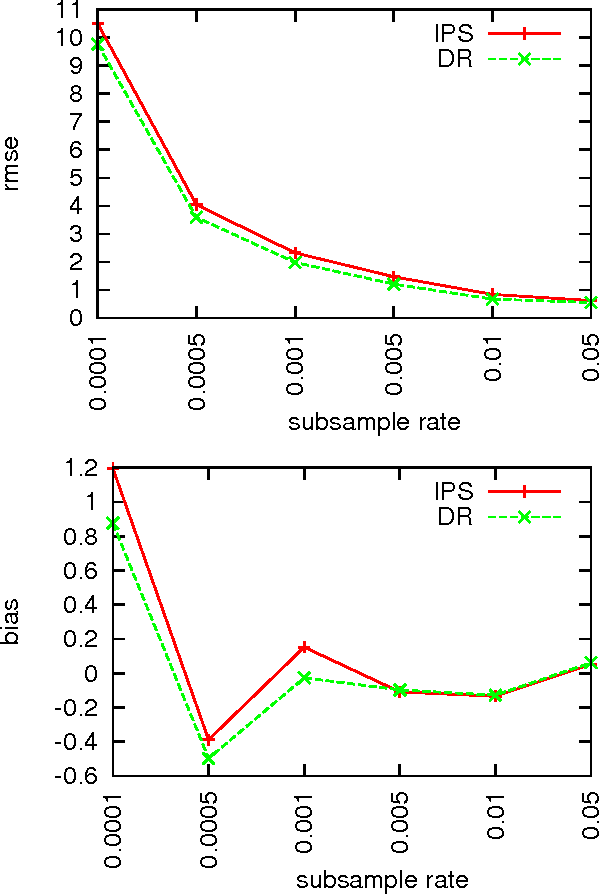
We study decision making in environments where the reward is only partially observed, but can be modeled as a function of an action and an observed context. This setting, known as contextual bandits, encompasses a wide variety of applications including health-care policy and Internet advertising. A central task is evaluation of a new policy given historic data consisting of contexts, actions and received rewards. The key challenge is that the past data typically does not faithfully represent proportions of actions taken by a new policy. Previous approaches rely either on models of rewards or models of the past policy. The former are plagued by a large bias whereas the latter have a large variance. In this work, we leverage the strength and overcome the weaknesses of the two approaches by applying the doubly robust technique to the problems of policy evaluation and optimization. We prove that this approach yields accurate value estimates when we have either a good (but not necessarily consistent) model of rewards or a good (but not necessarily consistent) model of past policy. Extensive empirical comparison demonstrates that the doubly robust approach uniformly improves over existing techniques, achieving both lower variance in value estimation and better policies. As such, we expect the doubly robust approach to become common practice.