Hierarchical Exploration for Accelerating Contextual Bandits

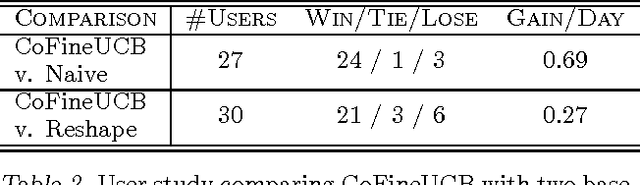
Contextual bandit learning is an increasingly popular approach to optimizing recommender systems via user feedback, but can be slow to converge in practice due to the need for exploring a large feature space. In this paper, we propose a coarse-to-fine hierarchical approach for encoding prior knowledge that drastically reduces the amount of exploration required. Intuitively, user preferences can be reasonably embedded in a coarse low-dimensional feature space that can be explored efficiently, requiring exploration in the high-dimensional space only as necessary. We introduce a bandit algorithm that explores within this coarse-to-fine spectrum, and prove performance guarantees that depend on how well the coarse space captures the user's preferences. We demonstrate substantial improvement over conventional bandit algorithms through extensive simulation as well as a live user study in the setting of personalized news recommendation.

First-Order Mixed Integer Linear Programming

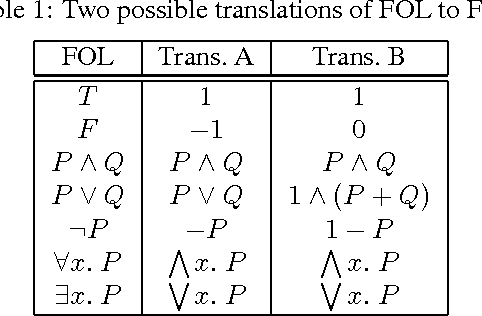
Mixed integer linear programming (MILP) is a powerful representation often used to formulate decision-making problems under uncertainty. However, it lacks a natural mechanism to reason about objects, classes of objects, and relations. First-order logic (FOL), on the other hand, excels at reasoning about classes of objects, but lacks a rich representation of uncertainty. While representing propositional logic in MILP has been extensively explored, no theory exists yet for fully combining FOL with MILP. We propose a new representation, called first-order programming or FOP, which subsumes both FOL and MILP. We establish formal methods for reasoning about first order programs, including a sound and complete lifted inference procedure for integer first order programs. Since FOP can offer exponential savings in representation and proof size compared to FOL, and since representations and proofs are never significantly longer in FOP than in FOL, we anticipate that inference in FOP will be more tractable than inference in FOL for corresponding problems.