PlanGPT-VL: Enhancing Urban Planning with Domain-Specific Vision-Language Models

In the field of urban planning, existing Vision-Language Models (VLMs) frequently fail to effectively analyze and evaluate planning maps, despite the critical importance of these visual elements for urban planners and related educational contexts. Planning maps, which visualize land use, infrastructure layouts, and functional zoning, require specialized understanding of spatial configurations, regulatory requirements, and multi-scale analysis. To address this challenge, we introduce PlanGPT-VL, the first domain-specific Vision-Language Model tailored specifically for urban planning maps. PlanGPT-VL employs three innovative approaches: (1) PlanAnno-V framework for high-quality VQA data synthesis, (2) Critical Point Thinking to reduce hallucinations through structured verification, and (3) comprehensive training methodology combining Supervised Fine-Tuning with frozen vision encoder parameters. Through systematic evaluation on our proposed PlanBench-V benchmark, we demonstrate that PlanGPT-VL significantly outperforms general-purpose state-of-the-art VLMs in specialized planning map interpretation tasks, offering urban planning professionals a reliable tool for map analysis, assessment, and educational applications while maintaining high factual accuracy. Our lightweight 7B parameter model achieves comparable performance to models exceeding 72B parameters, demonstrating efficient domain specialization without sacrificing performance.

Sparse Ellipsoidal Radial Basis Function Network for Point Cloud Surface Representation

Point cloud surface representation is a fundamental problem in computer graphics and vision. This paper presents a machine learning approach for approximating the signed distance function (SDF) of a point cloud using sparse ellipsoidal radial basis function networks, enabling a compact and accurate surface representation. Given the SDF values defined on the grid points constructed from the point cloud, our method approximates the SDF accurately with as few ellipsoidal radial basis functions (ERBFs) as possible, i.e., represent the SDF of a point cloud by sparse ERBFs. To balance sparsity and approximation precision, a dynamic multi-objective optimization strategy is introduced, which adaptively adds the regularization terms and jointly optimizes the weights, centers, shapes, and orientations of ERBFs. To improve computational efficiency, a nearest-neighbor-based data structure is employed, restricting function calculations to points near each Gaussian kernel center. The computations for each kernel are further parallelized on CUDA, which significantly improves the optimization speed. Additionally, a hierarchical octree-based refinement strategy is designed for training. Specifically, the initialization and optimization of network parameters are conducted using coarse grid points in the octree lattice structure. Subsequently, fine lattice points are progressively incorporated to accelerate model convergence and enhance training efficiency. Extensive experiments on multiple benchmark datasets demonstrate that our method outperforms previous sparse representation approaches in terms of accuracy, robustness, and computational efficiency. The corresponding code is publicly available at https://github.com/lianbobo/SE-RBFNet.git.

Solving multiscale elliptic problems by sparse radial basis function neural networks

Machine learning has been successfully applied to various fields of scientific computing in recent years. In this work, we propose a sparse radial basis function neural network method to solve elliptic partial differential equations (PDEs) with multiscale coefficients. Inspired by the deep mixed residual method, we rewrite the second-order problem into a first-order system and employ multiple radial basis function neural networks (RBFNNs) to approximate unknown functions in the system. To aviod the overfitting due to the simplicity of RBFNN, an additional regularization is introduced in the loss function. Thus the loss function contains two parts: the $L_2$ loss for the residual of the first-order system and boundary conditions, and the $\ell_1$ regularization term for the weights of radial basis functions (RBFs). An algorithm for optimizing the specific loss function is introduced to accelerate the training process. The accuracy and effectiveness of the proposed method are demonstrated through a collection of multiscale problems with scale separation, discontinuity and multiple scales from one to three dimensions. Notably, the $\ell_1$ regularization can achieve the goal of representing the solution by fewer RBFs. As a consequence, the total number of RBFs scales like $\mathcal{O}(\varepsilon^{-n\tau})$, where $\varepsilon$ is the smallest scale, $n$ is the dimensionality, and $\tau$ is typically smaller than $1$. It is worth mentioning that the proposed method not only has the numerical convergence and thus provides a reliable numerical solution in three dimensions when a classical method is typically not affordable, but also outperforms most other available machine learning methods in terms of accuracy and robustness.

Image Segmentation Based on Multiscale Fast Spectral Clustering

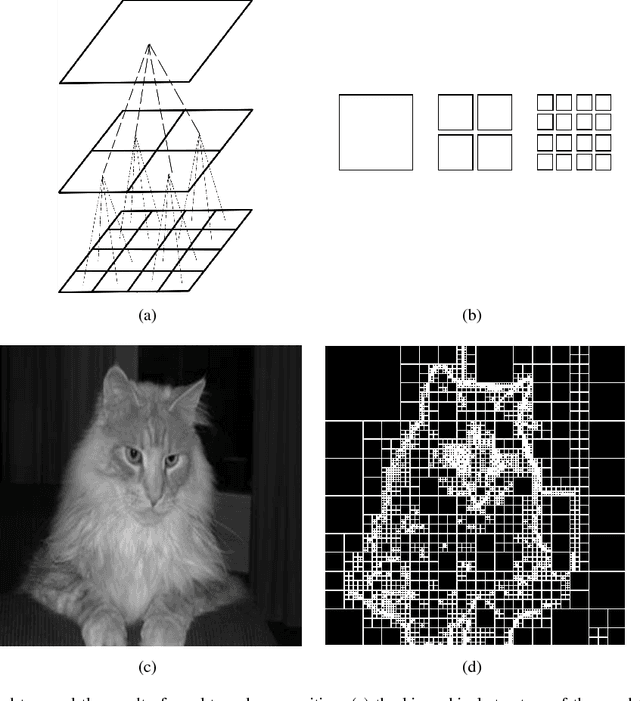
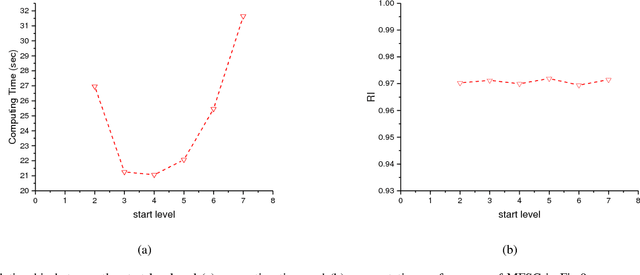
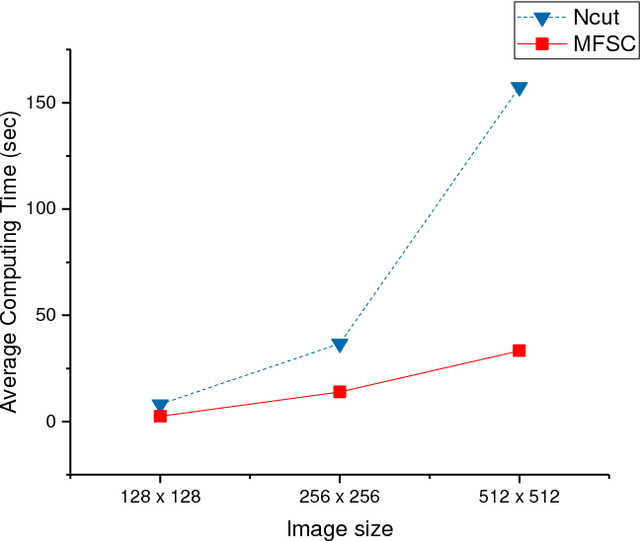
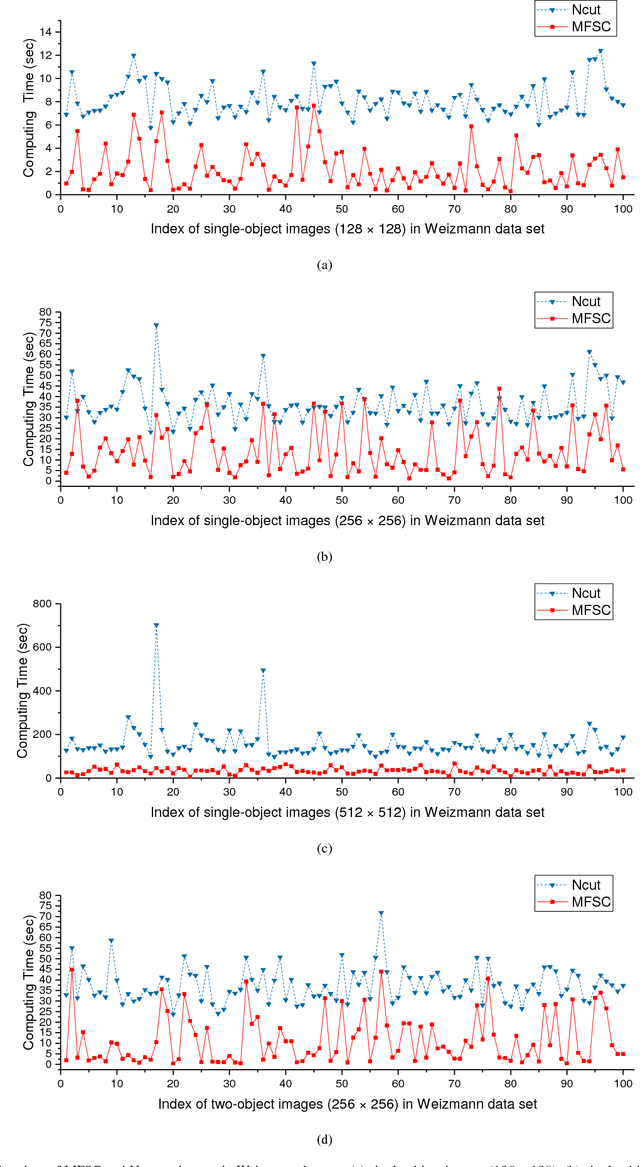
In recent years, spectral clustering has become one of the most popular clustering algorithms for image segmentation. However, it has restricted applicability to large-scale images due to its high computational complexity. In this paper, we first propose a novel algorithm called Fast Spectral Clustering based on quad-tree decomposition. The algorithm focuses on the spectral clustering at superpixel level and its computational complexity is O(nlogn) + O(m) + O(m^(3/2)); its memory cost is O(m), where n and m are the numbers of pixels and the superpixels of a image. Then we propose Multiscale Fast Spectral Clustering by improving Fast Spectral Clustering, which is based on the hierarchical structure of the quad-tree. The computational complexity of Multiscale Fast Spectral Clustering is O(nlogn) and its memory cost is O(m). Extensive experiments on real large-scale images demonstrate that Multiscale Fast Spectral Clustering outperforms Normalized cut in terms of lower computational complexity and memory cost, with comparable clustering accuracy.