Sparse Ellipsoidal Radial Basis Function Network for Point Cloud Surface Representation

Point cloud surface representation is a fundamental problem in computer graphics and vision. This paper presents a machine learning approach for approximating the signed distance function (SDF) of a point cloud using sparse ellipsoidal radial basis function networks, enabling a compact and accurate surface representation. Given the SDF values defined on the grid points constructed from the point cloud, our method approximates the SDF accurately with as few ellipsoidal radial basis functions (ERBFs) as possible, i.e., represent the SDF of a point cloud by sparse ERBFs. To balance sparsity and approximation precision, a dynamic multi-objective optimization strategy is introduced, which adaptively adds the regularization terms and jointly optimizes the weights, centers, shapes, and orientations of ERBFs. To improve computational efficiency, a nearest-neighbor-based data structure is employed, restricting function calculations to points near each Gaussian kernel center. The computations for each kernel are further parallelized on CUDA, which significantly improves the optimization speed. Additionally, a hierarchical octree-based refinement strategy is designed for training. Specifically, the initialization and optimization of network parameters are conducted using coarse grid points in the octree lattice structure. Subsequently, fine lattice points are progressively incorporated to accelerate model convergence and enhance training efficiency. Extensive experiments on multiple benchmark datasets demonstrate that our method outperforms previous sparse representation approaches in terms of accuracy, robustness, and computational efficiency. The corresponding code is publicly available at https://github.com/lianbobo/SE-RBFNet.git.

Image Segmentation Based on Multiscale Fast Spectral Clustering

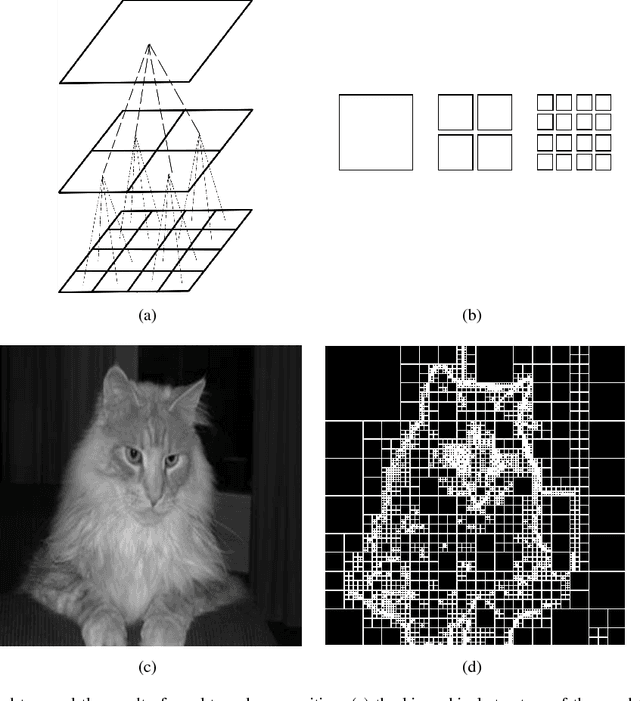
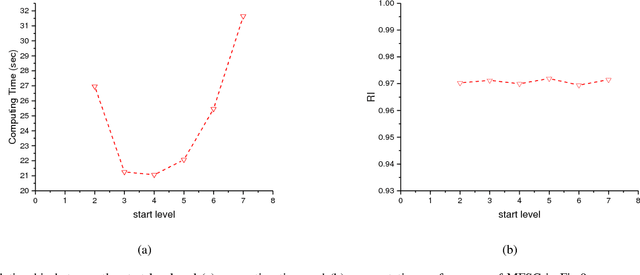
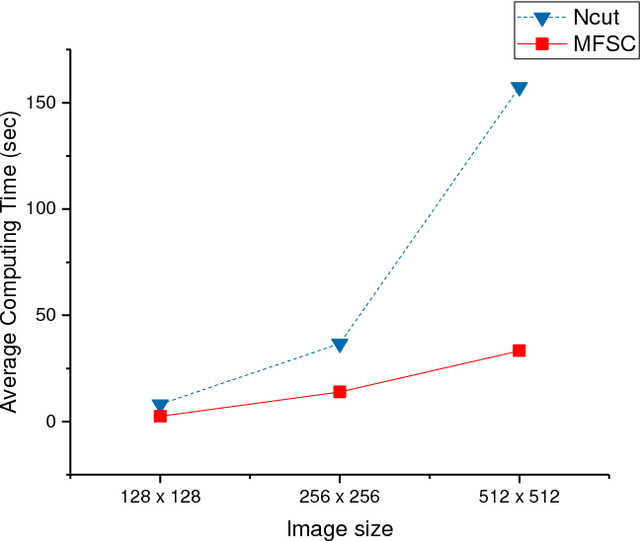
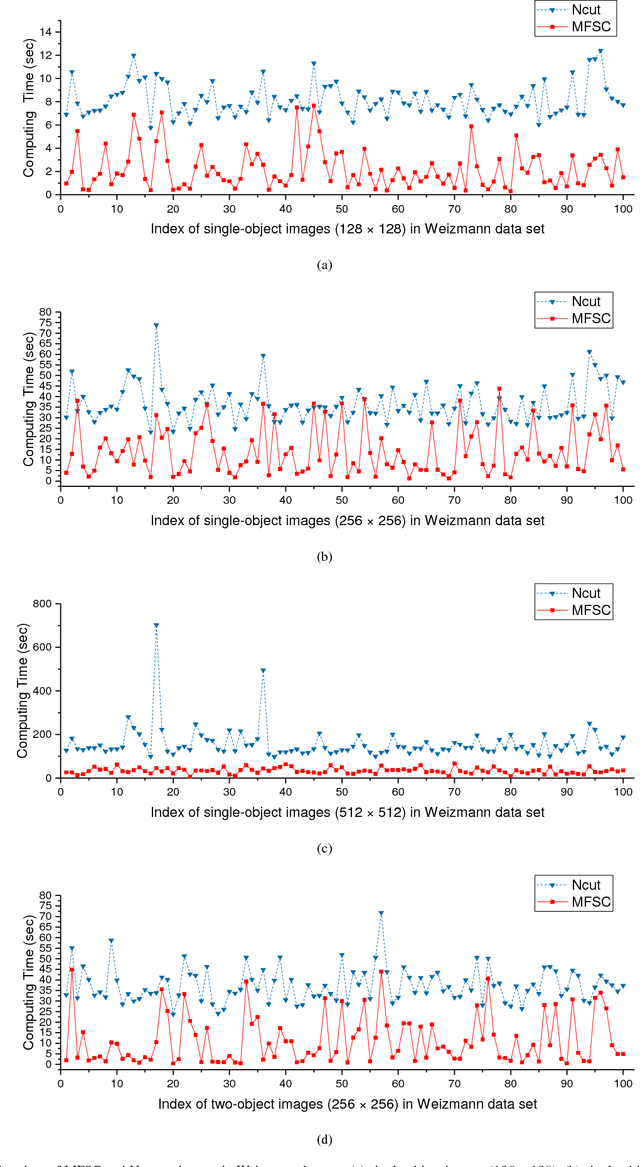
In recent years, spectral clustering has become one of the most popular clustering algorithms for image segmentation. However, it has restricted applicability to large-scale images due to its high computational complexity. In this paper, we first propose a novel algorithm called Fast Spectral Clustering based on quad-tree decomposition. The algorithm focuses on the spectral clustering at superpixel level and its computational complexity is O(nlogn) + O(m) + O(m^(3/2)); its memory cost is O(m), where n and m are the numbers of pixels and the superpixels of a image. Then we propose Multiscale Fast Spectral Clustering by improving Fast Spectral Clustering, which is based on the hierarchical structure of the quad-tree. The computational complexity of Multiscale Fast Spectral Clustering is O(nlogn) and its memory cost is O(m). Extensive experiments on real large-scale images demonstrate that Multiscale Fast Spectral Clustering outperforms Normalized cut in terms of lower computational complexity and memory cost, with comparable clustering accuracy.