KITINet: Kinetics Theory Inspired Network Architectures with PDE Simulation Approaches

Despite the widely recognized success of residual connections in modern neural networks, their design principles remain largely heuristic. This paper introduces KITINet (Kinetics Theory Inspired Network), a novel architecture that reinterprets feature propagation through the lens of non-equilibrium particle dynamics and partial differential equation (PDE) simulation. At its core, we propose a residual module that models feature updates as the stochastic evolution of a particle system, numerically simulated via a discretized solver for the Boltzmann transport equation (BTE). This formulation mimics particle collisions and energy exchange, enabling adaptive feature refinement via physics-informed interactions. Additionally, we reveal that this mechanism induces network parameter condensation during training, where parameters progressively concentrate into a sparse subset of dominant channels. Experiments on scientific computation (PDE operator), image classification (CIFAR-10/100), and text classification (IMDb/SNLI) show consistent improvements over classic network baselines, with negligible increase of FLOPs.

KO: Kinetics-inspired Neural Optimizer with PDE Simulation Approaches

The design of optimization algorithms for neural networks remains a critical challenge, with most existing methods relying on heuristic adaptations of gradient-based approaches. This paper introduces KO (Kinetics-inspired Optimizer), a novel neural optimizer inspired by kinetic theory and partial differential equation (PDE) simulations. We reimagine the training dynamics of network parameters as the evolution of a particle system governed by kinetic principles, where parameter updates are simulated via a numerical scheme for the Boltzmann transport equation (BTE) that models stochastic particle collisions. This physics-driven approach inherently promotes parameter diversity during optimization, mitigating the phenomenon of parameter condensation, i.e. collapse of network parameters into low-dimensional subspaces, through mechanisms analogous to thermal diffusion in physical systems. We analyze this property, establishing both a mathematical proof and a physical interpretation. Extensive experiments on image classification (CIFAR-10/100, ImageNet) and text classification (IMDB, Snips) tasks demonstrate that KO consistently outperforms baseline optimizers (e.g., Adam, SGD), achieving accuracy improvements while computation cost remains comparable.

Optimal Control Operator Perspective and a Neural Adaptive Spectral Method

Optimal control problems (OCPs) involve finding a control function for a dynamical system such that a cost functional is optimized. It is central to physical systems in both academia and industry. In this paper, we propose a novel instance-solution control operator perspective, which solves OCPs in a one-shot manner without direct dependence on the explicit expression of dynamics or iterative optimization processes. The control operator is implemented by a new neural operator architecture named Neural Adaptive Spectral Method (NASM), a generalization of classical spectral methods. We theoretically validate the perspective and architecture by presenting the approximation error bounds of NASM for the control operator. Experiments on synthetic environments and a real-world dataset verify the effectiveness and efficiency of our approach, including substantial speedup in running time, and high-quality in- and out-of-distribution generalization.

Learning Neural Hamiltonian Dynamics: A Methodological Overview

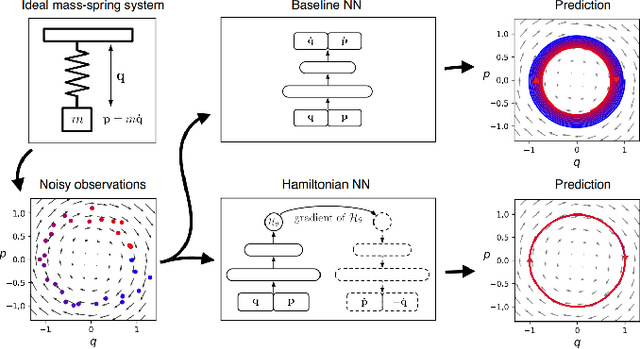
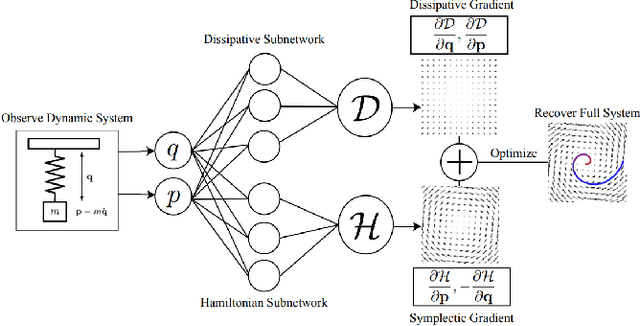
The past few years have witnessed an increased interest in learning Hamiltonian dynamics in deep learning frameworks. As an inductive bias based on physical laws, Hamiltonian dynamics endow neural networks with accurate long-term prediction, interpretability, and data-efficient learning. However, Hamiltonian dynamics also bring energy conservation or dissipation assumptions on the input data and additional computational overhead. In this paper, we systematically survey recently proposed Hamiltonian neural network models, with a special emphasis on methodologies. In general, we discuss the major contributions of these models, and compare them in four overlapping directions: 1) generalized Hamiltonian system; 2) symplectic integration, 3) generalized input form, and 4) extended problem settings. We also provide an outlook of the fundamental challenges and emerging opportunities in this area.

Perception Improvement for Free: Exploring Imperceptible Black-box Adversarial Attacks on Image Classification

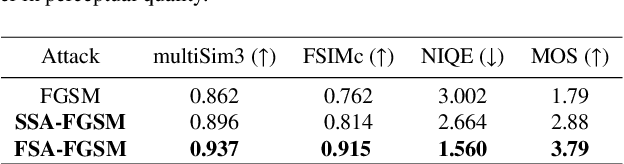
Deep neural networks are vulnerable to adversarial attacks. White-box adversarial attacks can fool neural networks with small adversarial perturbations, especially for large size images. However, keeping successful adversarial perturbations imperceptible is especially challenging for transfer-based black-box adversarial attacks. Often such adversarial examples can be easily spotted due to their unpleasantly poor visual qualities, which compromises the threat of adversarial attacks in practice. In this study, to improve the image quality of black-box adversarial examples perceptually, we propose structure-aware adversarial attacks by generating adversarial images based on psychological perceptual models. Specifically, we allow higher perturbations on perceptually insignificant regions, while assigning lower or no perturbation on visually sensitive regions. In addition to the proposed spatial-constrained adversarial perturbations, we also propose a novel structure-aware frequency adversarial attack method in the discrete cosine transform (DCT) domain. Since the proposed attacks are independent of the gradient estimation, they can be directly incorporated with existing gradient-based attacks. Experimental results show that, with the comparable attack success rate (ASR), the proposed methods can produce adversarial examples with considerably improved visual quality for free. With the comparable perceptual quality, the proposed approaches achieve higher attack success rates: particularly for the frequency structure-aware attacks, the average ASR improves more than 10% over the baseline attacks.