KITINet: Kinetics Theory Inspired Network Architectures with PDE Simulation Approaches

Despite the widely recognized success of residual connections in modern neural networks, their design principles remain largely heuristic. This paper introduces KITINet (Kinetics Theory Inspired Network), a novel architecture that reinterprets feature propagation through the lens of non-equilibrium particle dynamics and partial differential equation (PDE) simulation. At its core, we propose a residual module that models feature updates as the stochastic evolution of a particle system, numerically simulated via a discretized solver for the Boltzmann transport equation (BTE). This formulation mimics particle collisions and energy exchange, enabling adaptive feature refinement via physics-informed interactions. Additionally, we reveal that this mechanism induces network parameter condensation during training, where parameters progressively concentrate into a sparse subset of dominant channels. Experiments on scientific computation (PDE operator), image classification (CIFAR-10/100), and text classification (IMDb/SNLI) show consistent improvements over classic network baselines, with negligible increase of FLOPs.

KO: Kinetics-inspired Neural Optimizer with PDE Simulation Approaches

The design of optimization algorithms for neural networks remains a critical challenge, with most existing methods relying on heuristic adaptations of gradient-based approaches. This paper introduces KO (Kinetics-inspired Optimizer), a novel neural optimizer inspired by kinetic theory and partial differential equation (PDE) simulations. We reimagine the training dynamics of network parameters as the evolution of a particle system governed by kinetic principles, where parameter updates are simulated via a numerical scheme for the Boltzmann transport equation (BTE) that models stochastic particle collisions. This physics-driven approach inherently promotes parameter diversity during optimization, mitigating the phenomenon of parameter condensation, i.e. collapse of network parameters into low-dimensional subspaces, through mechanisms analogous to thermal diffusion in physical systems. We analyze this property, establishing both a mathematical proof and a physical interpretation. Extensive experiments on image classification (CIFAR-10/100, ImageNet) and text classification (IMDB, Snips) tasks demonstrate that KO consistently outperforms baseline optimizers (e.g., Adam, SGD), achieving accuracy improvements while computation cost remains comparable.

Low Rank Representation on Riemannian Manifold of Square Root Densities

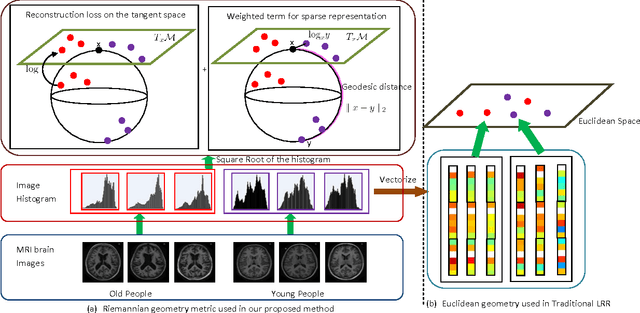
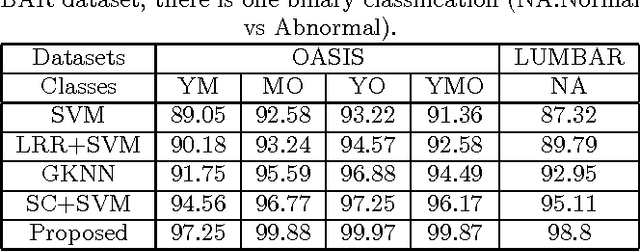
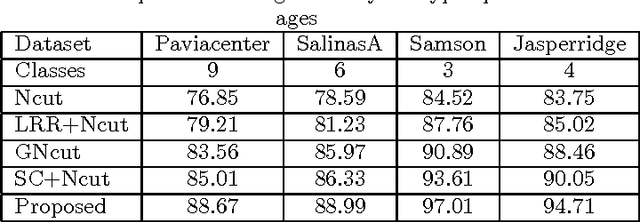
In this paper, we present a novel low rank representation (LRR) algorithm for data lying on the manifold of square root densities. Unlike traditional LRR methods which rely on the assumption that the data points are vectors in the Euclidean space, our new algorithm is designed to incorporate the intrinsic geometric structure and geodesic distance of the manifold. Experiments on several computer vision datasets showcase its noise robustness and superior performance on classification and subspace clustering compared to other state-of-the-art approaches.