UGM2N: An Unsupervised and Generalizable Mesh Movement Network via M-Uniform Loss

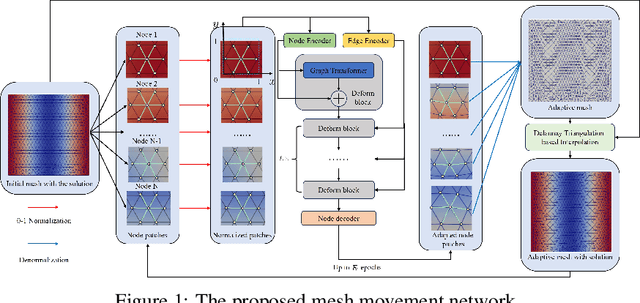
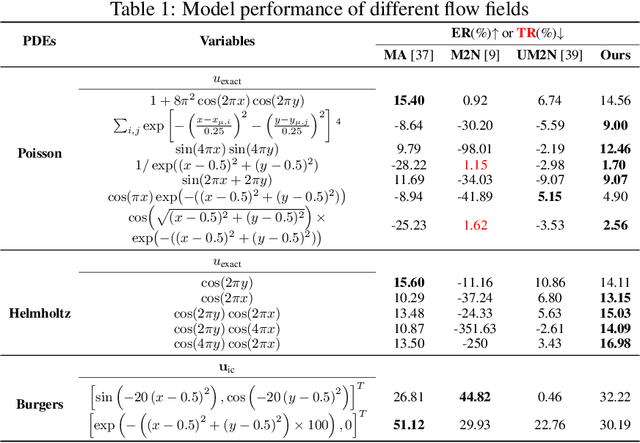
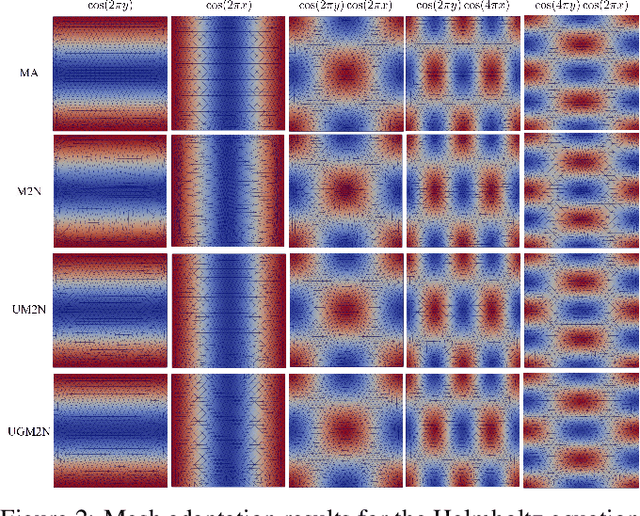
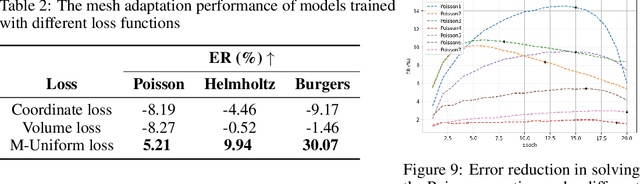
Partial differential equations (PDEs) form the mathematical foundation for modeling physical systems in science and engineering, where numerical solutions demand rigorous accuracy-efficiency tradeoffs. Mesh movement techniques address this challenge by dynamically relocating mesh nodes to rapidly-varying regions, enhancing both simulation accuracy and computational efficiency. However, traditional approaches suffer from high computational complexity and geometric inflexibility, limiting their applicability, and existing supervised learning-based approaches face challenges in zero-shot generalization across diverse PDEs and mesh topologies.In this paper, we present an Unsupervised and Generalizable Mesh Movement Network (UGM2N). We first introduce unsupervised mesh adaptation through localized geometric feature learning, eliminating the dependency on pre-adapted meshes. We then develop a physics-constrained loss function, M-Uniform loss, that enforces mesh equidistribution at the nodal level.Experimental results demonstrate that the proposed network exhibits equation-agnostic generalization and geometric independence in efficient mesh adaptation. It demonstrates consistent superiority over existing methods, including robust performance across diverse PDEs and mesh geometries, scalability to multi-scale resolutions and guaranteed error reduction without mesh tangling.

State-space Decomposition Model for Video Prediction Considering Long-term Motion Trend

Stochastic video prediction enables the consideration of uncertainty in future motion, thereby providing a better reflection of the dynamic nature of the environment. Stochastic video prediction methods based on image auto-regressive recurrent models need to feed their predictions back into the latent space. Conversely, the state-space models, which decouple frame synthesis and temporal prediction, proves to be more efficient. However, inferring long-term temporal information about motion and generalizing to dynamic scenarios under non-stationary assumptions remains an unresolved challenge. In this paper, we propose a state-space decomposition stochastic video prediction model that decomposes the overall video frame generation into deterministic appearance prediction and stochastic motion prediction. Through adaptive decomposition, the model's generalization capability to dynamic scenarios is enhanced. In the context of motion prediction, obtaining a prior on the long-term trend of future motion is crucial. Thus, in the stochastic motion prediction branch, we infer the long-term motion trend from conditional frames to guide the generation of future frames that exhibit high consistency with the conditional frames. Experimental results demonstrate that our model outperforms baselines on multiple datasets.