UGM2N: An Unsupervised and Generalizable Mesh Movement Network via M-Uniform Loss

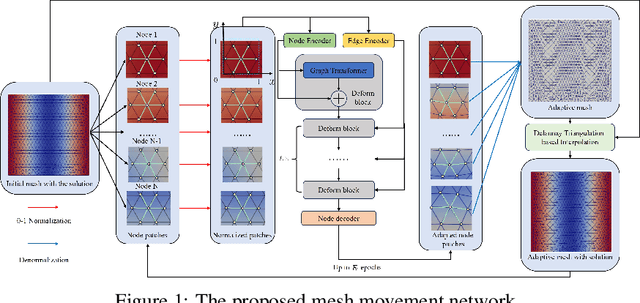
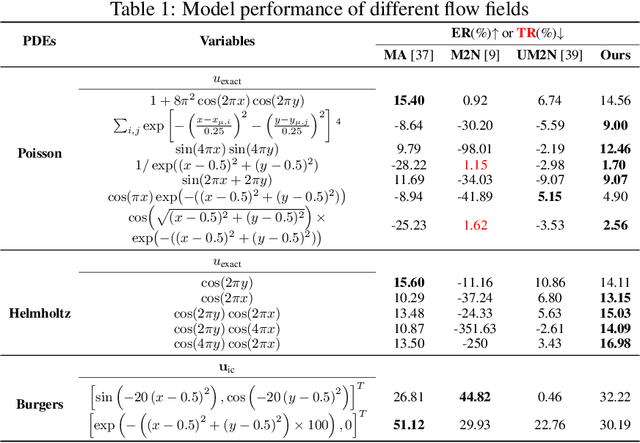
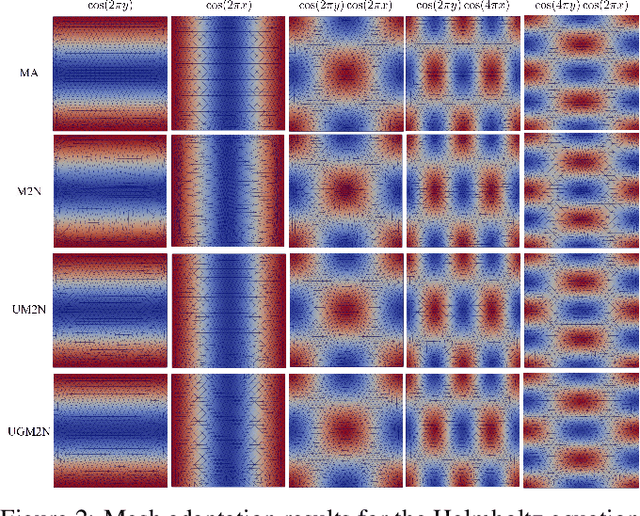
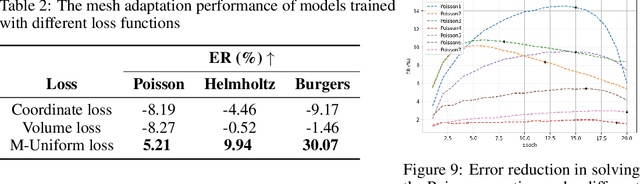
Partial differential equations (PDEs) form the mathematical foundation for modeling physical systems in science and engineering, where numerical solutions demand rigorous accuracy-efficiency tradeoffs. Mesh movement techniques address this challenge by dynamically relocating mesh nodes to rapidly-varying regions, enhancing both simulation accuracy and computational efficiency. However, traditional approaches suffer from high computational complexity and geometric inflexibility, limiting their applicability, and existing supervised learning-based approaches face challenges in zero-shot generalization across diverse PDEs and mesh topologies.In this paper, we present an Unsupervised and Generalizable Mesh Movement Network (UGM2N). We first introduce unsupervised mesh adaptation through localized geometric feature learning, eliminating the dependency on pre-adapted meshes. We then develop a physics-constrained loss function, M-Uniform loss, that enforces mesh equidistribution at the nodal level.Experimental results demonstrate that the proposed network exhibits equation-agnostic generalization and geometric independence in efficient mesh adaptation. It demonstrates consistent superiority over existing methods, including robust performance across diverse PDEs and mesh geometries, scalability to multi-scale resolutions and guaranteed error reduction without mesh tangling.