Hyperbolic Graph Neural Networks

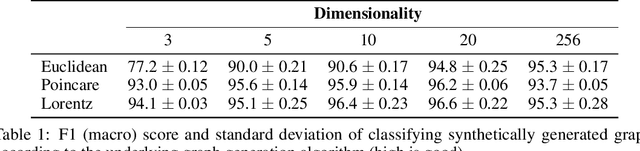
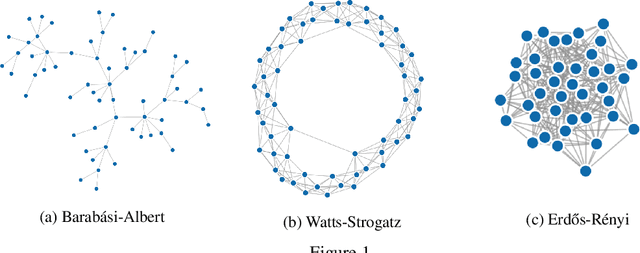
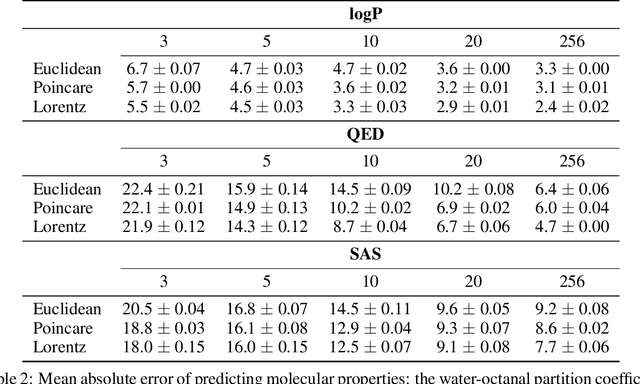
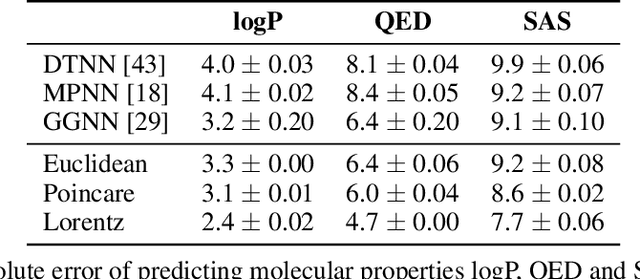
Learning from graph-structured data is an important task in machine learning and artificial intelligence, for which Graph Neural Networks (GNNs) have shown great promise. Motivated by recent advances in geometric representation learning, we propose a novel GNN architecture for learning representations on Riemannian manifolds with differentiable exponential and logarithmic maps. We develop a scalable algorithm for modeling the structural properties of graphs, comparing Euclidean and hyperbolic geometry. In our experiments, we show that hyperbolic GNNs can lead to substantial improvements on various benchmark datasets.

Task-Driven Modular Networks for Zero-Shot Compositional Learning

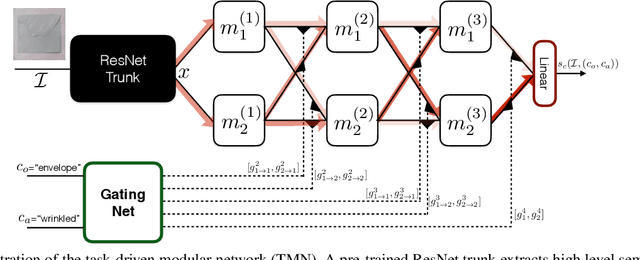
One of the hallmarks of human intelligence is the ability to compose learned knowledge into novel concepts which can be recognized without a single training example. In contrast, current state-of-the-art methods require hundreds of training examples for each possible category to build reliable and accurate classifiers. To alleviate this striking difference in efficiency, we propose a task-driven modular architecture for compositional reasoning and sample efficient learning. Our architecture consists of a set of neural network modules, which are small fully connected layers operating in semantic concept space. These modules are configured through a gating function conditioned on the task to produce features representing the compatibility between the input image and the concept under consideration. This enables us to express tasks as a combination of sub-tasks and to generalize to unseen categories by reweighting a set of small modules. Furthermore, the network can be trained efficiently as it is fully differentiable and its modules operate on small sub-spaces. We focus our study on the problem of compositional zero-shot classification of object-attribute categories. We show in our experiments that current evaluation metrics are flawed as they only consider unseen object-attribute pairs. When extending the evaluation to the generalized setting which accounts also for pairs seen during training, we discover that naive baseline methods perform similarly or better than current approaches. However, our modular network is able to outperform all existing approaches on two widely-used benchmark datasets.

Inferring Concept Hierarchies from Text Corpora via Hyperbolic Embeddings

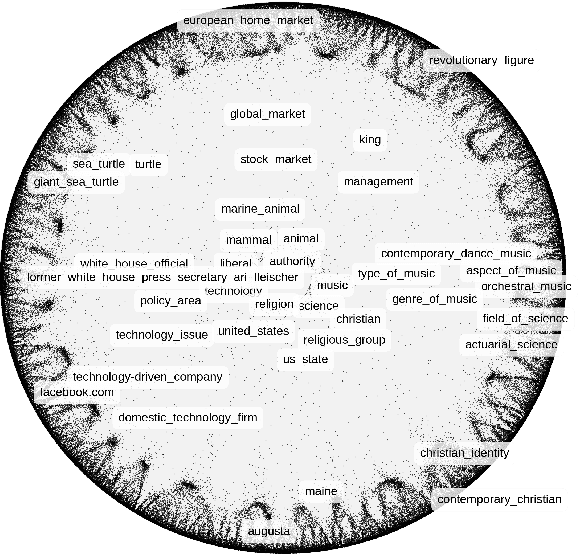
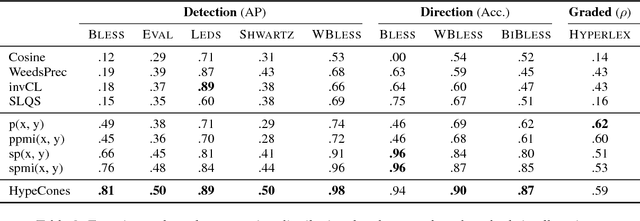
We consider the task of inferring is-a relationships from large text corpora. For this purpose, we propose a new method combining hyperbolic embeddings and Hearst patterns. This approach allows us to set appropriate constraints for inferring concept hierarchies from distributional contexts while also being able to predict missing is-a relationships and to correct wrong extractions. Moreover -- and in contrast with other methods -- the hierarchical nature of hyperbolic space allows us to learn highly efficient representations and to improve the taxonomic consistency of the inferred hierarchies. Experimentally, we show that our approach achieves state-of-the-art performance on several commonly-used benchmarks.

Learning Continuous Hierarchies in the Lorentz Model of Hyperbolic Geometry

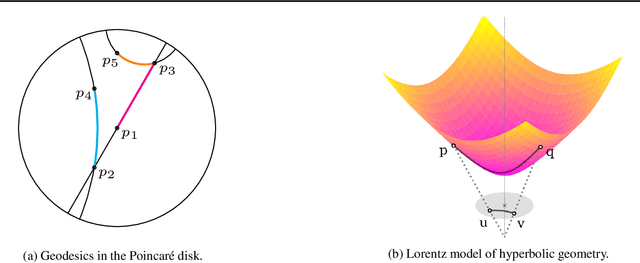
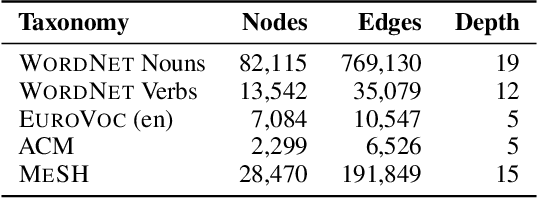
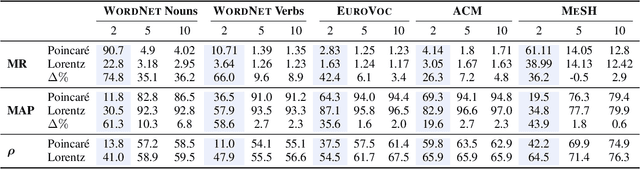
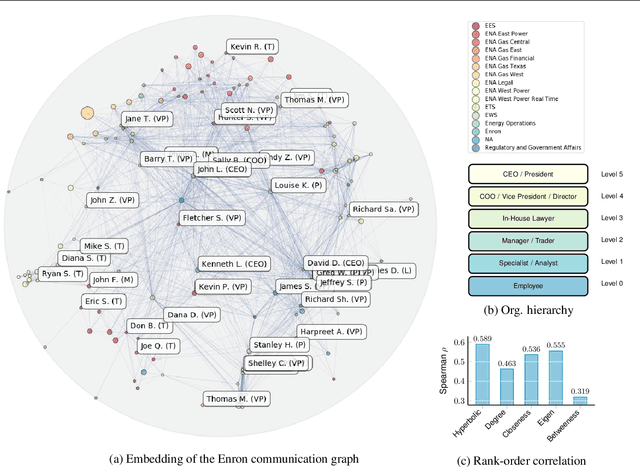
We are concerned with the discovery of hierarchical relationships from large-scale unstructured similarity scores. For this purpose, we study different models of hyperbolic space and find that learning embeddings in the Lorentz model is substantially more efficient than in the Poincar\'e-ball model. We show that the proposed approach allows us to learn high-quality embeddings of large taxonomies which yield improvements over Poincar\'e embeddings, especially in low dimensions. Lastly, we apply our model to discover hierarchies in two real-world datasets: we show that an embedding in hyperbolic space can reveal important aspects of a company's organizational structure as well as reveal historical relationships between language families.

Hearst Patterns Revisited: Automatic Hypernym Detection from Large Text Corpora

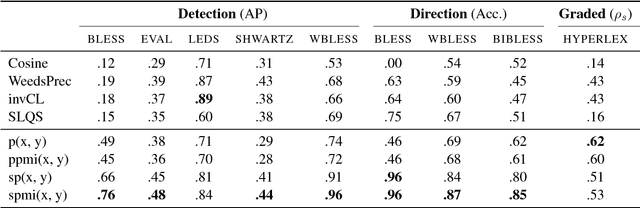
Methods for unsupervised hypernym detection may broadly be categorized according to two paradigms: pattern-based and distributional methods. In this paper, we study the performance of both approaches on several hypernymy tasks and find that simple pattern-based methods consistently outperform distributional methods on common benchmark datasets. Our results show that pattern-based models provide important contextual constraints which are not yet captured in distributional methods.

Learning Visually Grounded Sentence Representations

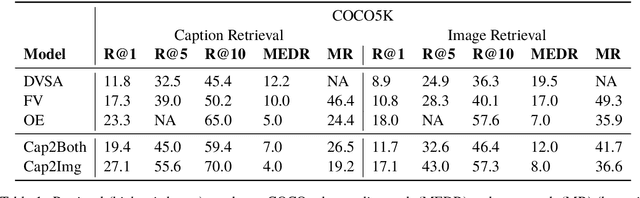
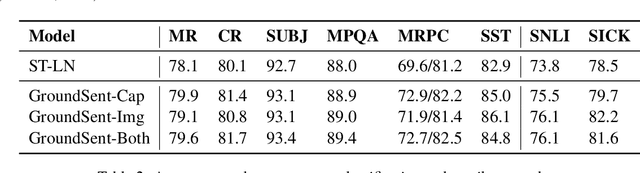
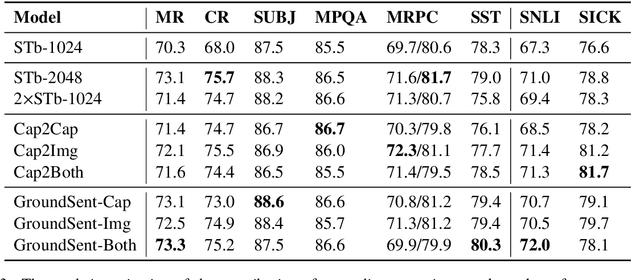
We introduce a variety of models, trained on a supervised image captioning corpus to predict the image features for a given caption, to perform sentence representation grounding. We train a grounded sentence encoder that achieves good performance on COCO caption and image retrieval and subsequently show that this encoder can successfully be transferred to various NLP tasks, with improved performance over text-only models. Lastly, we analyze the contribution of grounding, and show that word embeddings learned by this system outperform non-grounded ones.

Separating Self-Expression and Visual Content in Hashtag Supervision

The variety, abundance, and structured nature of hashtags make them an interesting data source for training vision models. For instance, hashtags have the potential to significantly reduce the problem of manual supervision and annotation when learning vision models for a large number of concepts. However, a key challenge when learning from hashtags is that they are inherently subjective because they are provided by users as a form of self-expression. As a consequence, hashtags may have synonyms (different hashtags referring to the same visual content) and may be ambiguous (the same hashtag referring to different visual content). These challenges limit the effectiveness of approaches that simply treat hashtags as image-label pairs. This paper presents an approach that extends upon modeling simple image-label pairs by modeling the joint distribution of images, hashtags, and users. We demonstrate the efficacy of such approaches in image tagging and retrieval experiments, and show how the joint model can be used to perform user-conditional retrieval and tagging.

Fast Linear Model for Knowledge Graph Embeddings

This paper shows that a simple baseline based on a Bag-of-Words (BoW) representation learns surprisingly good knowledge graph embeddings. By casting knowledge base completion and question answering as supervised classification problems, we observe that modeling co-occurences of entities and relations leads to state-of-the-art performance with a training time of a few minutes using the open sourced library fastText.

Complex and Holographic Embeddings of Knowledge Graphs: A Comparison

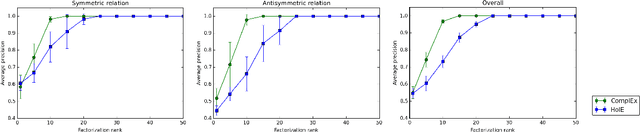
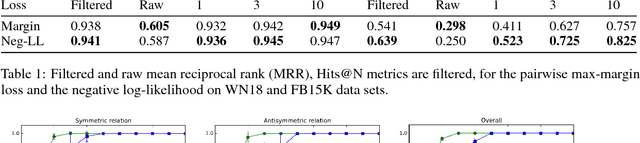
Embeddings of knowledge graphs have received significant attention due to their excellent performance for tasks like link prediction and entity resolution. In this short paper, we are providing a comparison of two state-of-the-art knowledge graph embeddings for which their equivalence has recently been established, i.e., ComplEx and HolE [Nickel, Rosasco, and Poggio, 2016; Trouillon et al., 2016; Hayashi and Shimbo, 2017]. First, we briefly review both models and discuss how their scoring functions are equivalent. We then analyze the discrepancy of results reported in the original articles, and show experimentally that they are likely due to the use of different loss functions. In further experiments, we evaluate the ability of both models to embed symmetric and antisymmetric patterns. Finally, we discuss advantages and disadvantages of both models and under which conditions one would be preferable to the other.

Poincaré Embeddings for Learning Hierarchical Representations

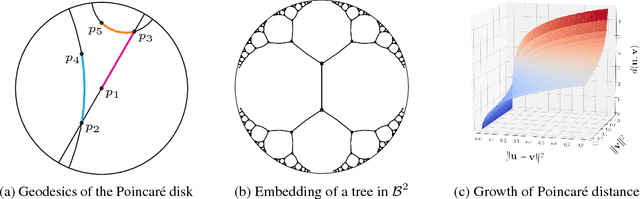
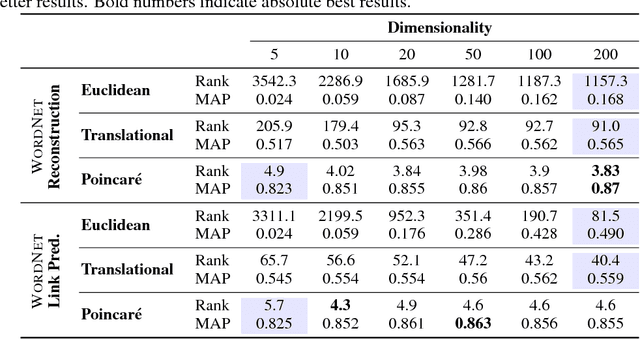
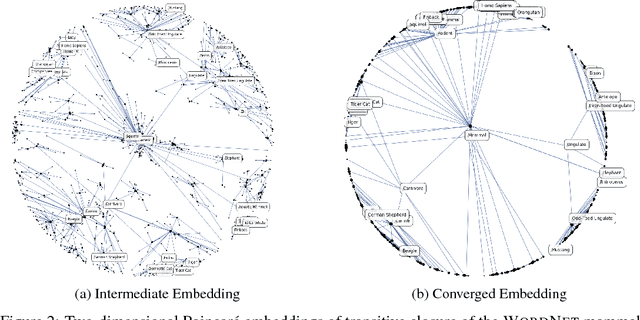
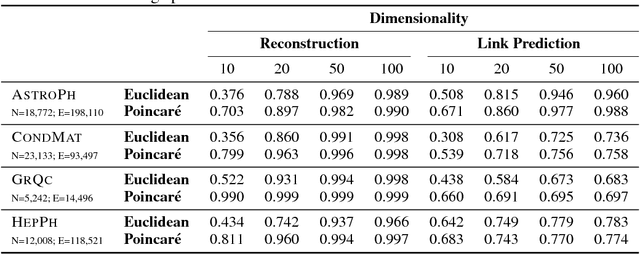
Representation learning has become an invaluable approach for learning from symbolic data such as text and graphs. However, while complex symbolic datasets often exhibit a latent hierarchical structure, state-of-the-art methods typically learn embeddings in Euclidean vector spaces, which do not account for this property. For this purpose, we introduce a new approach for learning hierarchical representations of symbolic data by embedding them into hyperbolic space -- or more precisely into an n-dimensional Poincar\'e ball. Due to the underlying hyperbolic geometry, this allows us to learn parsimonious representations of symbolic data by simultaneously capturing hierarchy and similarity. We introduce an efficient algorithm to learn the embeddings based on Riemannian optimization and show experimentally that Poincar\'e embeddings outperform Euclidean embeddings significantly on data with latent hierarchies, both in terms of representation capacity and in terms of generalization ability.