Collaborating Action by Action: A Multi-agent LLM Framework for Embodied Reasoning

Collaboration is ubiquitous and essential in day-to-day life -- from exchanging ideas, to delegating tasks, to generating plans together. This work studies how LLMs can adaptively collaborate to perform complex embodied reasoning tasks. To this end we introduce MINDcraft, an easily extensible platform built to enable LLM agents to control characters in the open-world game of Minecraft; and MineCollab, a benchmark to test the different dimensions of embodied and collaborative reasoning. An experimental study finds that the primary bottleneck in collaborating effectively for current state-of-the-art agents is efficient natural language communication, with agent performance dropping as much as 15% when they are required to communicate detailed task completion plans. We conclude that existing LLM agents are ill-optimized for multi-agent collaboration, especially in embodied scenarios, and highlight the need to employ methods beyond in-context and imitation learning. Our website can be found here: https://mindcraft-minecollab.github.io/

A digital score of tumour-associated stroma infiltrating lymphocytes predicts survival in head and neck squamous cell carcinoma

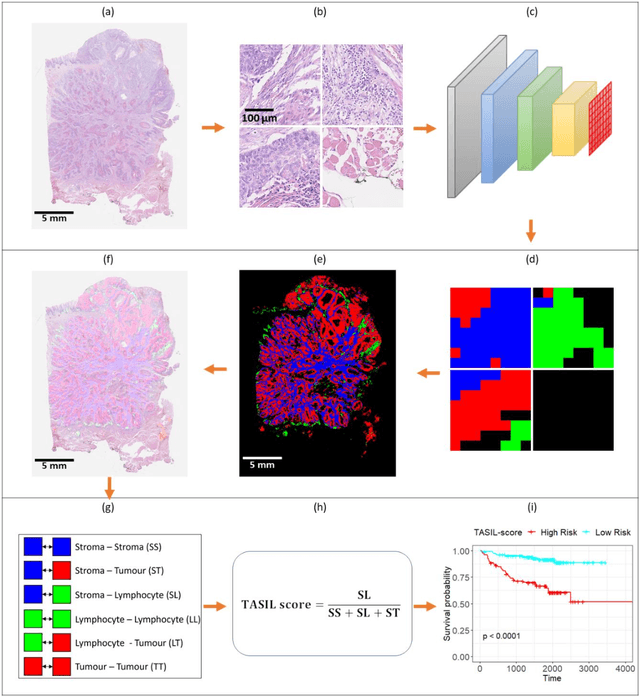
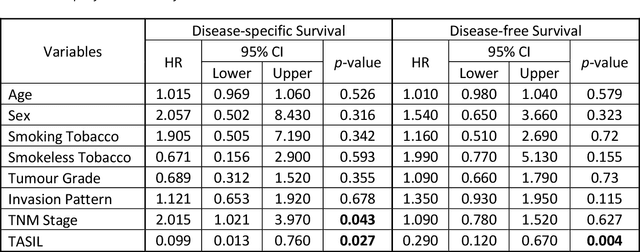
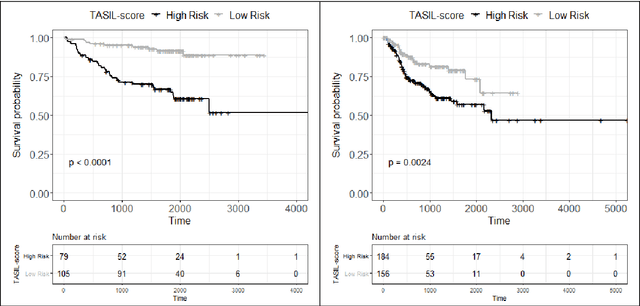
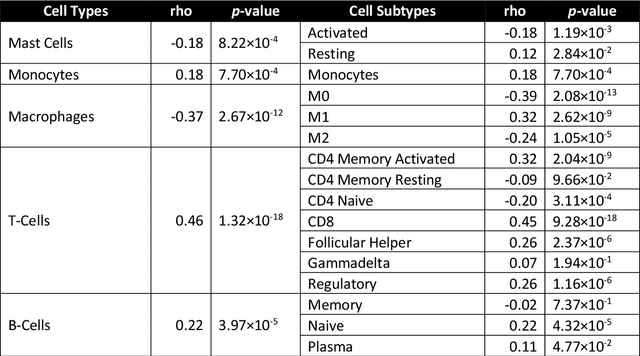
The infiltration of T-lymphocytes in the stroma and tumour is an indication of an effective immune response against the tumour, resulting in better survival. In this study, our aim is to explore the prognostic significance of tumour-associated stroma infiltrating lymphocytes (TASILs) in head and neck squamous cell carcinoma (HNSCC) through an AI based automated method. A deep learning based automated method was employed to segment tumour, stroma and lymphocytes in digitally scanned whole slide images of HNSCC tissue slides. The spatial patterns of lymphocytes and tumour-associated stroma were digitally quantified to compute the TASIL-score. Finally, prognostic significance of the TASIL-score for disease-specific and disease-free survival was investigated with the Cox proportional hazard analysis. Three different cohorts of Haematoxylin & Eosin (H&E) stained tissue slides of HNSCC cases (n=537 in total) were studied, including publicly available TCGA head and neck cancer cases. The TASIL-score carries prognostic significance (p=0.002) for disease-specific survival of HNSCC patients. The TASIL-score also shows a better separation between low- and high-risk patients as compared to the manual TIL scoring by pathologists for both disease-specific and disease-free survival. A positive correlation of TASIL-score with molecular estimates of CD8+ T cells was also found, which is in line with existing findings. To the best of our knowledge, this is the first study to automate the quantification of TASIL from routine H&E slides of head and neck cancer. Our TASIL-score based findings are aligned with the clinical knowledge with the added advantages of objectivity, reproducibility and strong prognostic value. A comprehensive evaluation on large multicentric cohorts is required before the proposed digital score can be adopted in clinical practice.

Projective Decomposition and Matrix Equivalence up to Scale

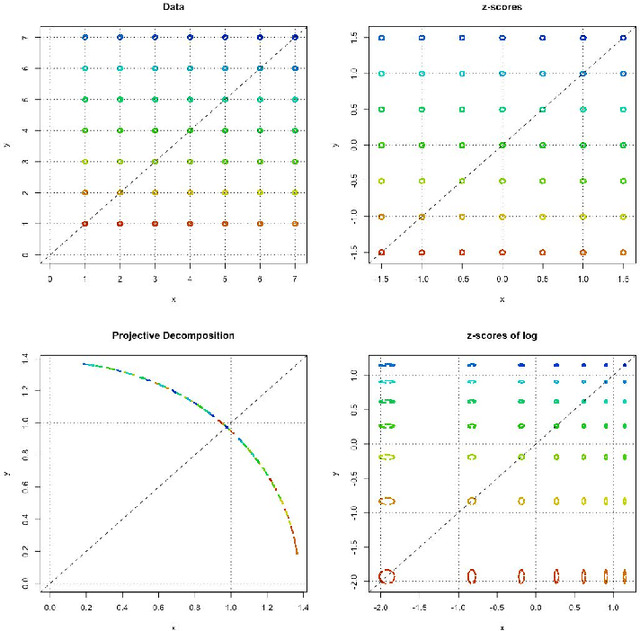
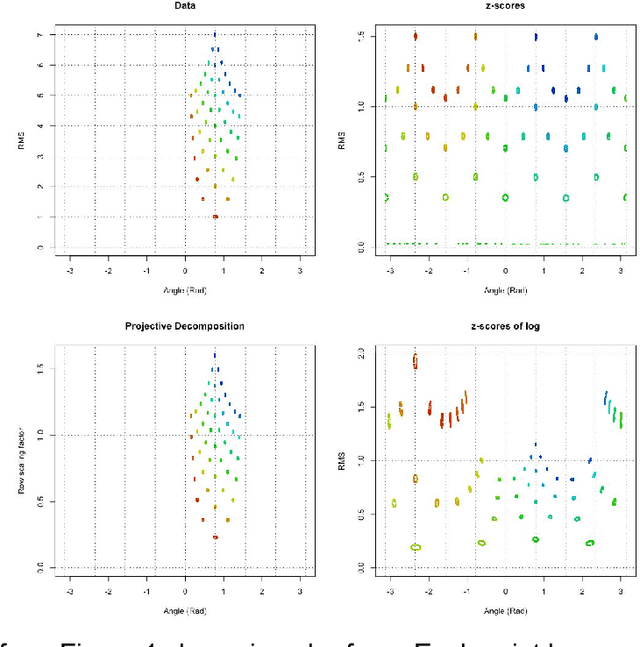
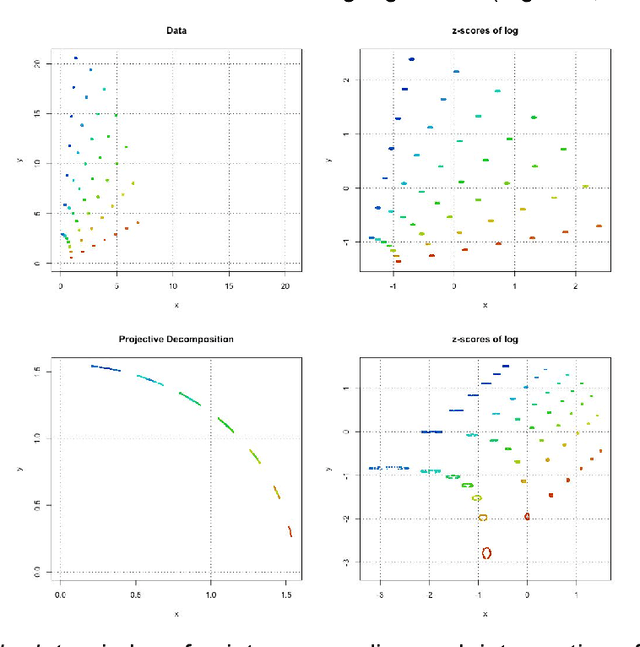
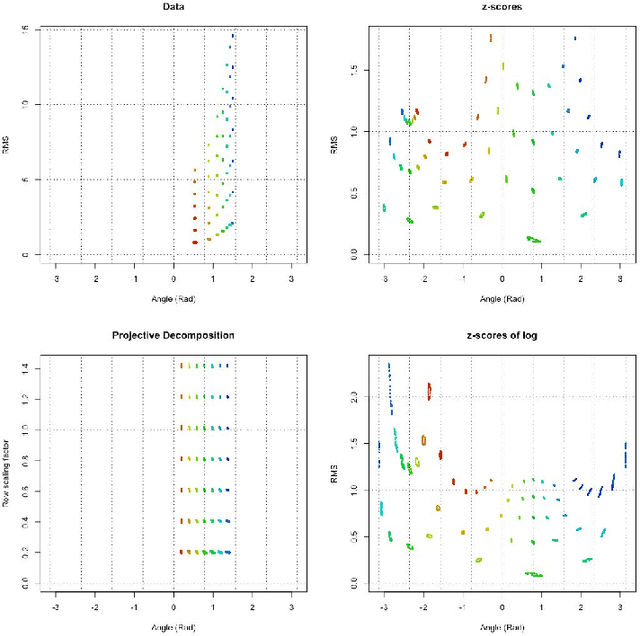
A data matrix may be seen simply as a means of organizing observations into rows ( e.g., by measured object) and into columns ( e.g., by measured variable) so that the observations can be analyzed with mathematical tools. As a mathematical object, a matrix defines a linear mapping between points representing weighted combinations of its rows (the row vector space) and points representing weighted combinations of its columns (the column vector space). From this perspective, a data matrix defines a relationship between the information that labels its rows and the information that labels its columns, and numerical methods are used to analyze this relationship. A first step is to normalize the data, transforming each observation from scales convenient for measurement to a common scale, on which addition and multiplication can meaningfully combine the different observations. For example, z-transformation rescales every variable to the same scale, standardized variation from an expected value, but ignores scale differences between measured objects. Here we develop the concepts and properties of projective decomposition, which applies the same normalization strategy to both rows and columns by separating the matrix into row- and column-scaling factors and a scale-normalized matrix. We show that different scalings of the same scale-normalized matrix form an equivalence class, and call the scale-normalized, canonical member of the class its scale-invariant form that preserves all pairwise relative ratios. Projective decomposition therefore provides a means of normalizing the broad class of ratio-scale data, in which relative ratios are of primary interest, onto a common scale without altering the ratios of interest, and simultaneously accounting for scale effects for both organizations of the matrix values. Both of these properties distinguish it from z-transformation.