Spectral-Spatial Diffusion Geometry for Hyperspectral Image Clustering

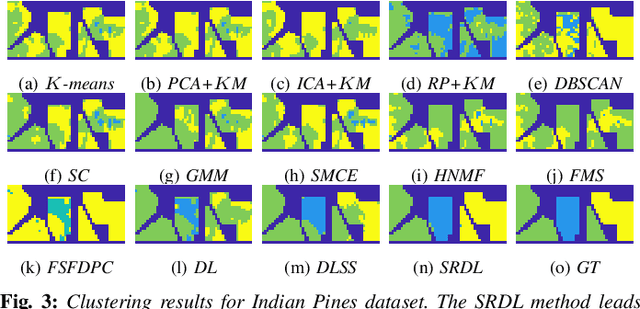
An unsupervised learning algorithm to cluster hyperspectral image (HSI) data is proposed that exploits spatially-regularized random walks. Markov diffusions are defined on the space of HSI spectra with transitions constrained to near spatial neighbors. The explicit incorporation of spatial regularity into the diffusion construction leads to smoother random processes that are more adapted for unsupervised machine learning than those based on spectra alone. The regularized diffusion process is subsequently used to embed the high-dimensional HSI into a lower dimensional space through diffusion distances. Cluster modes are computed using density estimation and diffusion distances, and all other points are labeled according to these modes. The proposed method has low computational complexity and performs competitively against state-of-the-art HSI clustering algorithms on real data. In particular, the proposed spatial regularization confers an empirical advantage over non-regularized methods.

Nonparametric inference of interaction laws in systems of agents from trajectory data

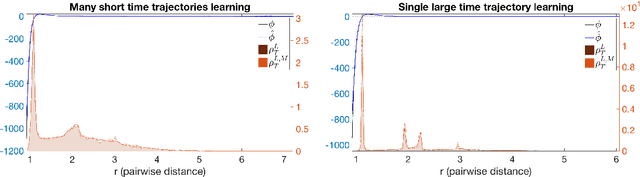
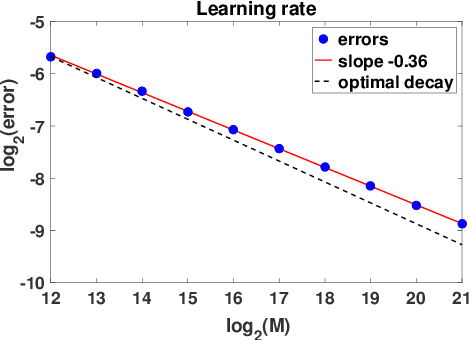
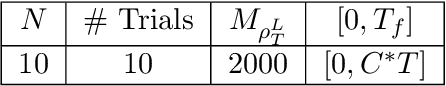
Inferring the laws of interaction between particles and agents in complex dynamical systems from observational data is a fundamental challenge in a wide variety of disciplines. We propose a non-parametric statistical learning approach to estimate the governing laws of distance-based interactions, with no reference or assumption about their analytical form, from data consisting trajectories of interacting agents. We demonstrate the effectiveness of our learning approach both by providing theoretical guarantees, and by testing the approach on a variety of prototypical systems in various disciplines. These systems include homogeneous and heterogeneous agents systems, ranging from particle systems in fundamental physics to agent-based systems modeling opinion dynamics under the social influence, prey-predator dynamics, flocking and swarming, and phototaxis in cell dynamics.

Unsupervised Clustering and Active Learning of Hyperspectral Images with Nonlinear Diffusion

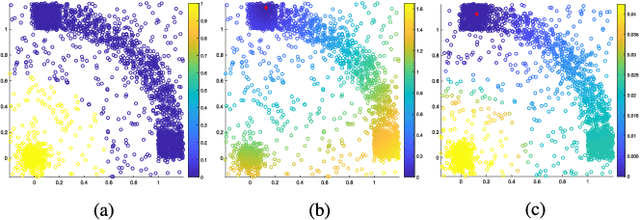
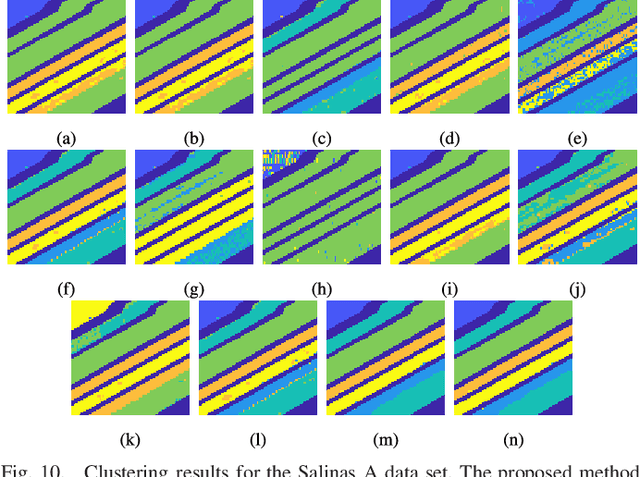
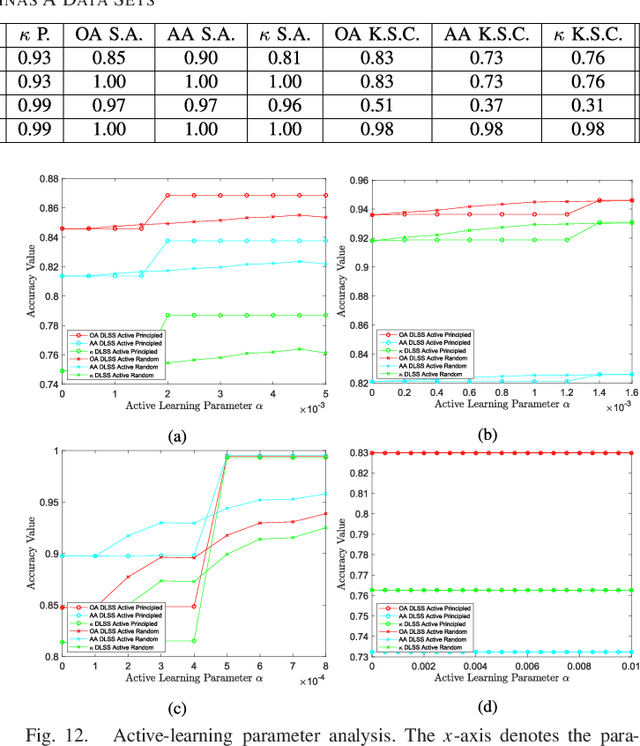
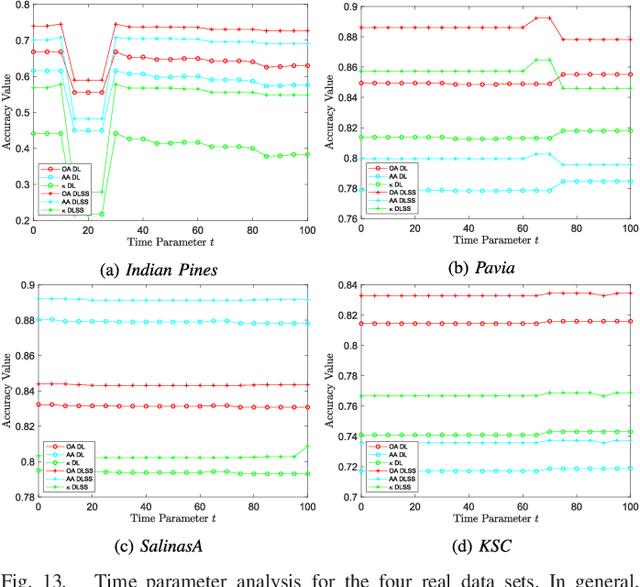
The problem of unsupervised learning and segmentation of hyperspectral images is a significant challenge in remote sensing. The high dimensionality of hyperspectral data, presence of substantial noise, and overlap of classes all contribute to the difficulty of automatically clustering and segmenting hyperspectral images. We propose an unsupervised learning technique called spectral-spatial diffusion learning (DLSS) that combines a geometric estimation of class modes with a diffusion-inspired labeling that incorporates both spectral and spatial information. The mode estimation incorporates the geometry of the hyperspectral data by using diffusion distance to promote learning a unique mode from each class. These class modes are then used to label all points by a joint spectral-spatial nonlinear diffusion process. A related variation of DLSS is also discussed, which enables active learning by requesting labels for a very small number of well-chosen pixels, dramatically boosting overall clustering results. Extensive experimental analysis demonstrates the efficacy of the proposed methods against benchmark and state-of-the-art hyperspectral analysis techniques on a variety of real datasets, their robustness to choices of parameters, and their low computational complexity.

Learning by Unsupervised Nonlinear Diffusion

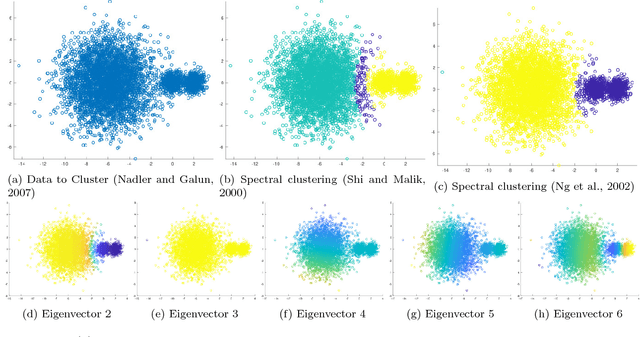
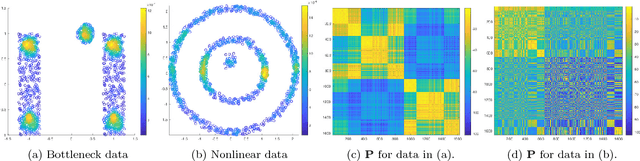
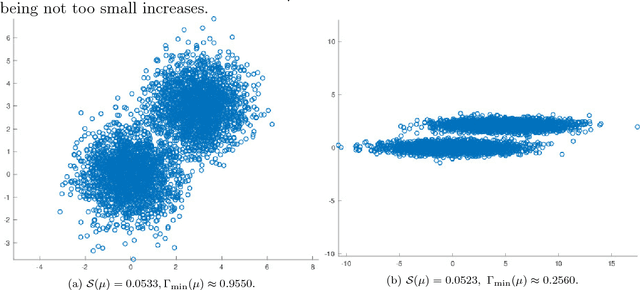
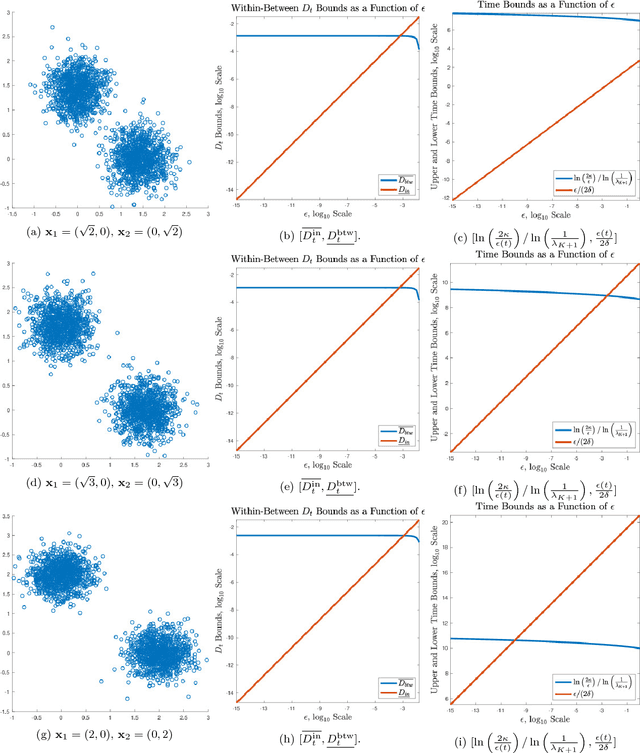
This paper proposes and analyzes a novel clustering algorithm that combines graph-based diffusion geometry with density estimation. The proposed method is suitable for data generated from mixtures of distributions with densities that are both multimodal and have nonlinear shapes. A crucial aspect of this algorithm is to introduce time of a data-adapted diffusion process as a scale parameter that is different from the local spatial scale parameter used in many clustering and learning algorithms. We prove estimates for the behavior of diffusion distances with respect to this time parameter under a flexible nonparametric data model, identifying a range of times in which the mesoscopic equilibria of the underlying process are revealed, corresponding to a gap between within-cluster and between-cluster diffusion distances. This analysis is leveraged to prove sufficient conditions guaranteeing the accuracy of the proposed learning by unsupervised nonlinear diffusion (LUND) algorithm. We implement the LUND algorithm numerically and confirm its theoretical properties on illustrative datasets, showing that the proposed method enjoys both theoretical and empirical advantages over current spectral clustering and density-based clustering techniques.

Random Projection Forests

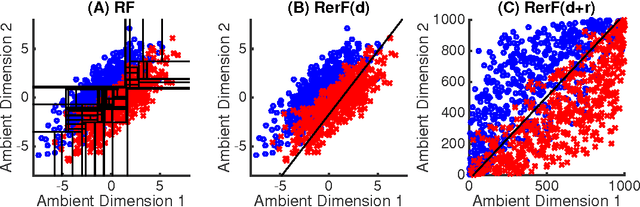
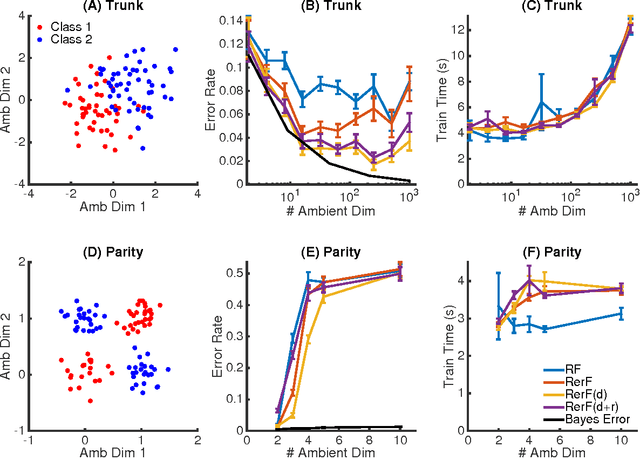
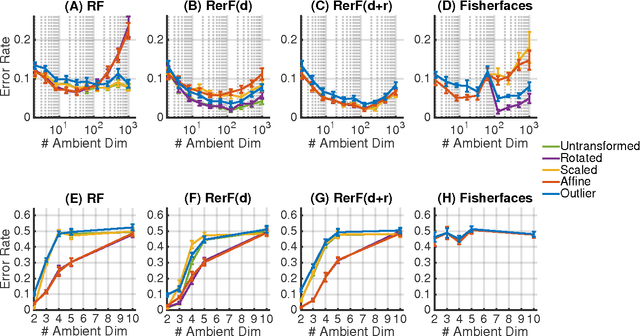
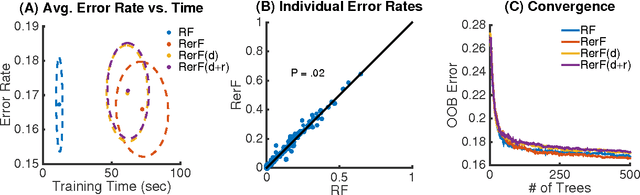
Ensemble methods---particularly those based on decision trees---have recently demonstrated superior performance in a variety of machine learning settings. We introduce a generalization of many existing decision tree methods called "Random Projection Forests" (RPF), which is any decision forest that uses (possibly data dependent and random) linear projections. Using this framework, we introduce a special case, called "Lumberjack", using very sparse random projections, that is, linear combinations of a small subset of features. Lumberjack obtains statistically significantly improved accuracy over Random Forests, Gradient Boosted Trees, and other approaches on a standard benchmark suites for classification with varying dimension, sample size, and number of classes. To illustrate how, why, and when Lumberjack outperforms other methods, we conduct extensive simulated experiments, in vectors, images, and nonlinear manifolds. Lumberjack typically yields improved performance over existing decision trees ensembles, while mitigating computational efficiency and scalability, and maintaining interpretability. Lumberjack can easily be incorporated into other ensemble methods such as boosting to obtain potentially similar gains.

Discovering and Deciphering Relationships Across Disparate Data Modalities

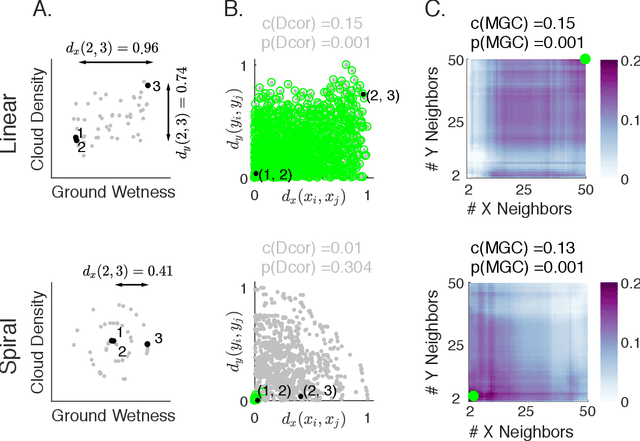
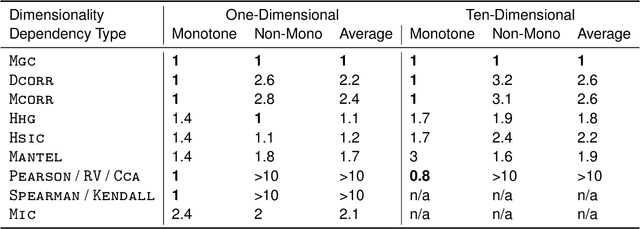
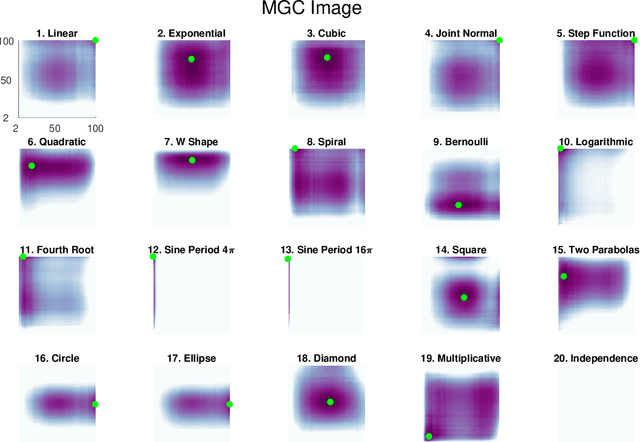
Understanding the relationships between different properties of data, such as whether a connectome or genome has information about disease status, is becoming increasingly important in modern biological datasets. While existing approaches can test whether two properties are related, they often require unfeasibly large sample sizes in real data scenarios, and do not provide any insight into how or why the procedure reached its decision. Our approach, "Multiscale Graph Correlation" (MGC), is a dependence test that juxtaposes previously disparate data science techniques, including k-nearest neighbors, kernel methods (such as support vector machines), and multiscale analysis (such as wavelets). Other methods typically require double or triple the number samples to achieve the same statistical power as MGC in a benchmark suite including high-dimensional and nonlinear relationships - spanning polynomial (linear, quadratic, cubic), trigonometric (sinusoidal, circular, ellipsoidal, spiral), geometric (square, diamond, W-shape), and other functions, with dimensionality ranging from 1 to 1000. Moreover, MGC uniquely provides a simple and elegant characterization of the potentially complex latent geometry underlying the relationship, providing insight while maintaining computational efficiency. In several real data applications, including brain imaging and cancer genetics, MGC is the only method that can both detect the presence of a dependency and provide specific guidance for the next experiment and/or analysis to conduct.

Linear Optimal Low Rank Projection for High-Dimensional Multi-Class Data

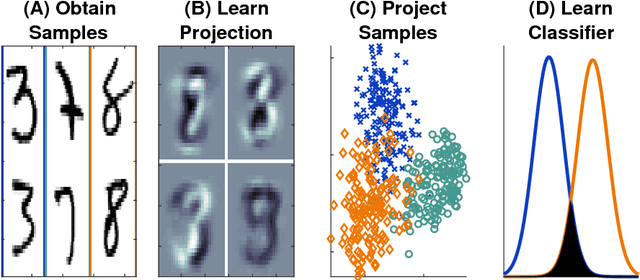
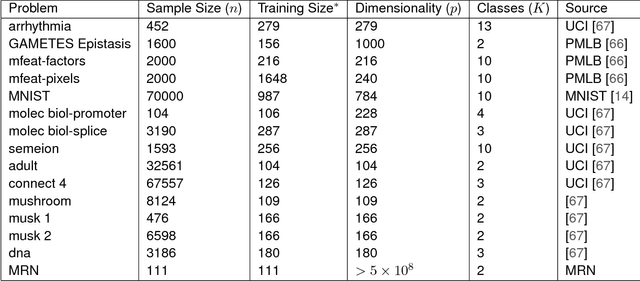
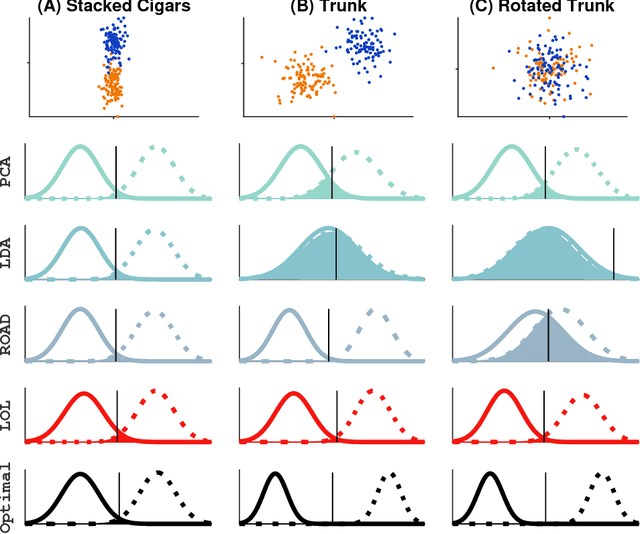
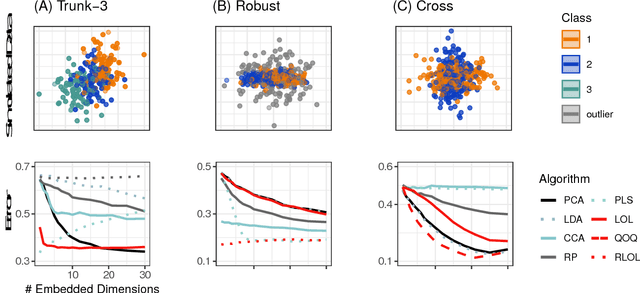
Classifying samples into categories becomes intractable when a single sample can have millions to billions of features, such as in genetics or imaging data. Principal Components Analysis (PCA) is widely used to identify a low-dimensional representation of such features for further analysis. However, PCA ignores class labels, such as whether or not a subject has cancer, thereby discarding information that could substantially improve downstream classification performance. We describe an approach, "Linear Optimal Low-rank" projection (LOL), which extends PCA by incorporating the class labels in a fashion that is advantageous over existing supervised dimensionality reduction techniques. We prove, and substantiate with synthetic experiments, that LOL leads to a better representation of the data for subsequent classification than other linear approaches, while adding negligible computational cost. We then demonstrate that LOL substantially outperforms PCA in differentiating cancer patients from healthy controls using genetic data, and in differentiating gender using magnetic resonance imaging data with $>$500 million features and 400 gigabytes of data. LOL therefore allows the solution of previous intractable problems, yet requires only a few minutes to run on a desktop computer.

Path-Based Spectral Clustering: Guarantees, Robustness to Outliers, and Fast Algorithms

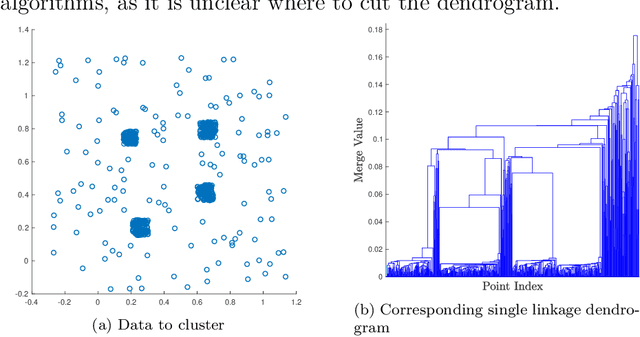
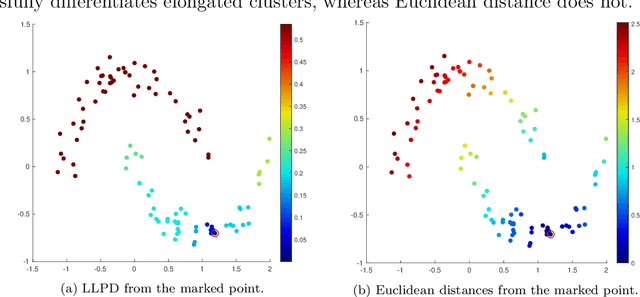
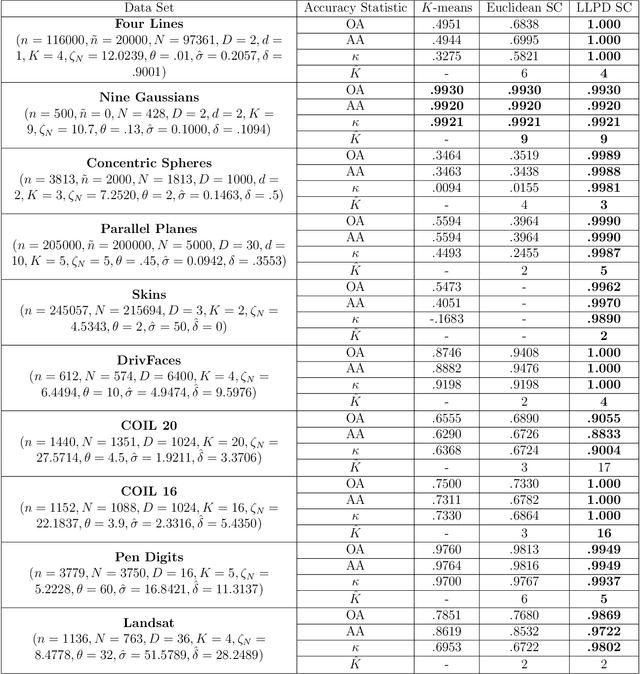
We consider the problem of clustering with the longest leg path distance (LLPD) metric, which is informative for elongated and irregularly shaped clusters. We prove finite-sample guarantees on the performance of clustering with respect to this metric when random samples are drawn from multiple intrinsically low-dimensional clusters in high-dimensional space, in the presence of a large number of high-dimensional outliers. By combining these results with spectral clustering with respect to LLPD, we provide conditions under which the eigengap statistic correctly determines the number of clusters for a large class of data sets, and prove guarantees on the number of points mislabeled by the proposed algorithm. Our methods are quite general and provide performance guarantees for spectral clustering with any ultrametric. We also introduce an efficient approximation algorithm, easy to implement, for the LLPD, based on a multiscale analysis of adjacency graphs.

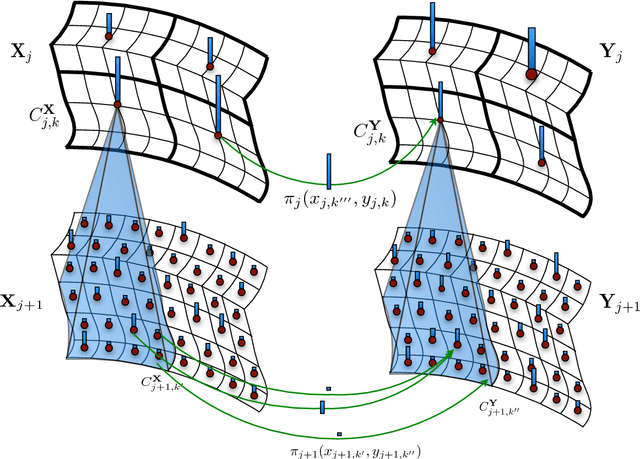
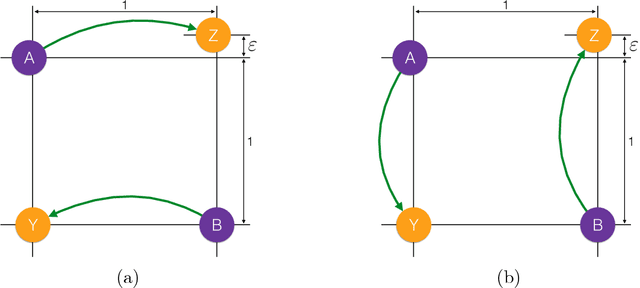
Multiscale Strategies for Computing Optimal Transport

This paper presents a multiscale approach to efficiently compute approximate optimal transport plans between point sets. It is particularly well-suited for point sets that are in high-dimensions, but are close to being intrinsically low-dimensional. The approach is based on an adaptive multiscale decomposition of the point sets. The multiscale decomposition yields a sequence of optimal transport problems, that are solved in a top-to-bottom fashion from the coarsest to the finest scale. We provide numerical evidence that this multiscale approach scales approximately linearly, in time and memory, in the number of nodes, instead of quadratically or worse for a direct solution. Empirically, the multiscale approach results in less than one percent relative error in the objective function. Furthermore, the multiscale plans constructed are of interest by themselves as they may be used to introduce novel features and notions of distances between point sets. An analysis of sets of brain MRI based on optimal transport distances illustrates the effectiveness of the proposed method on a real world data set. The application demonstrates that multiscale optimal transport distances have the potential to improve on state-of-the-art metrics currently used in computational anatomy.

Adaptive Geometric Multiscale Approximations for Intrinsically Low-dimensional Data

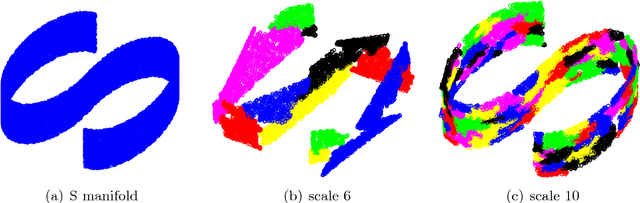
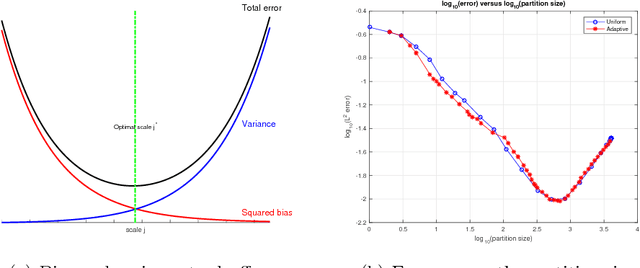
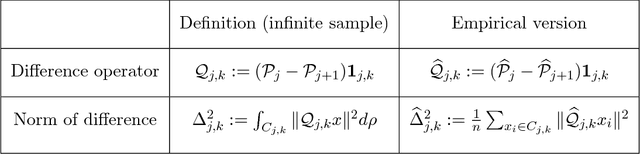
We consider the problem of efficiently approximating and encoding high-dimensional data sampled from a probability distribution $\rho$ in $\mathbb{R}^D$, that is nearly supported on a $d$-dimensional set $\mathcal{M}$ - for example supported on a $d$-dimensional Riemannian manifold. Geometric Multi-Resolution Analysis (GMRA) provides a robust and computationally efficient procedure to construct low-dimensional geometric approximations of $\mathcal{M}$ at varying resolutions. We introduce a thresholding algorithm on the geometric wavelet coefficients, leading to what we call adaptive GMRA approximations. We show that these data-driven, empirical approximations perform well, when the threshold is chosen as a suitable universal function of the number of samples $n$, on a wide variety of measures $\rho$, that are allowed to exhibit different regularity at different scales and locations, thereby efficiently encoding data from more complex measures than those supported on manifolds. These approximations yield a data-driven dictionary, together with a fast transform mapping data to coefficients, and an inverse of such a map. The algorithms for both the dictionary construction and the transforms have complexity $C n \log n$ with the constant linear in $D$ and exponential in $d$. Our work therefore establishes adaptive GMRA as a fast dictionary learning algorithm with approximation guarantees. We include several numerical experiments on both synthetic and real data, confirming our theoretical results and demonstrating the effectiveness of adaptive GMRA.