Differentially Private SGD with Sparse Gradients

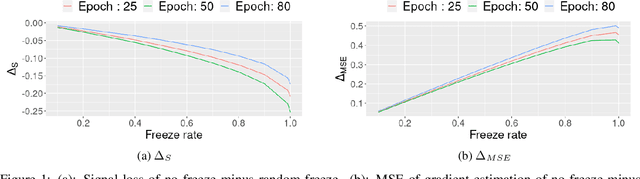
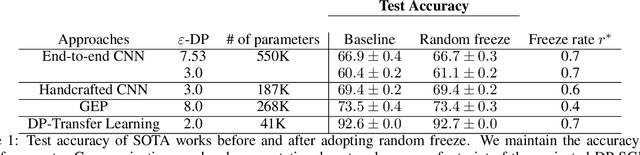
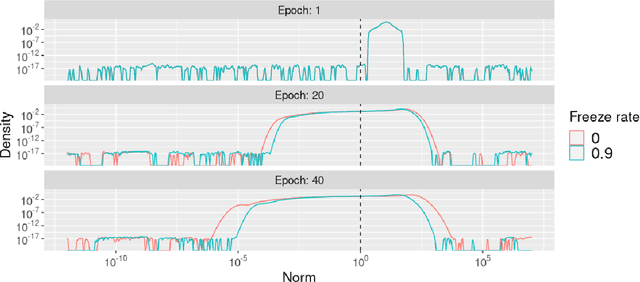
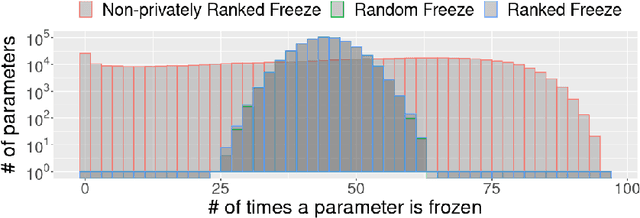
To protect sensitive training data, differentially private stochastic gradient descent (DP-SGD) has been adopted in deep learning to provide rigorously defined privacy. However, DP-SGD requires the injection of an amount of noise that scales with the number of gradient dimensions, resulting in large performance drops compared to non-private training. In this work, we propose random freeze which randomly freezes a progressively increasing subset of parameters and results in sparse gradient updates while maintaining or increasing accuracy. We theoretically prove the convergence of random freeze and find that random freeze exhibits a signal loss and perturbation moderation trade-off in DP-SGD. Applying random freeze across various DP-SGD frameworks, we maintain accuracy within the same number of iterations while achieving up to 70% representation sparsity, which demonstrates that the trade-off exists in a variety of DP-SGD methods. We further note that random freeze significantly improves accuracy, in particular for large networks. Additionally, axis-aligned sparsity induced by random freeze leads to various advantages for projected DP-SGD or federated learning in terms of computational cost, memory footprint and communication overhead.

R-GAP: Recursive Gradient Attack on Privacy

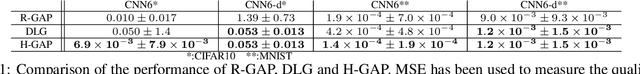
Federated learning frameworks have been regarded as a promising approach to break the dilemma between demands on privacy and the promise of learning from large collections of distributed data. Many such frameworks only ask collaborators to share their local update of a common model, i.e. gradients with respect to locally stored data, instead of exposing their raw data to other collaborators. However, recent optimization-based gradient attacks show that raw data can often be accurately recovered from gradients. It has been shown that minimizing the Euclidean distance between true gradients and those calculated from estimated data is often effective in fully recovering private data. However, there is a fundamental lack of theoretical understanding of how and when gradients can lead to unique recovery of original data. Our research fills this gap by providing a closed-form recursive procedure to recover data from gradients in deep neural networks. We demonstrate that gradient attacks consist of recursively solving a sequence of systems of linear equations. Furthermore, our closed-form approach works as well as or even better than optimization-based approaches at a fraction of the computation, we name it Recursive Gradient Attack on Privacy (R-GAP). Additionally, we propose a rank analysis method, which can be used to estimate a network architecture's risk of a gradient attack. Experimental results demonstrate the validity of the closed-form attack and rank analysis, while demonstrating its superior computational properties and lack of susceptibility to local optima vis a vis optimization-based attacks. Source code is available for download from https://github.com/JunyiZhu-AI/R-GAP.

Commands 4 Autonomous Vehicles (C4AV) Workshop Summary

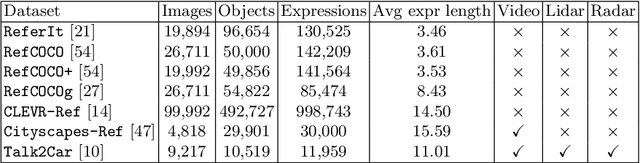
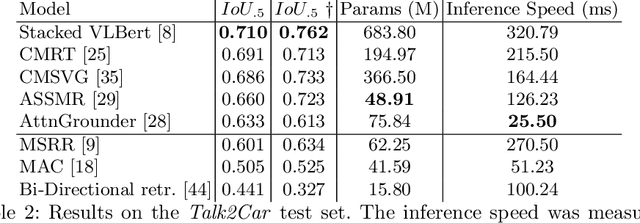
The task of visual grounding requires locating the most relevant region or object in an image, given a natural language query. So far, progress on this task was mostly measured on curated datasets, which are not always representative of human spoken language. In this work, we deviate from recent, popular task settings and consider the problem under an autonomous vehicle scenario. In particular, we consider a situation where passengers can give free-form natural language commands to a vehicle which can be associated with an object in the street scene. To stimulate research on this topic, we have organized the \emph{Commands for Autonomous Vehicles} (C4AV) challenge based on the recent \emph{Talk2Car} dataset (URL: https://www.aicrowd.com/challenges/eccv-2020-commands-4-autonomous-vehicles). This paper presents the results of the challenge. First, we compare the used benchmark against existing datasets for visual grounding. Second, we identify the aspects that render top-performing models successful, and relate them to existing state-of-the-art models for visual grounding, in addition to detecting potential failure cases by evaluating on carefully selected subsets. Finally, we discuss several possibilities for future work.

Semixup: In- and Out-of-Manifold Regularization for Deep Semi-Supervised Knee Osteoarthritis Severity Grading from Plain Radiographs

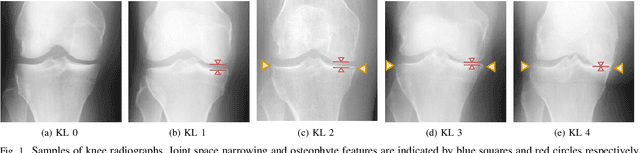
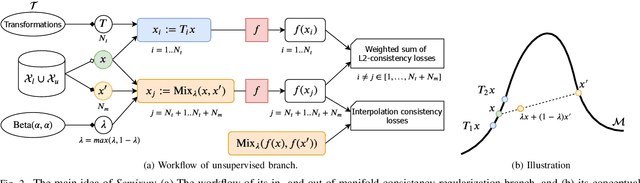
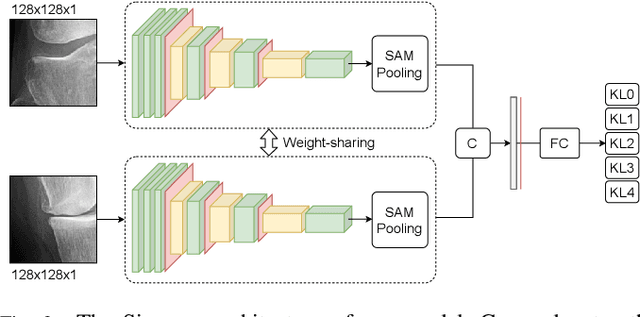
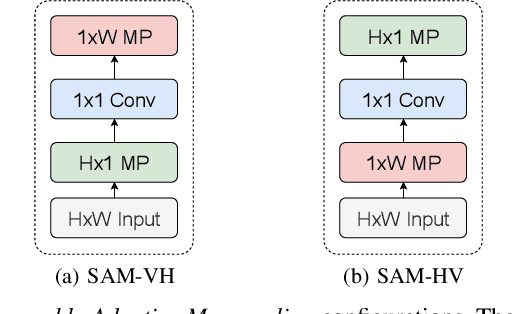
Knee osteoarthritis (OA) is one of the highest disability factors in the world in humans. This musculoskeletal disorder is assessed from clinical symptoms, and typically confirmed via radiographic assessment. This visual assessment done by a radiologist requires experience, and suffers from high inter-observer variability. The recent development in the literature has shown that deep learning (DL) methods can reliably perform the OA severity assessment according to the gold standard Kellgren-Lawrence (KL) grading system. However, these methods require large amounts of labeled data, which are costly to obtain. In this study, we propose the Semixup algorithm, a semi-supervised learning (SSL) approach to leverage unlabeled data. Semixup relies on consistency regularization using in- and out-of-manifold samples, together with interpolated consistency. On an independent test set, our method significantly outperformed other state-of-the-art SSL methods in most cases, and even achieved a comparable performance to a well-tuned fully supervised learning (SL) model that required over 12 times more labeled data.

Optimizing the Dice Score and Jaccard Index for Medical Image Segmentation: Theory & Practice

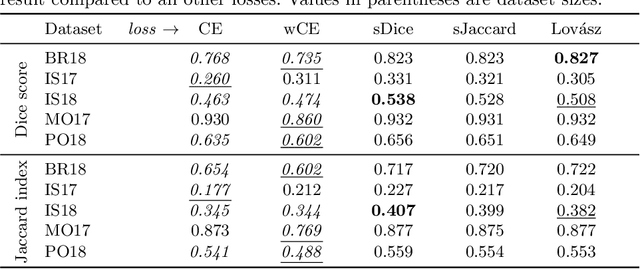
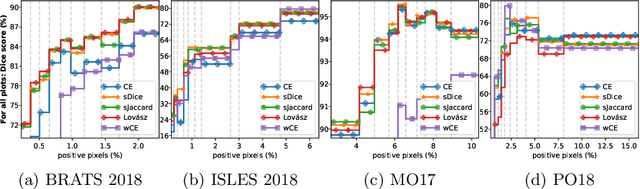
The Dice score and Jaccard index are commonly used metrics for the evaluation of segmentation tasks in medical imaging. Convolutional neural networks trained for image segmentation tasks are usually optimized for (weighted) cross-entropy. This introduces an adverse discrepancy between the learning optimization objective (the loss) and the end target metric. Recent works in computer vision have proposed soft surrogates to alleviate this discrepancy and directly optimize the desired metric, either through relaxations (soft-Dice, soft-Jaccard) or submodular optimization (Lov\'asz-softmax). The aim of this study is two-fold. First, we investigate the theoretical differences in a risk minimization framework and question the existence of a weighted cross-entropy loss with weights theoretically optimized to surrogate Dice or Jaccard. Second, we empirically investigate the behavior of the aforementioned loss functions w.r.t. evaluation with Dice score and Jaccard index on five medical segmentation tasks. Through the application of relative approximation bounds, we show that all surrogates are equivalent up to a multiplicative factor, and that no optimal weighting of cross-entropy exists to approximate Dice or Jaccard measures. We validate these findings empirically and show that, while it is important to opt for one of the target metric surrogates rather than a cross-entropy-based loss, the choice of the surrogate does not make a statistical difference on a wide range of medical segmentation tasks.

Generating superpixels using deep image representations

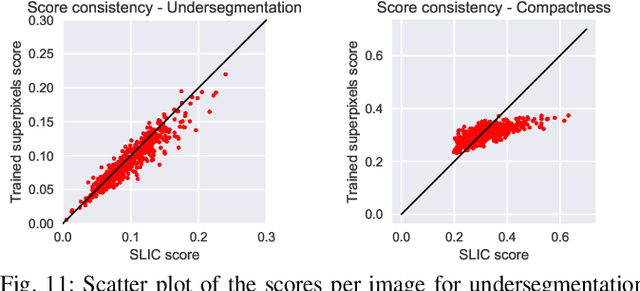
Superpixel algorithms are a common pre-processing step for computer vision algorithms such as segmentation, object tracking and localization. Many superpixel methods only rely on colors features for segmentation, limiting performance in low-contrast regions and applicability to infrared or medical images where object boundaries have wide appearance variability. We study the inclusion of deep image features in the SLIC superpixel algorithm to exploit higher-level image representations. In addition, we devise a trainable superpixel algorithm, yielding an intermediate domain-specific image representation that can be applied to different tasks. A clustering-based superpixel algorithm is transformed into a pixel-wise classification task and superpixel training data is derived from semantic segmentation datasets. Our results demonstrate that this approach is able to improve superpixel quality consistently.

Scattering Networks for Hybrid Representation Learning

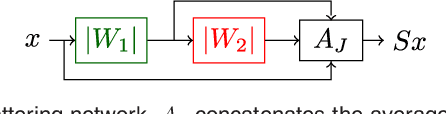
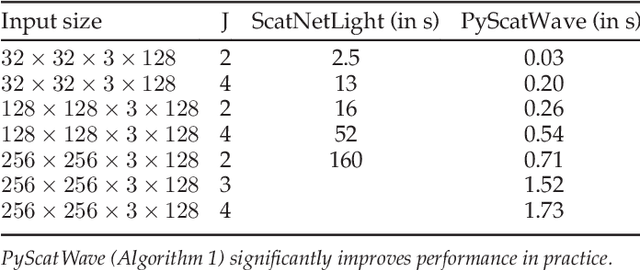
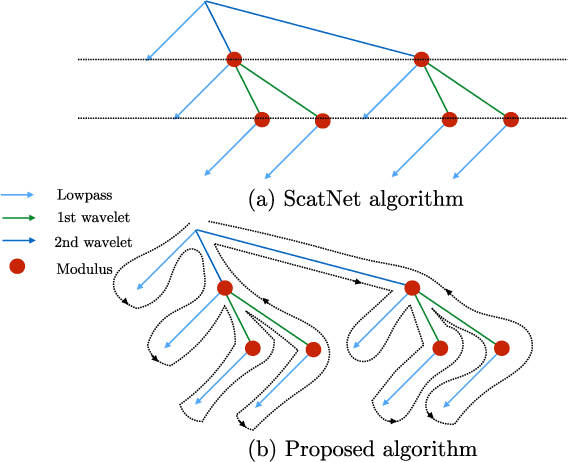
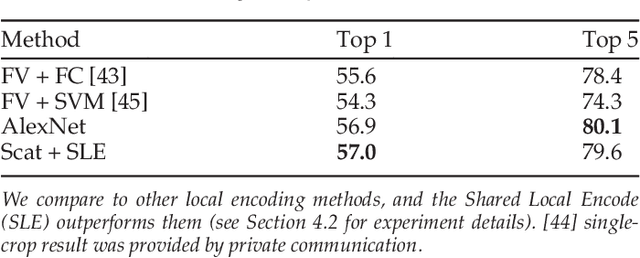
Scattering networks are a class of designed Convolutional Neural Networks (CNNs) with fixed weights. We argue they can serve as generic representations for modelling images. In particular, by working in scattering space, we achieve competitive results both for supervised and unsupervised learning tasks, while making progress towards constructing more interpretable CNNs. For supervised learning, we demonstrate that the early layers of CNNs do not necessarily need to be learned, and can be replaced with a scattering network instead. Indeed, using hybrid architectures, we achieve the best results with predefined representations to-date, while being competitive with end-to-end learned CNNs. Specifically, even applying a shallow cascade of small-windowed scattering coefficients followed by 1$\times$1-convolutions results in AlexNet accuracy on the ILSVRC2012 classification task. Moreover, by combining scattering networks with deep residual networks, we achieve a single-crop top-5 error of 11.4% on ILSVRC2012. Also, we show they can yield excellent performance in the small sample regime on CIFAR-10 and STL-10 datasets, exceeding their end-to-end counterparts, through their ability to incorporate geometrical priors. For unsupervised learning, scattering coefficients can be a competitive representation that permits image recovery. We use this fact to train hybrid GANs to generate images. Finally, we empirically analyze several properties related to stability and reconstruction of images from scattering coefficients.

Learning to Discover Sparse Graphical Models

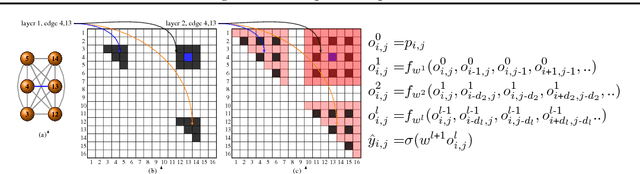
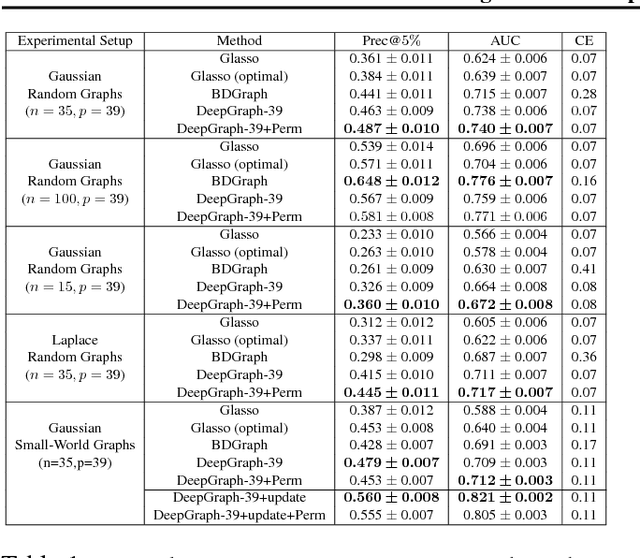
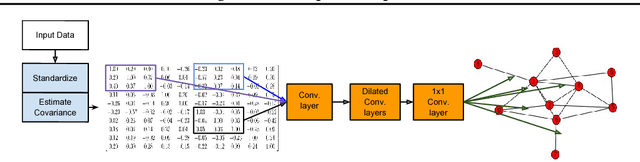
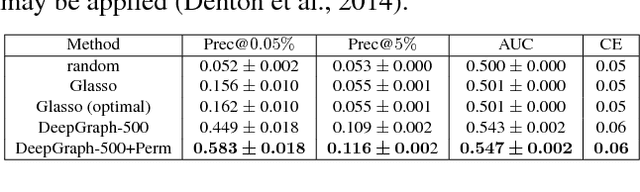
We consider structure discovery of undirected graphical models from observational data. Inferring likely structures from few examples is a complex task often requiring the formulation of priors and sophisticated inference procedures. Popular methods rely on estimating a penalized maximum likelihood of the precision matrix. However, in these approaches structure recovery is an indirect consequence of the data-fit term, the penalty can be difficult to adapt for domain-specific knowledge, and the inference is computationally demanding. By contrast, it may be easier to generate training samples of data that arise from graphs with the desired structure properties. We propose here to leverage this latter source of information as training data to learn a function, parametrized by a neural network that maps empirical covariance matrices to estimated graph structures. Learning this function brings two benefits: it implicitly models the desired structure or sparsity properties to form suitable priors, and it can be tailored to the specific problem of edge structure discovery, rather than maximizing data likelihood. Applying this framework, we find our learnable graph-discovery method trained on synthetic data generalizes well: identifying relevant edges in both synthetic and real data, completely unknown at training time. We find that on genetics, brain imaging, and simulation data we obtain performance generally superior to analytical methods.

The Lovász Hinge: A Novel Convex Surrogate for Submodular Losses

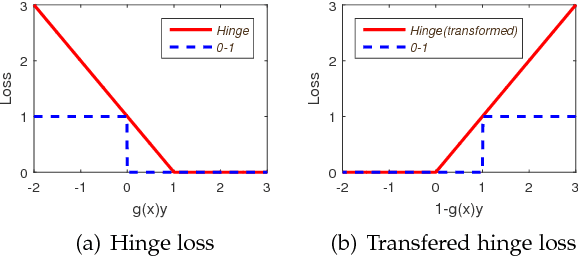
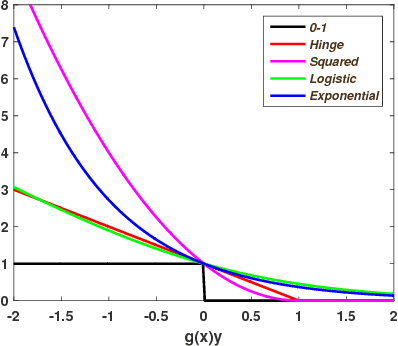
Learning with non-modular losses is an important problem when sets of predictions are made simultaneously. The main tools for constructing convex surrogate loss functions for set prediction are margin rescaling and slack rescaling. In this work, we show that these strategies lead to tight convex surrogates iff the underlying loss function is increasing in the number of incorrect predictions. However, gradient or cutting-plane computation for these functions is NP-hard for non-supermodular loss functions. We propose instead a novel surrogate loss function for submodular losses, the Lov\'asz hinge, which leads to O(p log p) complexity with O(p) oracle accesses to the loss function to compute a gradient or cutting-plane. We prove that the Lov\'asz hinge is convex and yields an extension. As a result, we have developed the first tractable convex surrogates in the literature for submodular losses. We demonstrate the utility of this novel convex surrogate through several set prediction tasks, including on the PASCAL VOC and Microsoft COCO datasets.

A Convex Surrogate Operator for General Non-Modular Loss Functions

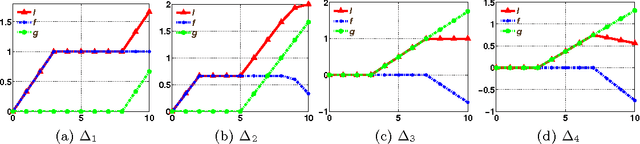
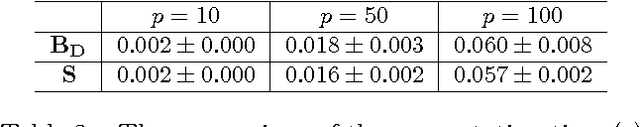
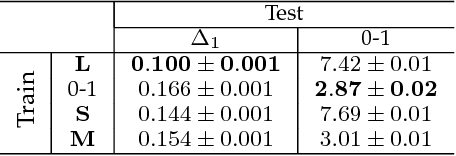
Empirical risk minimization frequently employs convex surrogates to underlying discrete loss functions in order to achieve computational tractability during optimization. However, classical convex surrogates can only tightly bound modular loss functions, sub-modular functions or supermodular functions separately while maintaining polynomial time computation. In this work, a novel generic convex surrogate for general non-modular loss functions is introduced, which provides for the first time a tractable solution for loss functions that are neither super-modular nor submodular. This convex surro-gate is based on a submodular-supermodular decomposition for which the existence and uniqueness is proven in this paper. It takes the sum of two convex surrogates that separately bound the supermodular component and the submodular component using slack-rescaling and the Lov{\'a}sz hinge, respectively. It is further proven that this surrogate is convex , piecewise linear, an extension of the loss function, and for which subgradient computation is polynomial time. Empirical results are reported on a non-submodular loss based on the S{{\o}}rensen-Dice difference function, and a real-world face track dataset with tens of thousands of frames, demonstrating the improved performance, efficiency, and scalabil-ity of the novel convex surrogate.