Reducing Neural Architecture Search Spaces with Training-Free Statistics and Computational Graph Clustering

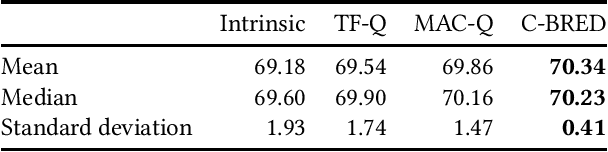
The computational demands of neural architecture search (NAS) algorithms are usually directly proportional to the size of their target search spaces. Thus, limiting the search to high-quality subsets can greatly reduce the computational load of NAS algorithms. In this paper, we present Clustering-Based REDuction (C-BRED), a new technique to reduce the size of NAS search spaces. C-BRED reduces a NAS space by clustering the computational graphs associated with its architectures and selecting the most promising cluster using proxy statistics correlated with network accuracy. When considering the NAS-Bench-201 (NB201) data set and the CIFAR-100 task, C-BRED selects a subset with 70% average accuracy instead of the whole space's 64% average accuracy.

Training Quantised Neural Networks with STE Variants: the Additive Noise Annealing Algorithm

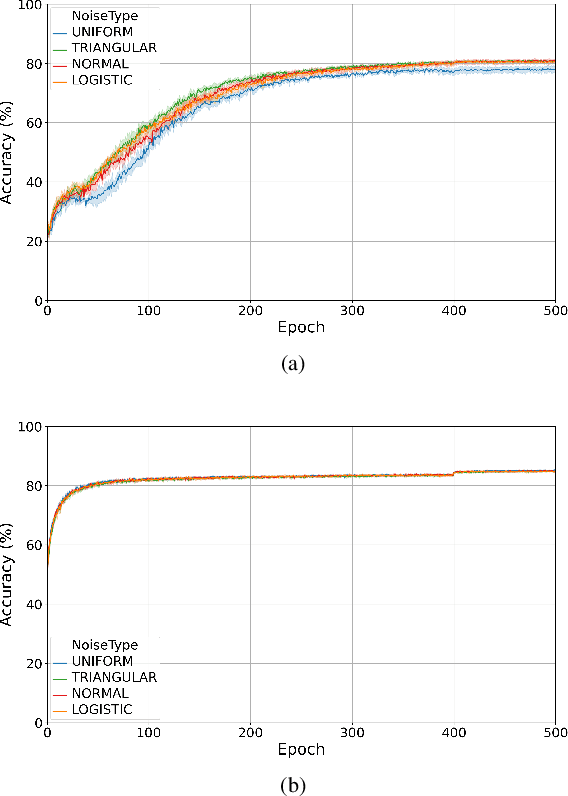
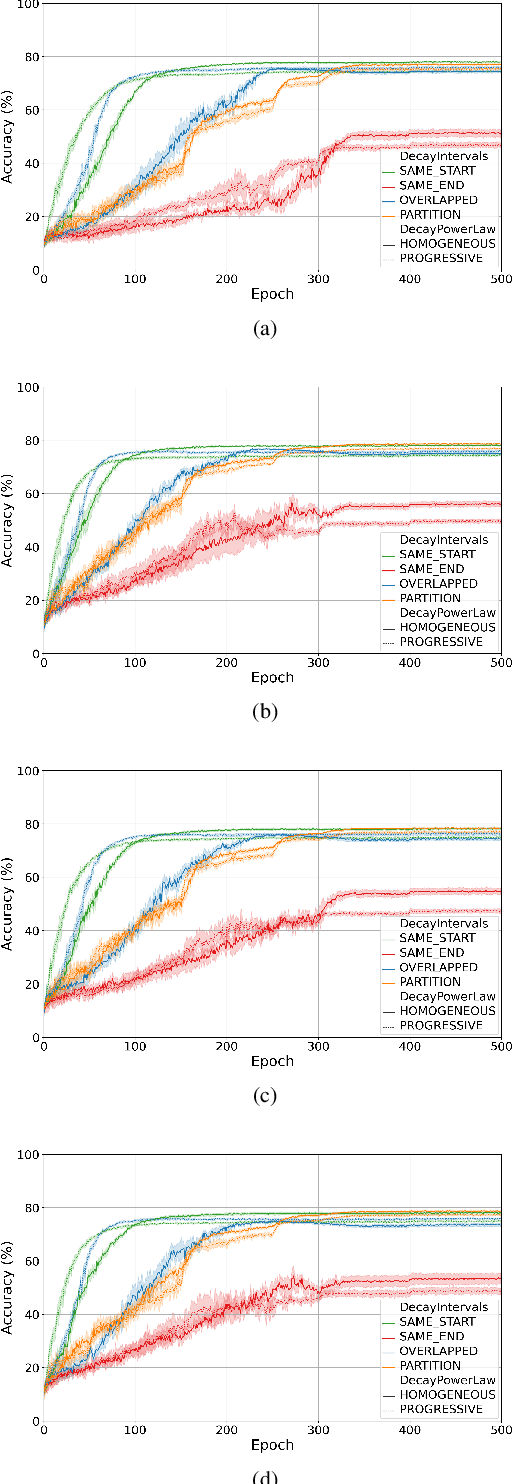
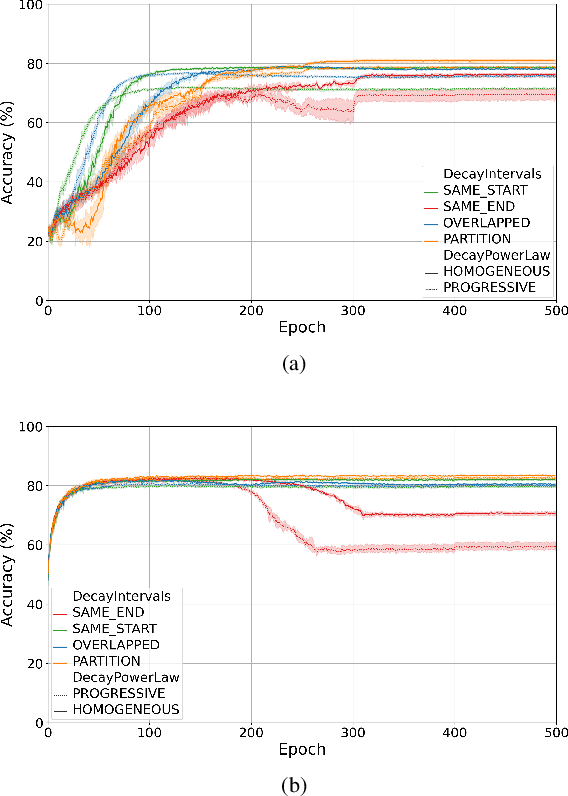
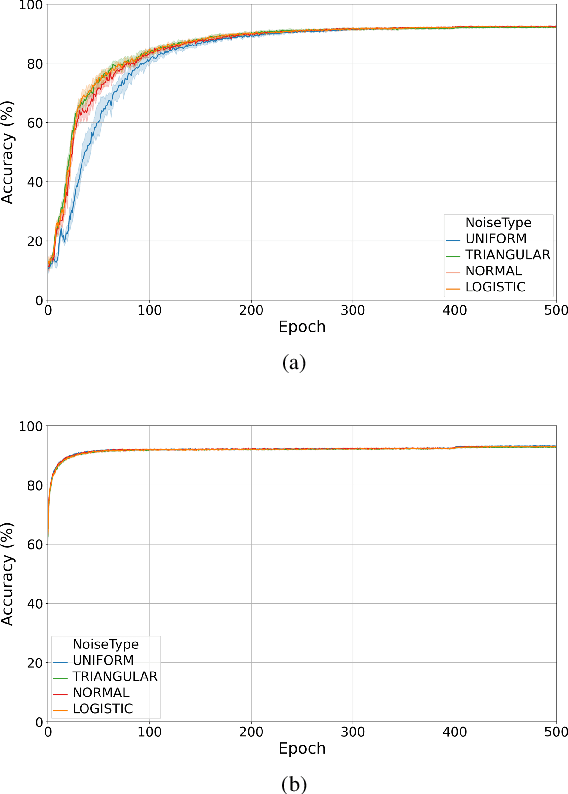
Training quantised neural networks (QNNs) is a non-differentiable optimisation problem since weights and features are output by piecewise constant functions. The standard solution is to apply the straight-through estimator (STE), using different functions during the inference and gradient computation steps. Several STE variants have been proposed in the literature aiming to maximise the task accuracy of the trained network. In this paper, we analyse STE variants and study their impact on QNN training. We first observe that most such variants can be modelled as stochastic regularisations of stair functions; although this intuitive interpretation is not new, our rigorous discussion generalises to further variants. Then, we analyse QNNs mixing different regularisations, finding that some suitably synchronised smoothing of each layer map is required to guarantee pointwise compositional convergence to the target discontinuous function. Based on these theoretical insights, we propose additive noise annealing (ANA), a new algorithm to train QNNs encompassing standard STE and its variants as special cases. When testing ANA on the CIFAR-10 image classification benchmark, we find that the major impact on task accuracy is not due to the qualitative shape of the regularisations but to the proper synchronisation of the different STE variants used in a network, in accordance with the theoretical results.

ZippyPoint: Fast Interest Point Detection, Description, and Matching through Mixed Precision Discretization

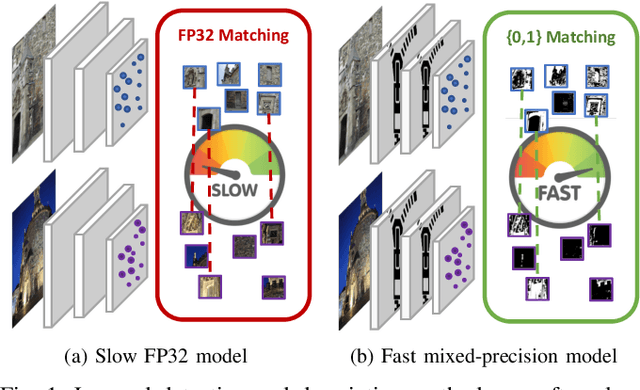
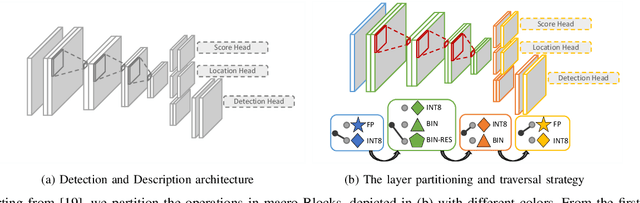
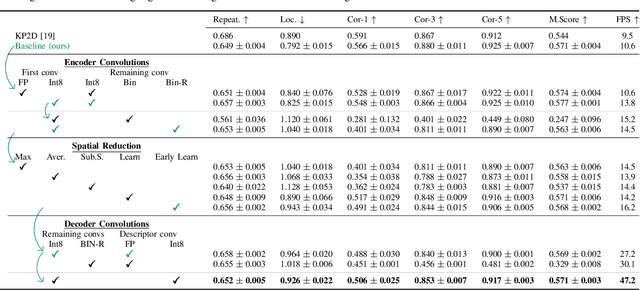
The design of more complex and powerful neural network models has significantly advanced the state-of-the-art in local feature detection and description. These advances can be attributed to deeper networks, improved training methodologies through self-supervision, or the introduction of new building blocks, such as graph neural networks for feature matching. However, in the pursuit of increased performance, efficient architectures that generate lightweight descriptors have received surprisingly little attention. In this paper, we investigate the adaptations neural networks for detection and description require in order to enable their use in embedded platforms. To that end, we investigate and adapt network quantization techniques for use in real-time applications. In addition, we revisit common practices in descriptor quantization and propose the use of a binary descriptor normalization layer, enabling the generation of distinctive length-invariant binary descriptors. ZippyPoint, our efficient network, runs at 47.2 fps on the Apple M1 CPU. This is up to 5x faster than other learned detection and description models, making it the only real-time learned network. ZippyPoint consistently outperforms all other binary detection and descriptor methods in visual localization and homography estimation tasks. Code and trained models will be released upon publication.

Proceedings of the DATE Friday Workshop on System-level Design Methods for Deep Learning on Heterogeneous Architectures

This volume contains the papers accepted at the first DATE Friday Workshop on System-level Design Methods for Deep Learning on Heterogeneous Architectures (SLOHA 2021), held virtually on February 5, 2021. SLOHA 2021 was co-located with the Conference on Design, Automation and Test in Europe (DATE).

Analytical aspects of non-differentiable neural networks

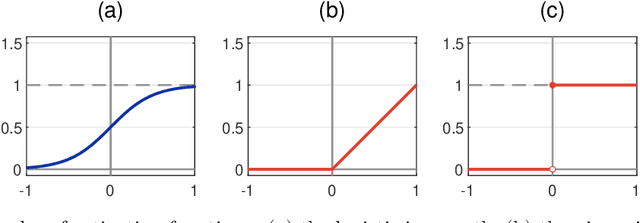
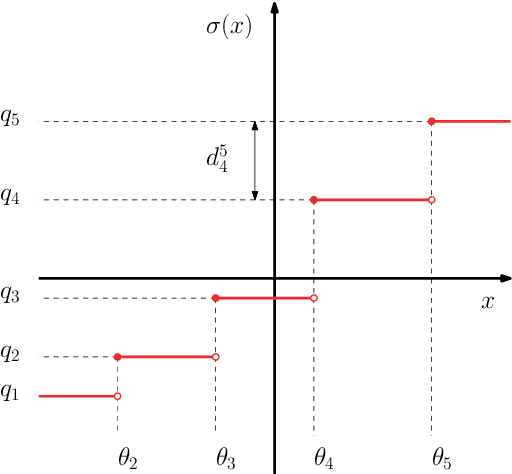
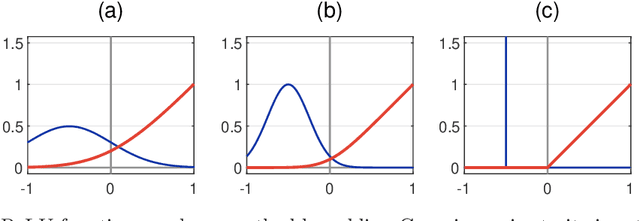
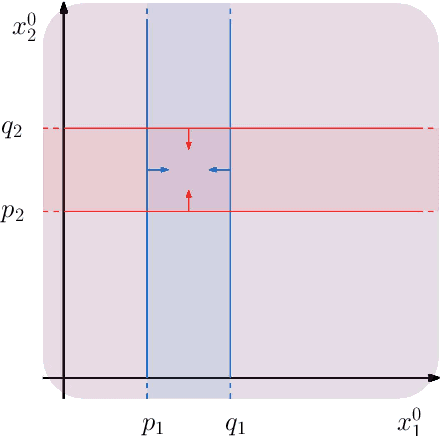
Research in computational deep learning has directed considerable efforts towards hardware-oriented optimisations for deep neural networks, via the simplification of the activation functions, or the quantization of both activations and weights. The resulting non-differentiability (or even discontinuity) of the networks poses some challenging problems, especially in connection with the learning process. In this paper, we address several questions regarding both the expressivity of quantized neural networks and approximation techniques for non-differentiable networks. First, we answer in the affirmative the question of whether QNNs have the same expressivity as DNNs in terms of approximation of Lipschitz functions in the $L^{\infty}$ norm. Then, considering a continuous but not necessarily differentiable network, we describe a layer-wise stochastic regularisation technique to produce differentiable approximations, and we show how this approach to regularisation provides elegant quantitative estimates. Finally, we consider networks defined by means of Heaviside-type activation functions, and prove for them a pointwise approximation result by means of smooth networks under suitable assumptions on the regularised activations.

Additive Noise Annealing and Approximation Properties of Quantized Neural Networks

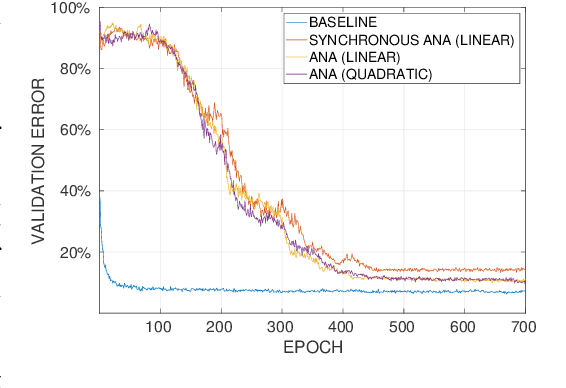
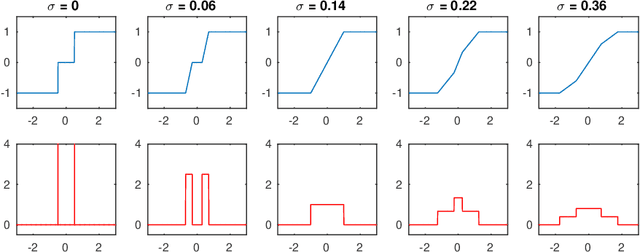
We present a theoretical and experimental investigation of the quantization problem for artificial neural networks. We provide a mathematical definition of quantized neural networks and analyze their approximation capabilities, showing in particular that any Lipschitz-continuous map defined on a hypercube can be uniformly approximated by a quantized neural network. We then focus on the regularization effect of additive noise on the arguments of multi-step functions inherent to the quantization of continuous variables. In particular, when the expectation operator is applied to a non-differentiable multi-step random function, and if the underlying probability density is differentiable (in either classical or weak sense), then a differentiable function is retrieved, with explicit bounds on its Lipschitz constant. Based on these results, we propose a novel gradient-based training algorithm for quantized neural networks that generalizes the straight-through estimator, acting on noise applied to the network's parameters. We evaluate our algorithm on the CIFAR-10 and ImageNet image classification benchmarks, showing state-of-the-art performance on AlexNet and MobileNetV2 for ternary networks.