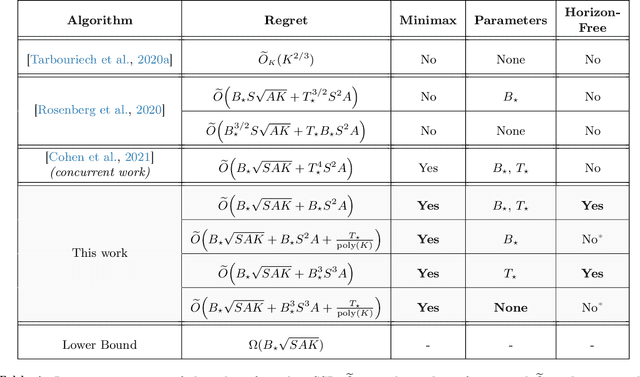
Stochastic Shortest Path: Minimax, Parameter-Free and Towards Horizon-Free Regret

We study the problem of learning in the stochastic shortest path (SSP) setting, where an agent seeks to minimize the expected cost accumulated before reaching a goal state. We design a novel model-based algorithm EB-SSP that carefully skews the empirical transitions and perturbs the empirical costs with an exploration bonus to guarantee both optimism and convergence of the associated value iteration scheme. We prove that EB-SSP achieves the minimax regret rate $\widetilde{O}(B_{\star} \sqrt{S A K})$, where $K$ is the number of episodes, $S$ is the number of states, $A$ is the number of actions and $B_{\star}$ bounds the expected cumulative cost of the optimal policy from any state, thus closing the gap with the lower bound. Interestingly, EB-SSP obtains this result while being parameter-free, i.e., it does not require any prior knowledge of $B_{\star}$, nor of $T_{\star}$ which bounds the expected time-to-goal of the optimal policy from any state. Furthermore, we illustrate various cases (e.g., positive costs, or general costs when an order-accurate estimate of $T_{\star}$ is available) where the regret only contains a logarithmic dependence on $T_{\star}$, thus yielding the first horizon-free regret bound beyond the finite-horizon MDP setting.

Leveraging Good Representations in Linear Contextual Bandits

The linear contextual bandit literature is mostly focused on the design of efficient learning algorithms for a given representation. However, a contextual bandit problem may admit multiple linear representations, each one with different characteristics that directly impact the regret of the learning algorithm. In particular, recent works showed that there exist "good" representations for which constant problem-dependent regret can be achieved. In this paper, we first provide a systematic analysis of the different definitions of "good" representations proposed in the literature. We then propose a novel selection algorithm able to adapt to the best representation in a set of $M$ candidates. We show that the regret is indeed never worse than the regret obtained by running LinUCB on the best representation (up to a $\ln M$ factor). As a result, our algorithm achieves constant regret whenever a "good" representation is available in the set. Furthermore, we show that the algorithm may still achieve constant regret by implicitly constructing a "good" representation, even when none of the initial representations is "good". Finally, we empirically validate our theoretical findings in a number of standard contextual bandit problems.

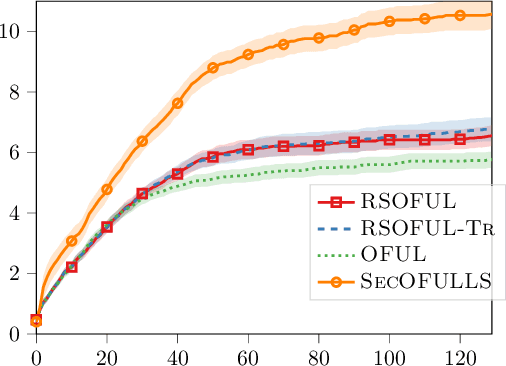
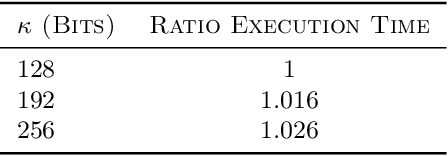
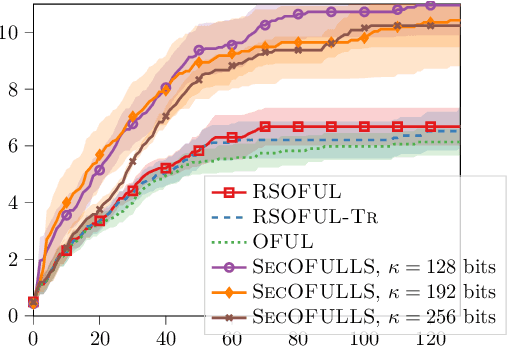
Homomorphically Encrypted Linear Contextual Bandit

Contextual bandit is a general framework for online learning in sequential decision-making problems that has found application in a large range of domains, including recommendation system, online advertising, clinical trials and many more. A critical aspect of bandit methods is that they require to observe the contexts -- i.e., individual or group-level data -- and the rewards in order to solve the sequential problem. The large deployment in industrial applications has increased interest in methods that preserve the privacy of the users. In this paper, we introduce a privacy-preserving bandit framework based on asymmetric encryption. The bandit algorithm only observes encrypted information (contexts and rewards) and has no ability to decrypt it. Leveraging homomorphic encryption, we show that despite the complexity of the setting, it is possible to learn over encrypted data. We introduce an algorithm that achieves a $\widetilde{O}(d\sqrt{T})$ regret bound in any linear contextual bandit problem, while keeping data encrypted.

Improved Sample Complexity for Incremental Autonomous Exploration in MDPs

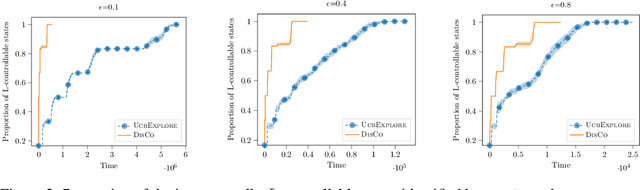
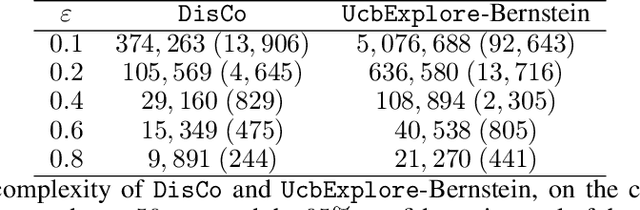
We investigate the exploration of an unknown environment when no reward function is provided. Building on the incremental exploration setting introduced by Lim and Auer [1], we define the objective of learning the set of $\epsilon$-optimal goal-conditioned policies attaining all states that are incrementally reachable within $L$ steps (in expectation) from a reference state $s_0$. In this paper, we introduce a novel model-based approach that interleaves discovering new states from $s_0$ and improving the accuracy of a model estimate that is used to compute goal-conditioned policies to reach newly discovered states. The resulting algorithm, DisCo, achieves a sample complexity scaling as $\tilde{O}(L^5 S_{L+\epsilon} \Gamma_{L+\epsilon} A \epsilon^{-2})$, where $A$ is the number of actions, $S_{L+\epsilon}$ is the number of states that are incrementally reachable from $s_0$ in $L+\epsilon$ steps, and $\Gamma_{L+\epsilon}$ is the branching factor of the dynamics over such states. This improves over the algorithm proposed in [1] in both $\epsilon$ and $L$ at the cost of an extra $\Gamma_{L+\epsilon}$ factor, which is small in most environments of interest. Furthermore, DisCo is the first algorithm that can return an $\epsilon/c_{\min}$-optimal policy for any cost-sensitive shortest-path problem defined on the $L$-reachable states with minimum cost $c_{\min}$. Finally, we report preliminary empirical results confirming our theoretical findings.

An Asymptotically Optimal Primal-Dual Incremental Algorithm for Contextual Linear Bandits

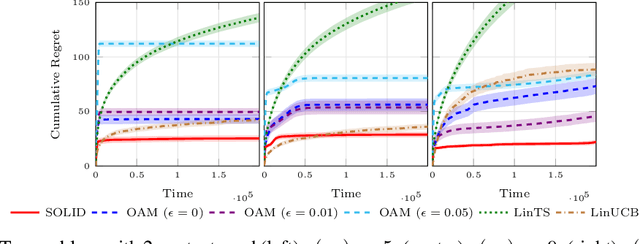
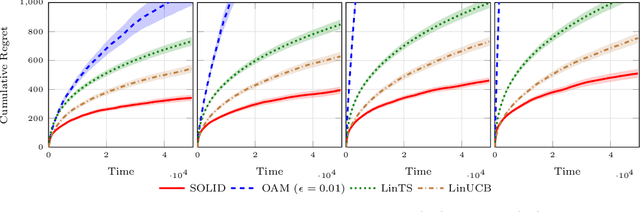
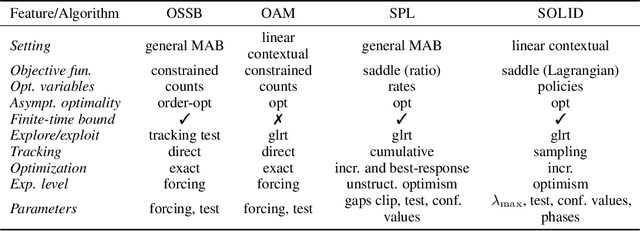
In the contextual linear bandit setting, algorithms built on the optimism principle fail to exploit the structure of the problem and have been shown to be asymptotically suboptimal. In this paper, we follow recent approaches of deriving asymptotically optimal algorithms from problem-dependent regret lower bounds and we introduce a novel algorithm improving over the state-of-the-art along multiple dimensions. We build on a reformulation of the lower bound, where context distribution and exploration policy are decoupled, and we obtain an algorithm robust to unbalanced context distributions. Then, using an incremental primal-dual approach to solve the Lagrangian relaxation of the lower bound, we obtain a scalable and computationally efficient algorithm. Finally, we remove forced exploration and build on confidence intervals of the optimization problem to encourage a minimum level of exploration that is better adapted to the problem structure. We demonstrate the asymptotic optimality of our algorithm, while providing both problem-dependent and worst-case finite-time regret guarantees. Our bounds scale with the logarithm of the number of arms, thus avoiding the linear dependence common in all related prior works. Notably, we establish minimax optimality for any learning horizon in the special case of non-contextual linear bandits. Finally, we verify that our algorithm obtains better empirical performance than state-of-the-art baselines.

Local Differentially Private Regret Minimization in Reinforcement Learning

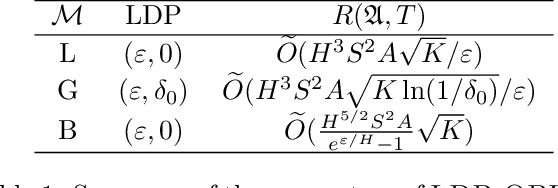
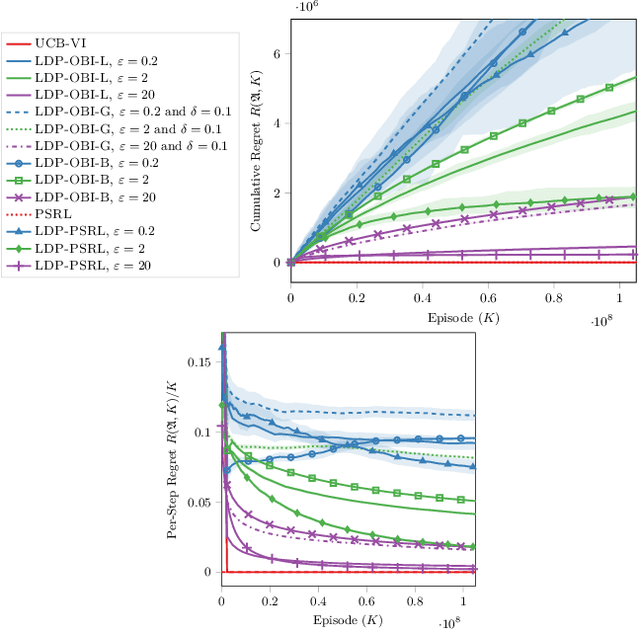
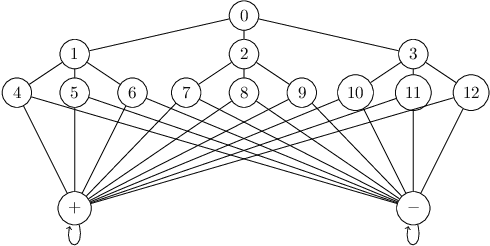
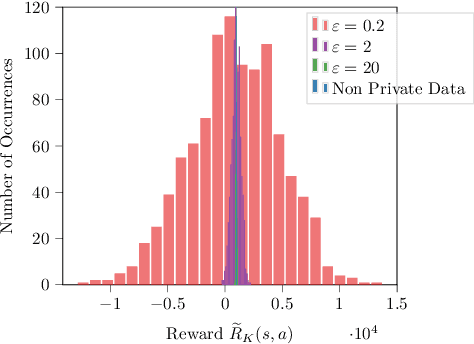
Reinforcement learning algorithms are widely used in domains where it is desirable to provide a personalized service. In these domains it is common that user data contains sensitive information that needs to be protected from third parties. Motivated by this, we study privacy in the context of finite-horizon Markov Decision Processes (MDPs) by requiring information to be obfuscated on the user side. We formulate this notion of privacy for RL by leveraging the local differential privacy (LDP) framework. We present an optimistic algorithm that simultaneously satisfies LDP requirements, and achieves sublinear regret. We also establish a lower bound for regret minimization in finite-horizon MDPs with LDP guarantees. These results show that while LDP is appealing in practical applications, the setting is inherently more complex. In particular, our results demonstrate that the cost of privacy is multiplicative when compared to non-private settings.

A Provably Efficient Sample Collection Strategy for Reinforcement Learning

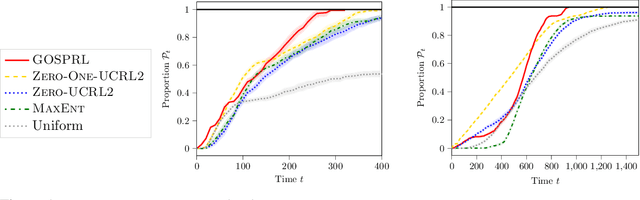
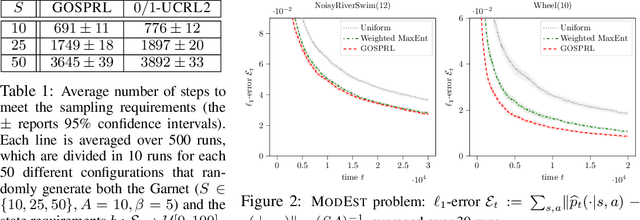
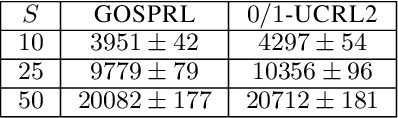
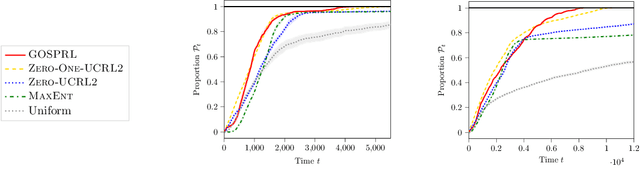
A common assumption in reinforcement learning (RL) is to have access to a generative model (i.e., a simulator of the environment), which allows to generate samples from any desired state-action pair. Nonetheless, in many settings a generative model may not be available and an adaptive exploration strategy is needed to efficiently collect samples from an unknown environment by direct interaction. In this paper, we study the scenario where an algorithm based on the generative model assumption defines the (possibly time-varying) amount of samples $b(s,a)$ required at each state-action pair $(s,a)$ and an exploration strategy has to learn how to generate $b(s,a)$ samples as fast as possible. Building on recent results for regret minimization in the stochastic shortest path (SSP) setting (Cohen et al., 2020; Tarbouriech et al., 2020), we derive an algorithm that requires $\tilde{O}( B D + D^{3/2} S^2 A)$ time steps to collect the $B = \sum_{s,a} b(s,a)$ desired samples, in any unknown and communicating MDP with $S$ states, $A$ actions and diameter $D$. Leveraging the generality of our strategy, we readily apply it to a variety of existing settings (e.g., model estimation, pure exploration in MDPs) for which we obtain improved sample-complexity guarantees, and to a set of new problems such as best-state identification and sparse reward discovery.

Improved Analysis of UCRL2 with Empirical Bernstein Inequality

We consider the problem of exploration-exploitation in communicating Markov Decision Processes. We provide an analysis of UCRL2 with Empirical Bernstein inequalities (UCRL2B). For any MDP with $S$ states, $A$ actions, $\Gamma \leq S$ next states and diameter $D$, the regret of UCRL2B is bounded as $\widetilde{O}(\sqrt{D\Gamma S A T})$.

A Kernel-Based Approach to Non-Stationary Reinforcement Learning in Metric Spaces

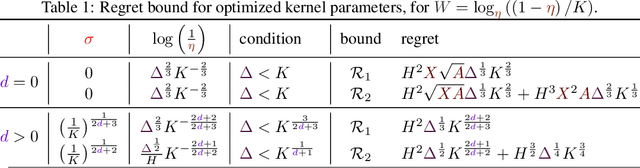
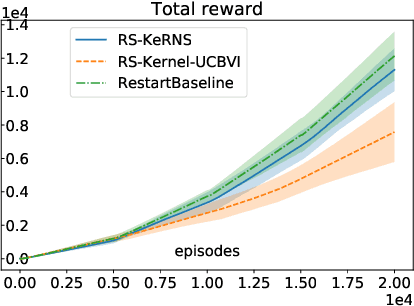
In this work, we propose KeRNS: an algorithm for episodic reinforcement learning in non-stationary Markov Decision Processes (MDPs) whose state-action set is endowed with a metric. Using a non-parametric model of the MDP built with time-dependent kernels, we prove a regret bound that scales with the covering dimension of the state-action space and the total variation of the MDP with time, which quantifies its level of non-stationarity. Our method generalizes previous approaches based on sliding windows and exponential discounting used to handle changing environments. We further propose a practical implementation of KeRNS, we analyze its regret and validate it experimentally.

Learning Adaptive Exploration Strategies in Dynamic Environments Through Informed Policy Regularization

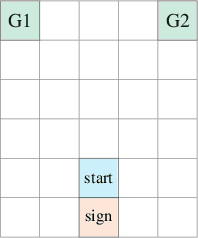
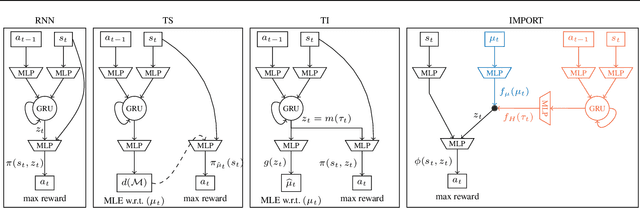
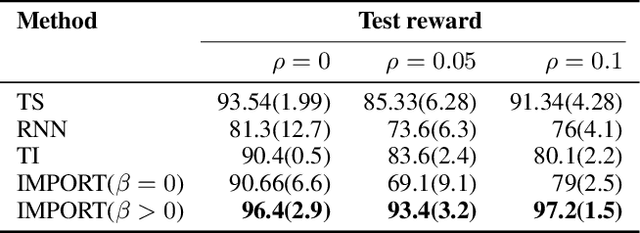
We study the problem of learning exploration-exploitation strategies that effectively adapt to dynamic environments, where the task may change over time. While RNN-based policies could in principle represent such strategies, in practice their training time is prohibitive and the learning process often converges to poor solutions. In this paper, we consider the case where the agent has access to a description of the task (e.g., a task id or task parameters) at training time, but not at test time. We propose a novel algorithm that regularizes the training of an RNN-based policy using informed policies trained to maximize the reward in each task. This dramatically reduces the sample complexity of training RNN-based policies, without losing their representational power. As a result, our method learns exploration strategies that efficiently balance between gathering information about the unknown and changing task and maximizing the reward over time. We test the performance of our algorithm in a variety of environments where tasks may vary within each episode.