QuACK: A Multipurpose Queuing Algorithm for Cooperative $k$-Armed Bandits

We study the cooperative stochastic $k$-armed bandit problem, where a network of $m$ agents collaborate to find the optimal action. In contrast to most prior work on this problem, which focuses on extending a specific algorithm to the multi-agent setting, we provide a black-box reduction that allows us to extend any single-agent bandit algorithm to the multi-agent setting. Under mild assumptions on the bandit environment, we prove that our reduction transfers the regret guarantees of the single-agent algorithm to the multi-agent setting. These guarantees are tight in subgaussian environments, in that using a near minimax optimal single-player algorithm is near minimax optimal in the multi-player setting up to an additive graph-dependent quantity. Our reduction and theoretical results are also general, and apply to many different bandit settings. By plugging in appropriate single-player algorithms, we can easily develop provably efficient algorithms for many multi-player settings such as heavy-tailed bandits, duelling bandits and bandits with local differential privacy, among others. Experimentally, our approach is competitive with or outperforms specialised multi-agent algorithms.

Sample-Efficiency in Multi-Batch Reinforcement Learning: The Need for Dimension-Dependent Adaptivity

We theoretically explore the relationship between sample-efficiency and adaptivity in reinforcement learning. An algorithm is sample-efficient if it uses a number of queries $n$ to the environment that is polynomial in the dimension $d$ of the problem. Adaptivity refers to the frequency at which queries are sent and feedback is processed to update the querying strategy. To investigate this interplay, we employ a learning framework that allows sending queries in $K$ batches, with feedback being processed and queries updated after each batch. This model encompasses the whole adaptivity spectrum, ranging from non-adaptive 'offline' ($K=1$) to fully adaptive ($K=n$) scenarios, and regimes in between. For the problems of policy evaluation and best-policy identification under $d$-dimensional linear function approximation, we establish $\Omega(\log \log d)$ lower bounds on the number of batches $K$ required for sample-efficient algorithms with $n = O(poly(d))$ queries. Our results show that just having adaptivity ($K>1$) does not necessarily guarantee sample-efficiency. Notably, the adaptivity-boundary for sample-efficiency is not between offline reinforcement learning ($K=1$), where sample-efficiency was known to not be possible, and adaptive settings. Instead, the boundary lies between different regimes of adaptivity and depends on the problem dimension.

Trading-Off Payments and Accuracy in Online Classification with Paid Stochastic Experts

We investigate online classification with paid stochastic experts. Here, before making their prediction, each expert must be paid. The amount that we pay each expert directly influences the accuracy of their prediction through some unknown Lipschitz "productivity" function. In each round, the learner must decide how much to pay each expert and then make a prediction. They incur a cost equal to a weighted sum of the prediction error and upfront payments for all experts. We introduce an online learning algorithm whose total cost after $T$ rounds exceeds that of a predictor which knows the productivity of all experts in advance by at most $\mathcal{O}(K^2(\log T)\sqrt{T})$ where $K$ is the number of experts. In order to achieve this result, we combine Lipschitz bandits and online classification with surrogate losses. These tools allow us to improve upon the bound of order $T^{2/3}$ one would obtain in the standard Lipschitz bandit setting. Our algorithm is empirically evaluated on synthetic data

Optimal Convergence Rate for Exact Policy Mirror Descent in Discounted Markov Decision Processes

The classical algorithms used in tabular reinforcement learning (Value Iteration and Policy Iteration) have been shown to converge linearly with a rate given by the discount factor $\gamma$ of a discounted Markov Decision Process. Recently, there has been an increased interest in the study of gradient based methods. In this work, we show that the dimension-free linear $\gamma$-rate of classical reinforcement learning algorithms can be achieved by a general family of unregularised Policy Mirror Descent (PMD) algorithms under an adaptive step-size. We also provide a matching worst-case lower-bound that demonstrates that the $\gamma$-rate is optimal for PMD methods. Our work offers a novel perspective on the convergence of PMD. We avoid the use of the performance difference lemma beyond establishing the monotonic improvement of the iterates, which leads to a simple analysis that may be of independent interest. We also extend our analysis to the inexact setting and establish the first dimension-free $\varepsilon$-optimal sample complexity for unregularised PMD under a generative model, improving upon the best-known result.

Delayed Feedback in Kernel Bandits

Black box optimisation of an unknown function from expensive and noisy evaluations is a ubiquitous problem in machine learning, academic research and industrial production. An abstraction of the problem can be formulated as a kernel based bandit problem (also known as Bayesian optimisation), where a learner aims at optimising a kernelized function through sequential noisy observations. The existing work predominantly assumes feedback is immediately available; an assumption which fails in many real world situations, including recommendation systems, clinical trials and hyperparameter tuning. We consider a kernel bandit problem under stochastically delayed feedback, and propose an algorithm with $\tilde{\mathcal{O}}(\sqrt{\Gamma_k(T)T}+\mathbb{E}[\tau])$ regret, where $T$ is the number of time steps, $\Gamma_k(T)$ is the maximum information gain of the kernel with $T$ observations, and $\tau$ is the delay random variable. This represents a significant improvement over the state of the art regret bound of $\tilde{\mathcal{O}}(\Gamma_k(T)\sqrt{T}+\mathbb{E}[\tau]\Gamma_k(T))$ reported in Verma et al. (2022). In particular, for very non-smooth kernels, the information gain grows almost linearly in time, trivializing the existing results. We also validate our theoretical results with simulations.

Delayed Feedback in Generalised Linear Bandits Revisited

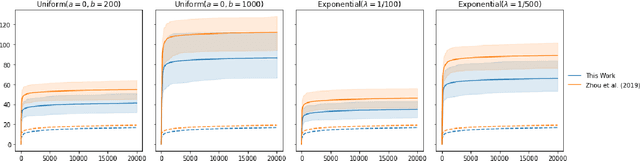
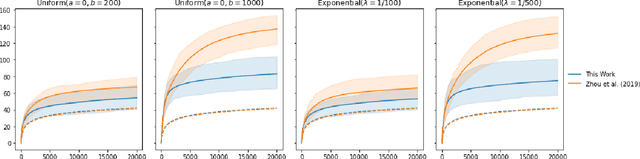
The stochastic generalised linear bandit is a well-understood model for sequential decision-making problems, with many algorithms achieving near-optimal regret guarantees under immediate feedback. However, in many real world settings, the requirement that the reward is observed immediately is not applicable. In this setting, standard algorithms are no longer theoretically understood. We study the phenomenon of delayed rewards in a theoretical manner by introducing a delay between selecting an action and receiving the reward. Subsequently, we show that an algorithm based on the optimistic principle improves on existing approaches for this setting by eliminating the need for prior knowledge of the delay distribution and relaxing assumptions on the decision set and the delays. This also leads to improving the regret guarantees from $ \widetilde O(\sqrt{dT}\sqrt{d + \mathbb{E}[\tau]})$ to $ \widetilde O(d\sqrt{T} + d^{3/2}\mathbb{E}[\tau])$, where $\mathbb{E}[\tau]$ denotes the expected delay, $d$ is the dimension and $T$ the time horizon and we have suppressed logarithmic terms. We verify our theoretical results through experiments on simulated data.

Bandit problems with fidelity rewards

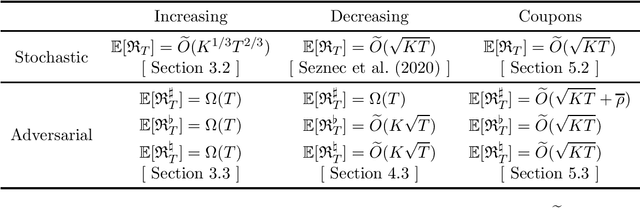
The fidelity bandits problem is a variant of the $K$-armed bandit problem in which the reward of each arm is augmented by a fidelity reward that provides the player with an additional payoff depending on how 'loyal' the player has been to that arm in the past. We propose two models for fidelity. In the loyalty-points model the amount of extra reward depends on the number of times the arm has previously been played. In the subscription model the additional reward depends on the current number of consecutive draws of the arm. We consider both stochastic and adversarial problems. Since single-arm strategies are not always optimal in stochastic problems, the notion of regret in the adversarial setting needs careful adjustment. We introduce three possible notions of regret and investigate which can be bounded sublinearly. We study in detail the special cases of increasing, decreasing and coupon (where the player gets an additional reward after every $m$ plays of an arm) fidelity rewards. For the models which do not necessarily enjoy sublinear regret, we provide a worst case lower bound. For those models which exhibit sublinear regret, we provide algorithms and bound their regret.

Delayed Feedback in Episodic Reinforcement Learning

There are many provably efficient algorithms for episodic reinforcement learning. However, these algorithms are built under the assumption that the sequences of states, actions and rewards associated with each episode arrive immediately, allowing policy updates after every interaction with the environment. This assumption is often unrealistic in practice, particularly in areas such as healthcare and online recommendation. In this paper, we study the impact of delayed feedback on several provably efficient algorithms for regret minimisation in episodic reinforcement learning. Firstly, we consider updating the policy as soon as new feedback becomes available. Using this updating scheme, we show that the regret increases by an additive term involving the number of states, actions, episode length and the expected delay. This additive term changes depending on the optimistic algorithm of choice. We also show that updating the policy less frequently can lead to an improved dependency of the regret on the delays.

Local Differentially Private Regret Minimization in Reinforcement Learning

Reinforcement learning algorithms are widely used in domains where it is desirable to provide a personalized service. In these domains it is common that user data contains sensitive information that needs to be protected from third parties. Motivated by this, we study privacy in the context of finite-horizon Markov Decision Processes (MDPs) by requiring information to be obfuscated on the user side. We formulate this notion of privacy for RL by leveraging the local differential privacy (LDP) framework. We present an optimistic algorithm that simultaneously satisfies LDP requirements, and achieves sublinear regret. We also establish a lower bound for regret minimization in finite-horizon MDPs with LDP guarantees. These results show that while LDP is appealing in practical applications, the setting is inherently more complex. In particular, our results demonstrate that the cost of privacy is multiplicative when compared to non-private settings.

A Unifying View of Optimism in Episodic Reinforcement Learning

The principle of optimism in the face of uncertainty underpins many theoretically successful reinforcement learning algorithms. In this paper we provide a general framework for designing, analyzing and implementing such algorithms in the episodic reinforcement learning problem. This framework is built upon Lagrangian duality, and demonstrates that every model-optimistic algorithm that constructs an optimistic MDP has an equivalent representation as a value-optimistic dynamic programming algorithm. Typically, it was thought that these two classes of algorithms were distinct, with model-optimistic algorithms benefiting from a cleaner probabilistic analysis while value-optimistic algorithms are easier to implement and thus more practical. With the framework developed in this paper, we show that it is possible to get the best of both worlds by providing a class of algorithms which have a computationally efficient dynamic-programming implementation and also a simple probabilistic analysis. Besides being able to capture many existing algorithms in the tabular setting, our framework can also address largescale problems under realizable function approximation, where it enables a simple model-based analysis of some recently proposed methods.