Scalable Representation Learning in Linear Contextual Bandits with Constant Regret Guarantees

We study the problem of representation learning in stochastic contextual linear bandits. While the primary concern in this domain is usually to find realizable representations (i.e., those that allow predicting the reward function at any context-action pair exactly), it has been recently shown that representations with certain spectral properties (called HLS) may be more effective for the exploration-exploitation task, enabling LinUCB to achieve constant (i.e., horizon-independent) regret. In this paper, we propose BanditSRL, a representation learning algorithm that combines a novel constrained optimization problem to learn a realizable representation with good spectral properties with a generalized likelihood ratio test to exploit the recovered representation and avoid excessive exploration. We prove that BanditSRL can be paired with any no-regret algorithm and achieve constant regret whenever an HLS representation is available. Furthermore, BanditSRL can be easily combined with deep neural networks and we show how regularizing towards HLS representations is beneficial in standard benchmarks.

Contextual bandits with concave rewards, and an application to fair ranking

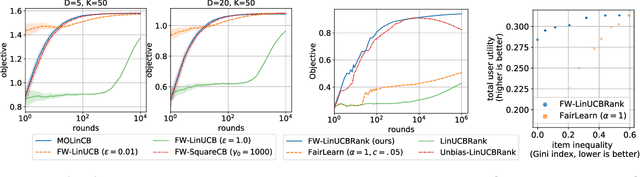
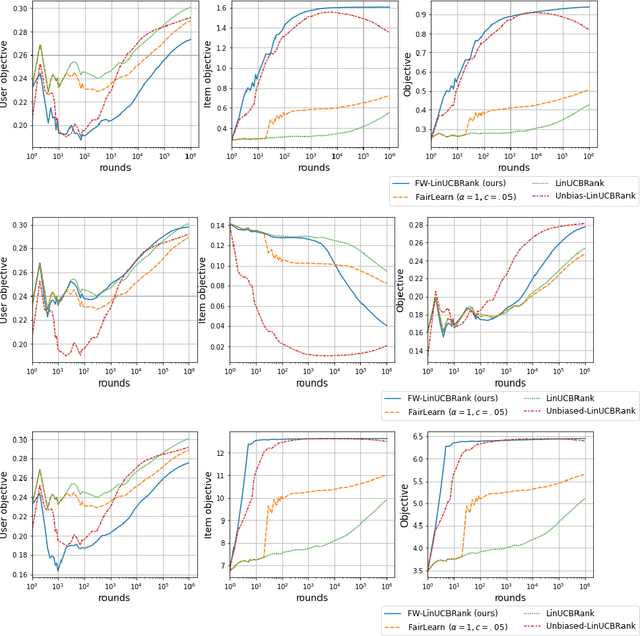
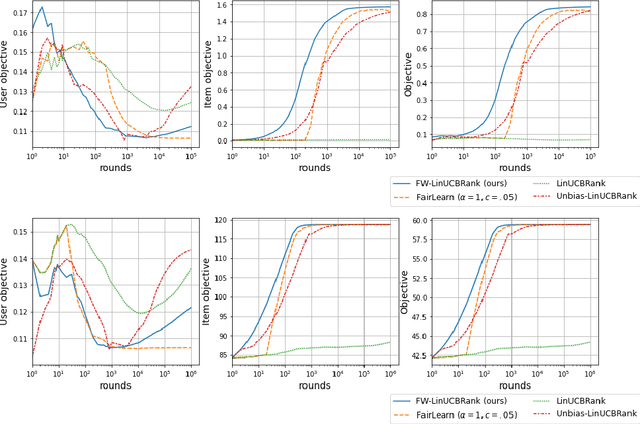
We consider Contextual Bandits with Concave Rewards (CBCR), a multi-objective bandit problem where the desired trade-off between the rewards is defined by a known concave objective function, and the reward vector depends on an observed stochastic context. We present the first algorithm with provably vanishing regret for CBCR without restrictions on the policy space, whereas prior works were restricted to finite policy spaces or tabular representations. Our solution is based on a geometric interpretation of CBCR algorithms as optimization algorithms over the convex set of expected rewards spanned by all stochastic policies. Building on Frank-Wolfe analyses in constrained convex optimization, we derive a novel reduction from the CBCR regret to the regret of a scalar-reward bandit problem. We illustrate how to apply the reduction off-the-shelf to obtain algorithms for CBCR with both linear and general reward functions, in the case of non-combinatorial actions. Motivated by fairness in recommendation, we describe a special case of CBCR with rankings and fairness-aware objectives, leading to the first algorithm with regret guarantees for contextual combinatorial bandits with fairness of exposure.

Reaching Goals is Hard: Settling the Sample Complexity of the Stochastic Shortest Path

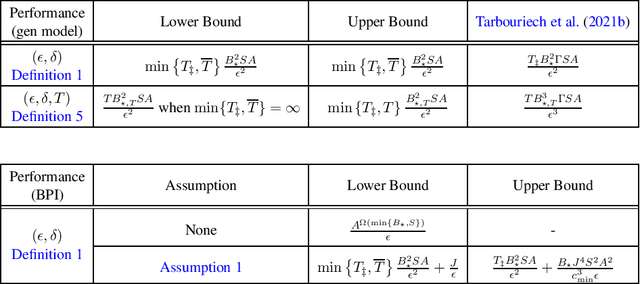
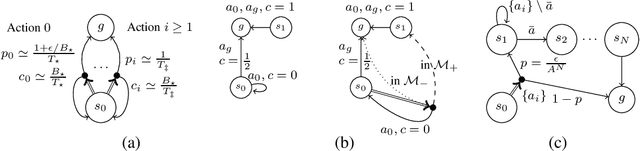
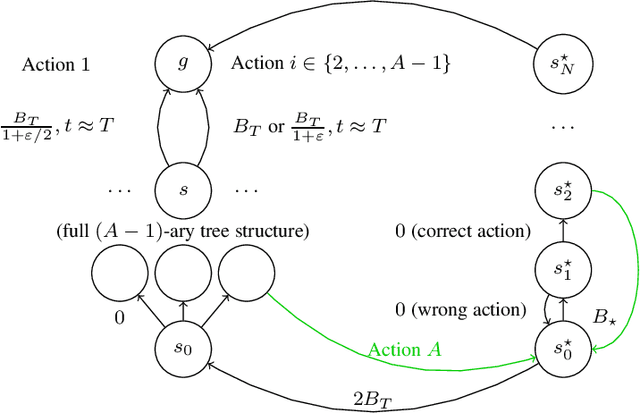
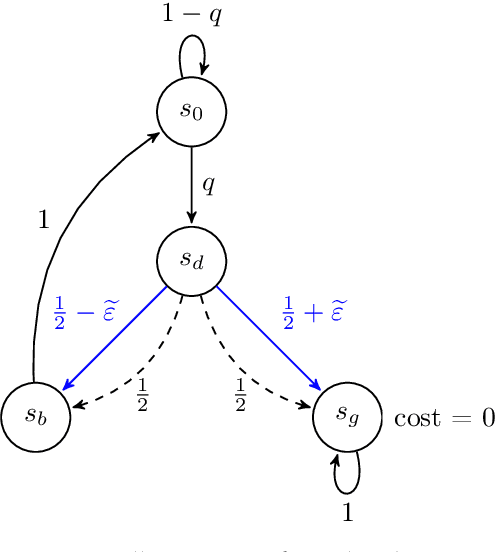
We study the sample complexity of learning an $\epsilon$-optimal policy in the Stochastic Shortest Path (SSP) problem. We first derive sample complexity bounds when the learner has access to a generative model. We show that there exists a worst-case SSP instance with $S$ states, $A$ actions, minimum cost $c_{\min}$, and maximum expected cost of the optimal policy over all states $B_{\star}$, where any algorithm requires at least $\Omega(SAB_{\star}^3/(c_{\min}\epsilon^2))$ samples to return an $\epsilon$-optimal policy with high probability. Surprisingly, this implies that whenever $c_{\min}=0$ an SSP problem may not be learnable, thus revealing that learning in SSPs is strictly harder than in the finite-horizon and discounted settings. We complement this result with lower bounds when prior knowledge of the hitting time of the optimal policy is available and when we restrict optimality by competing against policies with bounded hitting time. Finally, we design an algorithm with matching upper bounds in these cases. This settles the sample complexity of learning $\epsilon$-optimal polices in SSP with generative models. We also initiate the study of learning $\epsilon$-optimal policies without access to a generative model (i.e., the so-called best-policy identification problem), and show that sample-efficient learning is impossible in general. On the other hand, efficient learning can be made possible if we assume the agent can directly reach the goal state from any state by paying a fixed cost. We then establish the first upper and lower bounds under this assumption. Finally, using similar analytic tools, we prove that horizon-free regret is impossible in SSPs under general costs, resolving an open problem in (Tarbouriech et al., 2021c).

Top $K$ Ranking for Multi-Armed Bandit with Noisy Evaluations

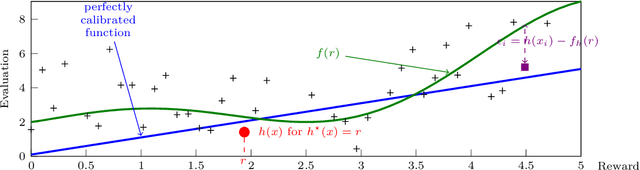
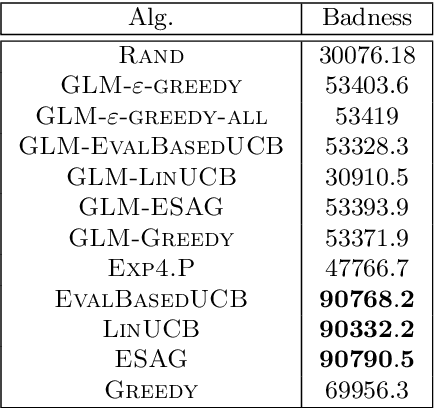
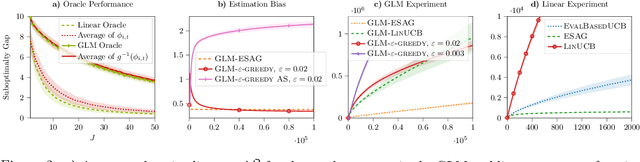
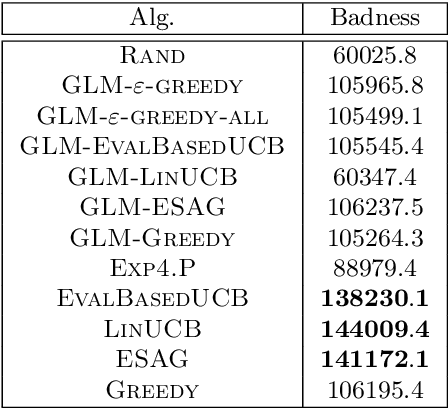
We consider a multi-armed bandit setting where, at the beginning of each round, the learner receives noisy independent, and possibly biased, \emph{evaluations} of the true reward of each arm and it selects $K$ arms with the objective of accumulating as much reward as possible over $T$ rounds. Under the assumption that at each round the true reward of each arm is drawn from a fixed distribution, we derive different algorithmic approaches and theoretical guarantees depending on how the evaluations are generated. First, we show a $\widetilde{O}(T^{2/3})$ regret in the general case when the observation functions are a genearalized linear function of the true rewards. On the other hand, we show that an improved $\widetilde{O}(\sqrt{T})$ regret can be derived when the observation functions are noisy linear functions of the true rewards. Finally, we report an empirical validation that confirms our theoretical findings, provides a thorough comparison to alternative approaches, and further supports the interest of this setting in practice.

Privacy Amplification via Shuffling for Linear Contextual Bandits

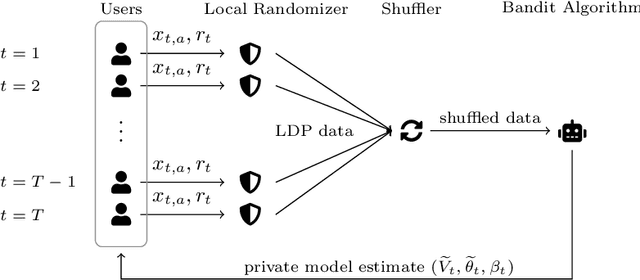
Contextual bandit algorithms are widely used in domains where it is desirable to provide a personalized service by leveraging contextual information, that may contain sensitive information that needs to be protected. Inspired by this scenario, we study the contextual linear bandit problem with differential privacy (DP) constraints. While the literature has focused on either centralized (joint DP) or local (local DP) privacy, we consider the shuffle model of privacy and we show that is possible to achieve a privacy/utility trade-off between JDP and LDP. By leveraging shuffling from privacy and batching from bandits, we present an algorithm with regret bound $\widetilde{\mathcal{O}}(T^{2/3}/\varepsilon^{1/3})$, while guaranteeing both central (joint) and local privacy. Our result shows that it is possible to obtain a trade-off between JDP and LDP by leveraging the shuffle model while preserving local privacy.

Differentially Private Exploration in Reinforcement Learning with Linear Representation

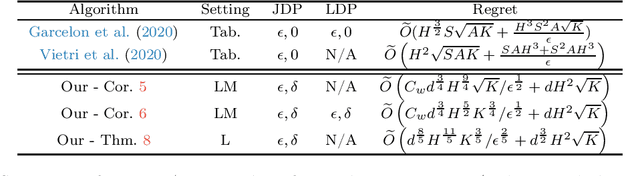
This paper studies privacy-preserving exploration in Markov Decision Processes (MDPs) with linear representation. We first consider the setting of linear-mixture MDPs (Ayoub et al., 2020) (a.k.a.\ model-based setting) and provide an unified framework for analyzing joint and local differential private (DP) exploration. Through this framework, we prove a $\widetilde{O}(K^{3/4}/\sqrt{\epsilon})$ regret bound for $(\epsilon,\delta)$-local DP exploration and a $\widetilde{O}(\sqrt{K/\epsilon})$ regret bound for $(\epsilon,\delta)$-joint DP. We further study privacy-preserving exploration in linear MDPs (Jin et al., 2020) (a.k.a.\ model-free setting) where we provide a $\widetilde{O}\left(K^{\frac{3}{5}}/\epsilon^{\frac{2}{5}}\right)$ regret bound for $(\epsilon,\delta)$-joint DP, with a novel algorithm based on low-switching. Finally, we provide insights into the issues of designing local DP algorithms in this model-free setting.

Adaptive Multi-Goal Exploration

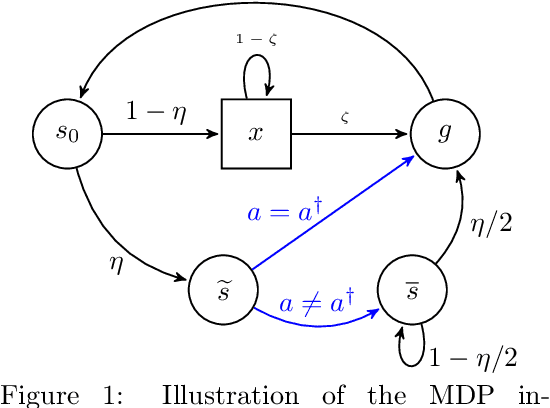
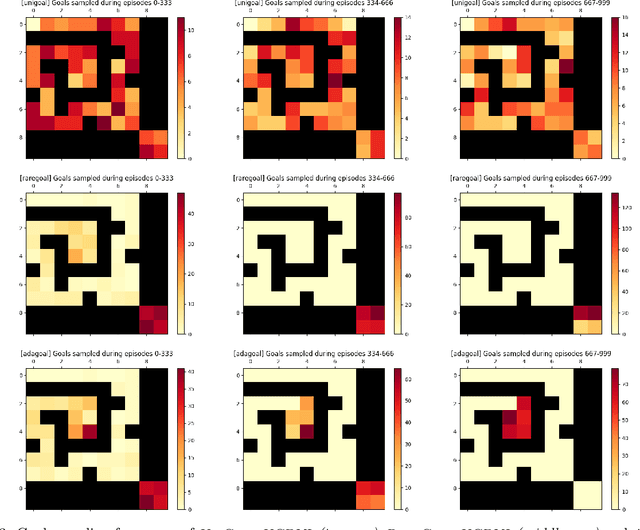
We introduce a generic strategy for provably efficient multi-goal exploration. It relies on AdaGoal, a novel goal selection scheme that is based on a simple constrained optimization problem, which adaptively targets goal states that are neither too difficult nor too easy to reach according to the agent's current knowledge. We show how AdaGoal can be used to tackle the objective of learning an $\epsilon$-optimal goal-conditioned policy for all the goal states that are reachable within $L$ steps in expectation from a reference state $s_0$ in a reward-free Markov decision process. In the tabular case with $S$ states and $A$ actions, our algorithm requires $\tilde{O}(L^3 S A \epsilon^{-2})$ exploration steps, which is nearly minimax optimal. We also readily instantiate AdaGoal in linear mixture Markov decision processes, which yields the first goal-oriented PAC guarantee with linear function approximation. Beyond its strong theoretical guarantees, AdaGoal is anchored in the high-level algorithmic structure of existing methods for goal-conditioned deep reinforcement learning.

Reinforcement Learning in Linear MDPs: Constant Regret and Representation Selection

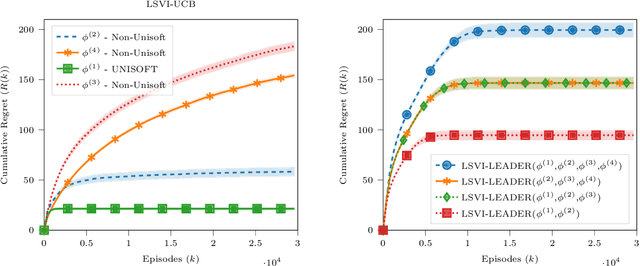
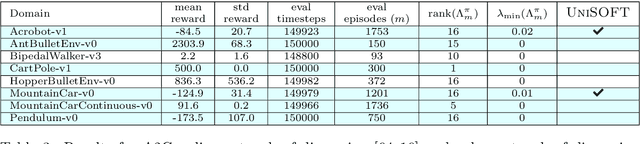
We study the role of the representation of state-action value functions in regret minimization in finite-horizon Markov Decision Processes (MDPs) with linear structure. We first derive a necessary condition on the representation, called universally spanning optimal features (UNISOFT), to achieve constant regret in any MDP with linear reward function. This result encompasses the well-known settings of low-rank MDPs and, more generally, zero inherent Bellman error (also known as the Bellman closure assumption). We then demonstrate that this condition is also sufficient for these classes of problems by deriving a constant regret bound for two optimistic algorithms (LSVI-UCB and ELEANOR). Finally, we propose an algorithm for representation selection and we prove that it achieves constant regret when one of the given representations, or a suitable combination of them, satisfies the UNISOFT condition.

A Fully Problem-Dependent Regret Lower Bound for Finite-Horizon MDPs

We derive a novel asymptotic problem-dependent lower-bound for regret minimization in finite-horizon tabular Markov Decision Processes (MDPs). While, similar to prior work (e.g., for ergodic MDPs), the lower-bound is the solution to an optimization problem, our derivation reveals the need for an additional constraint on the visitation distribution over state-action pairs that explicitly accounts for the dynamics of the MDP. We provide a characterization of our lower-bound through a series of examples illustrating how different MDPs may have significantly different complexity. 1) We first consider a "difficult" MDP instance, where the novel constraint based on the dynamics leads to a larger lower-bound (i.e., a larger regret) compared to the classical analysis. 2) We then show that our lower-bound recovers results previously derived for specific MDP instances. 3) Finally, we show that, in certain "simple" MDPs, the lower bound is considerably smaller than in the general case and it does not scale with the minimum action gap at all. We show that this last result is attainable (up to $poly(H)$ terms, where $H$ is the horizon) by providing a regret upper-bound based on policy gaps for an optimistic algorithm.

A Unified Framework for Conservative Exploration

We study bandits and reinforcement learning (RL) subject to a conservative constraint where the agent is asked to perform at least as well as a given baseline policy. This setting is particular relevant in real-world domains including digital marketing, healthcare, production, finance, etc. For multi-armed bandits, linear bandits and tabular RL, specialized algorithms and theoretical analyses were proposed in previous work. In this paper, we present a unified framework for conservative bandits and RL, in which our core technique is to calculate the necessary and sufficient budget obtained from running the baseline policy. For lower bounds, our framework gives a black-box reduction that turns a certain lower bound in the nonconservative setting into a new lower bound in the conservative setting. We strengthen the existing lower bound for conservative multi-armed bandits and obtain new lower bounds for conservative linear bandits, tabular RL and low-rank MDP. For upper bounds, our framework turns a certain nonconservative upper-confidence-bound (UCB) algorithm into a conservative algorithm with a simple analysis. For multi-armed bandits, linear bandits and tabular RL, our new upper bounds tighten or match existing ones with significantly simpler analyses. We also obtain a new upper bound for conservative low-rank MDP.