Differentiable Mapper For Topological Optimization Of Data Representation

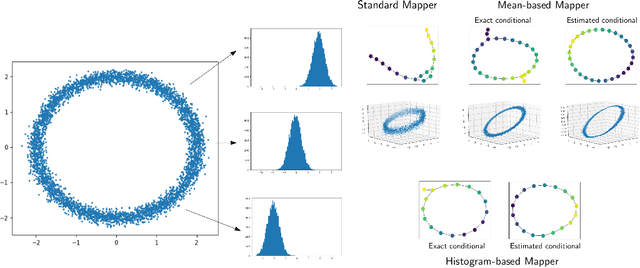
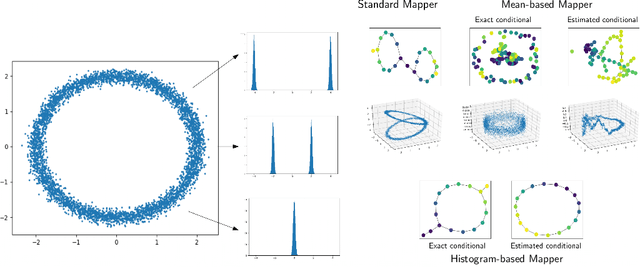
Unsupervised data representation and visualization using tools from topology is an active and growing field of Topological Data Analysis (TDA) and data science. Its most prominent line of work is based on the so-called Mapper graph, which is a combinatorial graph whose topological structures (connected components, branches, loops) are in correspondence with those of the data itself. While highly generic and applicable, its use has been hampered so far by the manual tuning of its many parameters-among these, a crucial one is the so-called filter: it is a continuous function whose variations on the data set are the main ingredient for both building the Mapper representation and assessing the presence and sizes of its topological structures. However, while a few parameter tuning methods have already been investigated for the other Mapper parameters (i.e., resolution, gain, clustering), there is currently no method for tuning the filter itself. In this work, we build on a recently proposed optimization framework incorporating topology to provide the first filter optimization scheme for Mapper graphs. In order to achieve this, we propose a relaxed and more general version of the Mapper graph, whose convergence properties are investigated. Finally, we demonstrate the usefulness of our approach by optimizing Mapper graph representations on several datasets, and showcasing the superiority of the optimized representation over arbitrary ones.

Weighted least-squares approximation with determinantal point processes and generalized volume sampling

We consider the problem of approximating a function from $L^2$ by an element of a given $m$-dimensional space $V_m$, associated with some feature map $\varphi$, using evaluations of the function at random points $x_1,\dots,x_n$. After recalling some results on optimal weighted least-squares using independent and identically distributed points, we consider weighted least-squares using projection determinantal point processes (DPP) or volume sampling. These distributions introduce dependence between the points that promotes diversity in the selected features $\varphi(x_i)$. We first provide a generalized version of volume-rescaled sampling yielding quasi-optimality results in expectation with a number of samples $n = O(m\log(m))$, that means that the expected $L^2$ error is bounded by a constant times the best approximation error in $L^2$. Also, further assuming that the function is in some normed vector space $H$ continuously embedded in $L^2$, we further prove that the approximation is almost surely bounded by the best approximation error measured in the $H$-norm. This includes the cases of functions from $L^\infty$ or reproducing kernel Hilbert spaces. Finally, we present an alternative strategy consisting in using independent repetitions of projection DPP (or volume sampling), yielding similar error bounds as with i.i.d. or volume sampling, but in practice with a much lower number of samples. Numerical experiments illustrate the performance of the different strategies.

Kernel-Based Testing for Single-Cell Differential Analysis

Single-cell technologies have provided valuable insights into the distribution of molecular features, such as gene expression and epigenomic modifications. However, comparing these complex distributions in a controlled and powerful manner poses methodological challenges. Here we propose to benefit from the kernel-testing framework to compare the complex cell-wise distributions of molecular features in a non-linear manner based on their kernel embedding. Our framework not only allows for feature-wise analyses but also enables global comparisons of transcriptomes or epigenomes, considering their intricate dependencies. By using a classifier to discriminate cells based on the variability of their embedding, our method uncovers heterogeneities in cell populations that would otherwise go undetected. We show that kernel testing overcomes the limitations of differential analysis methods dedicated to single-cell. Kernel testing is applied to investigate the reversion process of differentiating cells, successfully identifying cells in transition between reversion and differentiation stages. Additionally, we analyze single-cell ChIP-Seq data and identify a subpopulation of untreated breast cancer cells that exhibit an epigenomic profile similar to persister cells.

Topological phase estimation method for reparameterized periodic functions

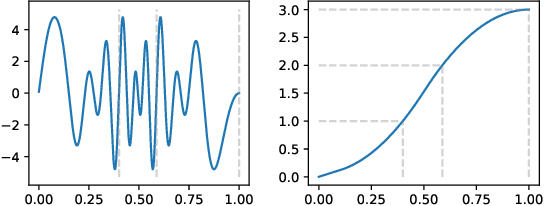
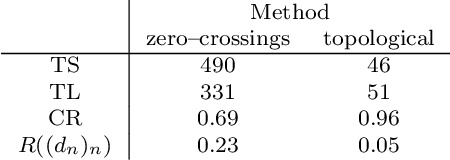
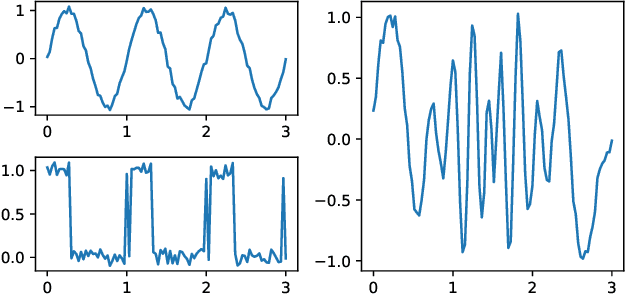
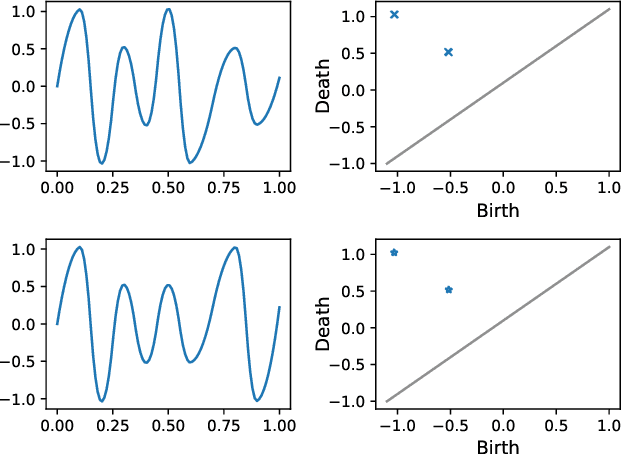
We consider a signal composed of several periods of a periodic function, of which we observe a noisy reparametrisation. The phase estimation problem consists of finding that reparametrisation, and, in particular, the number of observed periods. Existing methods are well-suited to the setting where the periodic function is known, or at least, simple. We consider the case when it is unknown and we propose an estimation method based on the shape of the signal. We use the persistent homology of sublevel sets of the signal to capture the temporal structure of its local extrema. We infer the number of periods in the signal by counting points in the persistence diagram and their multiplicities. Using the estimated number of periods, we construct an estimator of the reparametrisation. It is based on counting the number of sufficiently prominent local minima in the signal. This work is motivated by a vehicle positioning problem, on which we evaluated the proposed method.

Learning with tree tensor networks: complexity estimates and model selection

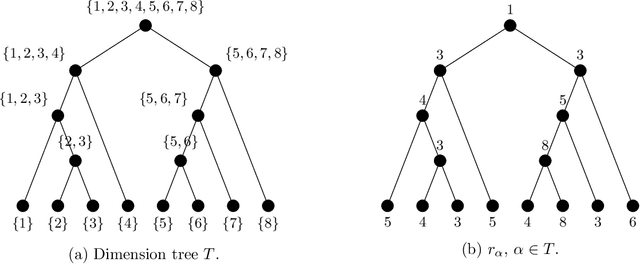
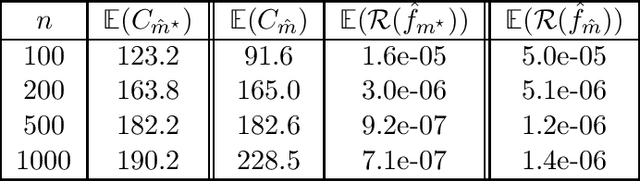
In this paper, we propose and analyze a model selection method for tree tensor networks in an empirical risk minimization framework. Tree tensor networks, or tree-based tensor formats, are prominent model classes for the approximation of high-dimensional functions in numerical analysis and data science. They correspond to sum-product neural networks with a sparse connectivity associated with a dimension partition tree $T$, widths given by a tuple $r$ of tensor ranks, and multilinear activation functions (or units). The approximation power of these model classes has been proved to be near-optimal for classical smoothness classes. However, in an empirical risk minimization framework with a limited number of observations, the dimension tree $T$ and ranks $r$ should be selected carefully to balance estimation and approximation errors. In this paper, we propose a complexity-based model selection strategy \`a la Barron, Birg\'e, Massart. Given a family of model classes, with different trees, ranks and tensor product feature spaces, a model is selected by minimizing a penalized empirical risk, with a penalty depending on the complexity of the model class. After deriving bounds of the metric entropy of tree tensor networks with bounded parameters, we deduce a form of the penalty from bounds on suprema of empirical processes. This choice of penalty yields a risk bound for the predictor associated with the selected model. For classical smoothness spaces, we show that the proposed strategy is minimax optimal in a least-squares setting. In practice, the amplitude of the penalty is calibrated with a slope heuristics method. Numerical experiments in a least-squares regression setting illustrate the performance of the strategy for the approximation of multivariate functions and univariate functions identified with tensors by tensorization (quantization).

Approximation of Reeb spaces with Mappers and Applications to Stochastic Filters

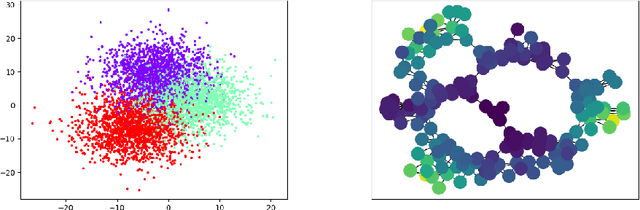
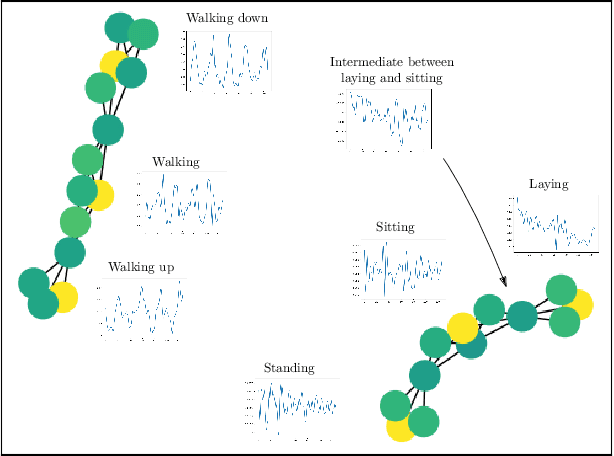
Reeb spaces, as well as their discretized versions called Mappers, are common descriptors used in Topological Data Analysis, with plenty of applications in various fields of science, such as computational biology and data visualization, among others. The stability and quantification of the rate of convergence of the Mapper to the Reeb space has been studied a lot in recent works~\cite{Brown2019, Carriere2018a, Carriere2018, Munch2016}, focusing on the case where a scalar-valued filter is used for the computation of Mapper. On the other hand, much less is known in the multivariate case, where the domain of the filter is in $\mathbb R^d$ instead of $\mathbb R$. The only available result in this setting~\cite{Munch2016} only works for topological spaces and cannot be used as is for finite metric spaces representing data, such as point clouds and distance matrices. In this article, we present an approximation result for the Reeb space in the multivariate case using a Mapper-based estimator, which is a slight modification of the usual Mapper construction. Moreover, our approximation is stated with respect to a pseudometric that is an extension of the usual {\em interleaving distance} between persistence modules~\cite{Chazal2016}. Finally, we apply our results to the case where the filter function used to compute the Mapper is estimated from the data. We provide applications of this setting in statistics and machine learning and probability for different kinds of target filters, as well as numerical experiments that demonstrate the relevance of our approach.

An introduction to Topological Data Analysis: fundamental and practical aspects for data scientists

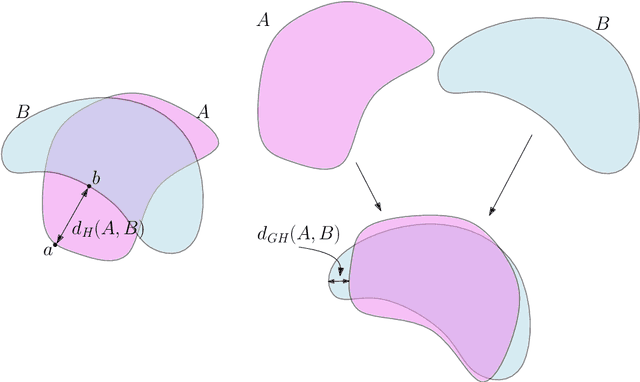
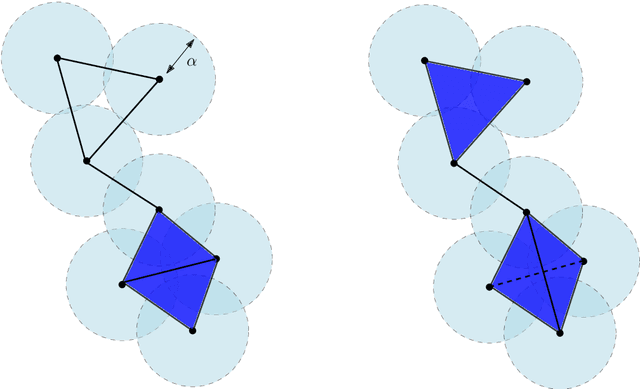
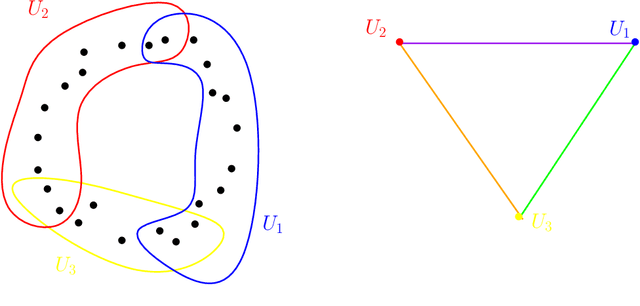
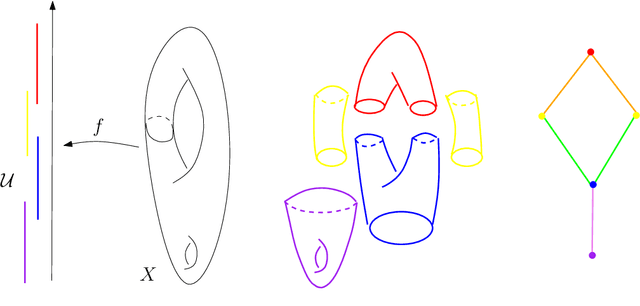
Topological Data Analysis (tda) is a recent and fast growing eld providing a set of new topological and geometric tools to infer relevant features for possibly complex data. This paper is a brief introduction, through a few selected topics, to basic fundamental and practical aspects of tda for non experts. 1 Introduction and motivation Topological Data Analysis (tda) is a recent eld that emerged from various works in applied (algebraic) topology and computational geometry during the rst decade of the century. Although one can trace back geometric approaches for data analysis quite far in the past, tda really started as a eld with the pioneering works of Edelsbrunner et al. (2002) and Zomorodian and Carlsson (2005) in persistent homology and was popularized in a landmark paper in 2009 Carlsson (2009). tda is mainly motivated by the idea that topology and geometry provide a powerful approach to infer robust qualitative, and sometimes quantitative, information about the structure of data-see, e.g. Chazal (2017). tda aims at providing well-founded mathematical, statistical and algorithmic methods to infer, analyze and exploit the complex topological and geometric structures underlying data that are often represented as point clouds in Euclidean or more general metric spaces. During the last few years, a considerable eort has been made to provide robust and ecient data structures and algorithms for tda that are now implemented and available and easy to use through standard libraries such as the Gudhi library (C++ and Python) Maria et al. (2014) and its R software interface Fasy et al. (2014a). Although it is still rapidly evolving, tda now provides a set of mature and ecient tools that can be used in combination or complementary to other data sciences tools. The tdapipeline. tda has recently known developments in various directions and application elds. There now exist a large variety of methods inspired by topological and geometric approaches. Providing a complete overview of all these existing approaches is beyond the scope of this introductory survey. However, most of them rely on the following basic and standard pipeline that will serve as the backbone of this paper: 1. The input is assumed to be a nite set of points coming with a notion of distance-or similarity between them. This distance can be induced by the metric in the ambient space (e.g. the Euclidean metric when the data are embedded in R d) or come as an intrinsic metric dened by a pairwise distance matrix. The denition of the metric on the data is usually given as an input or guided by the application. It is however important to notice that the choice of the metric may be critical to reveal interesting topological and geometric features of the data.

Data driven estimation of Laplace-Beltrami operator

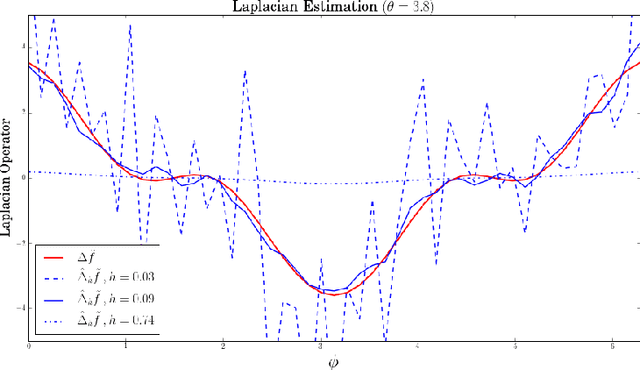
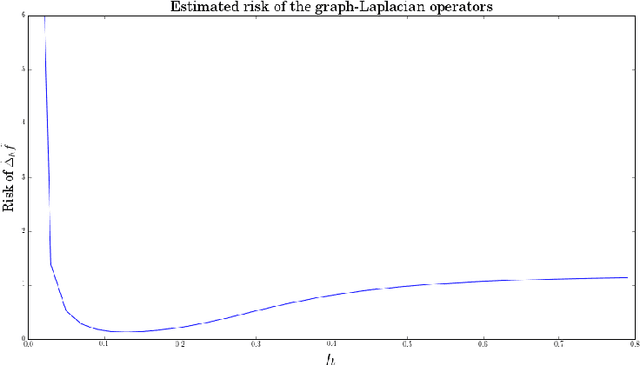
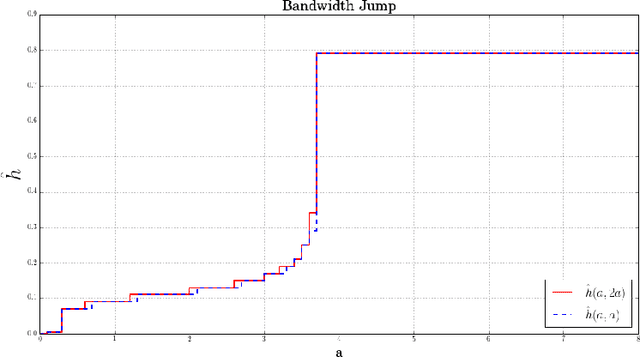
Approximations of Laplace-Beltrami operators on manifolds through graph Lapla-cians have become popular tools in data analysis and machine learning. These discretized operators usually depend on bandwidth parameters whose tuning remains a theoretical and practical problem. In this paper, we address this problem for the unnormalized graph Laplacian by establishing an oracle inequality that opens the door to a well-founded data-driven procedure for the bandwidth selection. Our approach relies on recent results by Lacour and Massart [LM15] on the so-called Lepski's method.

Sparse Bayesian Unsupervised Learning

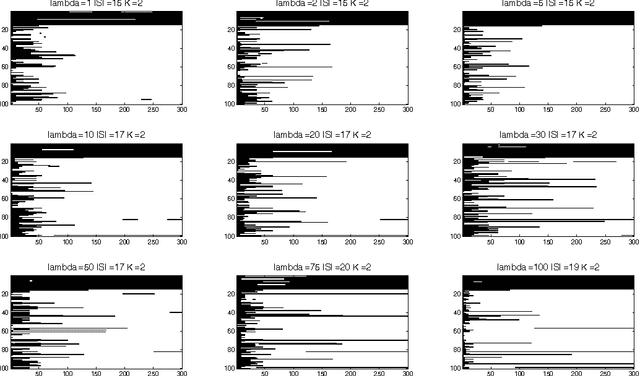
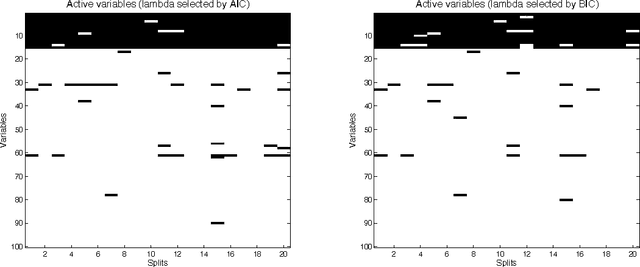
This paper is about variable selection, clustering and estimation in an unsupervised high-dimensional setting. Our approach is based on fitting constrained Gaussian mixture models, where we learn the number of clusters $K$ and the set of relevant variables $S$ using a generalized Bayesian posterior with a sparsity inducing prior. We prove a sparsity oracle inequality which shows that this procedure selects the optimal parameters $K$ and $S$. This procedure is implemented using a Metropolis-Hastings algorithm, based on a clustering-oriented greedy proposal, which makes the convergence to the posterior very fast.

Optimal rates of convergence for persistence diagrams in Topological Data Analysis

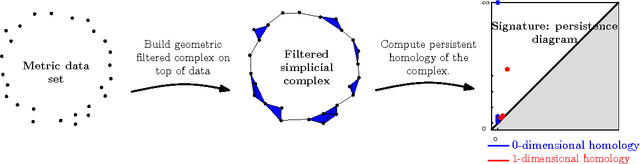
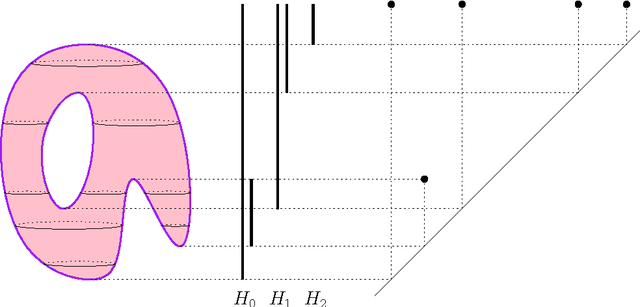
Computational topology has recently known an important development toward data analysis, giving birth to the field of topological data analysis. Topological persistence, or persistent homology, appears as a fundamental tool in this field. In this paper, we study topological persistence in general metric spaces, with a statistical approach. We show that the use of persistent homology can be naturally considered in general statistical frameworks and persistence diagrams can be used as statistics with interesting convergence properties. Some numerical experiments are performed in various contexts to illustrate our results.