Improving Content Retrievability in Search with Controllable Query Generation

An important goal of online platforms is to enable content discovery, i.e. allow users to find a catalog entity they were not familiar with. A pre-requisite to discover an entity, e.g. a book, with a search engine is that the entity is retrievable, i.e. there are queries for which the system will surface such entity in the top results. However, machine-learned search engines have a high retrievability bias, where the majority of the queries return the same entities. This happens partly due to the predominance of narrow intent queries, where users create queries using the title of an already known entity, e.g. in book search 'harry potter'. The amount of broad queries where users want to discover new entities, e.g. in music search 'chill lyrical electronica with an atmospheric feeling to it', and have a higher tolerance to what they might find, is small in comparison. We focus here on two factors that have a negative impact on the retrievability of the entities (I) the training data used for dense retrieval models and (II) the distribution of narrow and broad intent queries issued in the system. We propose CtrlQGen, a method that generates queries for a chosen underlying intent-narrow or broad. We can use CtrlQGen to improve factor (I) by generating training data for dense retrieval models comprised of diverse synthetic queries. CtrlQGen can also be used to deal with factor (II) by suggesting queries with broader intents to users. Our results on datasets from the domains of music, podcasts, and books reveal that we can significantly decrease the retrievability bias of a dense retrieval model when using CtrlQGen. First, by using the generated queries as training data for dense models we make 9% of the entities retrievable (go from zero to non-zero retrievability). Second, by suggesting broader queries to users, we can make 12% of the entities retrievable in the best case.

On Multi-Armed Bandit Designs for Phase I Clinical Trials

We study the problem of finding the optimal dosage in a phase I clinical trial through the multi-armed bandit lens. We advocate the use of the Thompson Sampling principle, a flexible algorithm that can accommodate different types of monotonicity assumptions on the toxicity and efficacy of the doses. For the simplest version of Thompson Sampling, based on a uniform prior distribution for each dose, we provide finite-time upper bounds on the number of sub-optimal dose selections, which is unprecedented for dose finding algorithms. Through a large simulation study, we then show that Thompson Sampling based on more sophisticated prior distributions outperform state-of-the-art dose identification algorithms in different types of phase I clinical trials.

Pure-Exploration for Infinite-Armed Bandits with General Arm Reservoirs

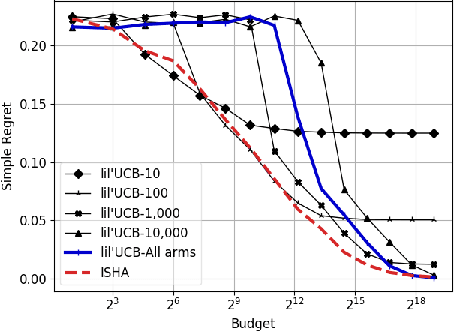
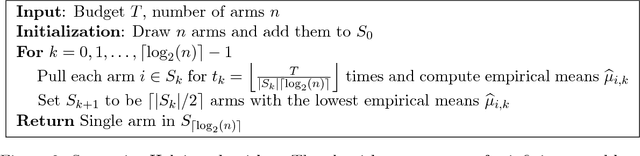
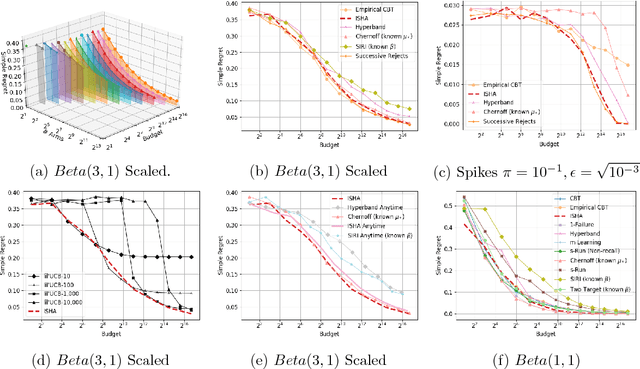
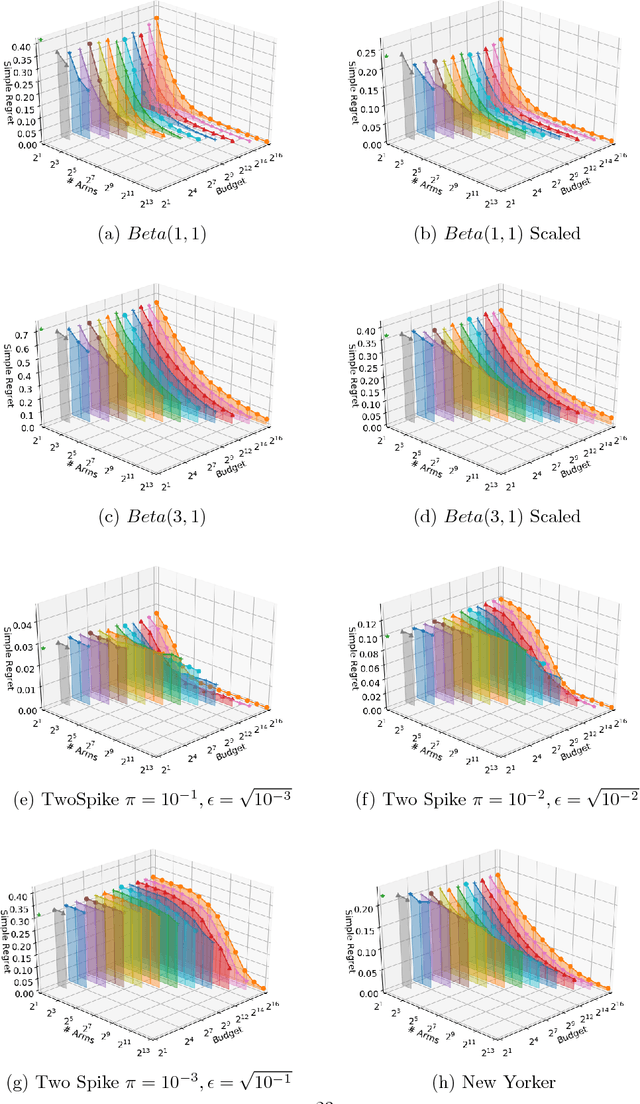
This paper considers a multi-armed bandit game where the number of arms is much larger than the maximum budget and is effectively infinite. We characterize necessary and sufficient conditions on the total budget for an algorithm to return an {\epsilon}-good arm with probability at least 1 - {\delta}. In such situations, the sample complexity depends on {\epsilon}, {\delta} and the so-called reservoir distribution {\nu} from which the means of the arms are drawn iid. While a substantial literature has developed around analyzing specific cases of {\nu} such as the beta distribution, our analysis makes no assumption about the form of {\nu}. Our algorithm is based on successive halving with the surprising exception that arms start to be discarded after just a single pull, requiring an analysis that goes beyond concentration alone. The provable correctness of this algorithm also provides an explanation for the empirical observation that the most aggressive bracket of the Hyperband algorithm of Li et al. (2017) for hyperparameter tuning is almost always best.

Adaptively Pruning Features for Boosted Decision Trees

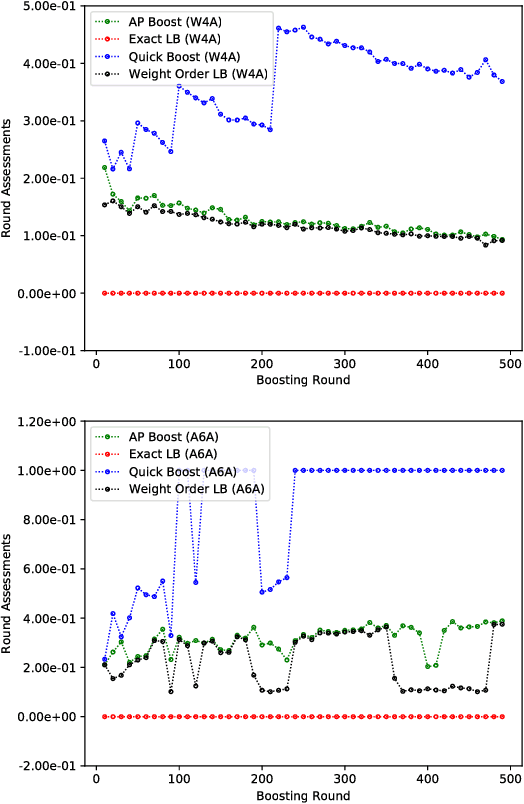
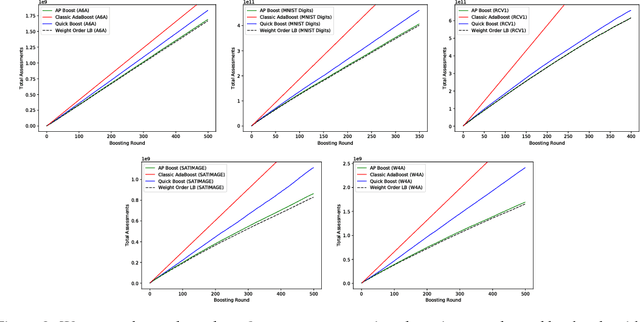
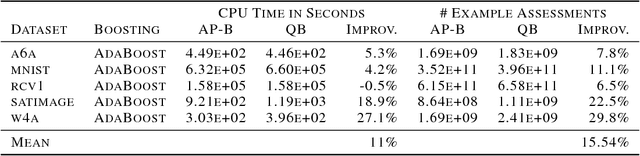
Boosted decision trees enjoy popularity in a variety of applications; however, for large-scale datasets, the cost of training a decision tree in each round can be prohibitively expensive. Inspired by ideas from the multi-arm bandit literature, we develop a highly efficient algorithm for computing exact greedy-optimal decision trees, outperforming the state-of-the-art Quick Boost method. We further develop a framework for deriving lower bounds on the problem that applies to a wide family of conceivable algorithms for the task (including our algorithm and Quick Boost), and we demonstrate empirically on a wide variety of data sets that our algorithm is near-optimal within this family of algorithms. We also derive a lower bound applicable to any algorithm solving the task, and we demonstrate that our algorithm empirically achieves performance close to this best-achievable lower bound.

Pure Exploration in Infinitely-Armed Bandit Models with Fixed-Confidence

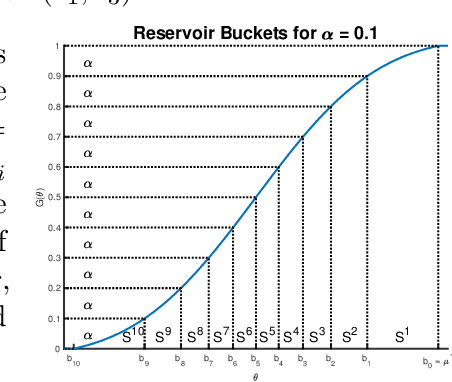
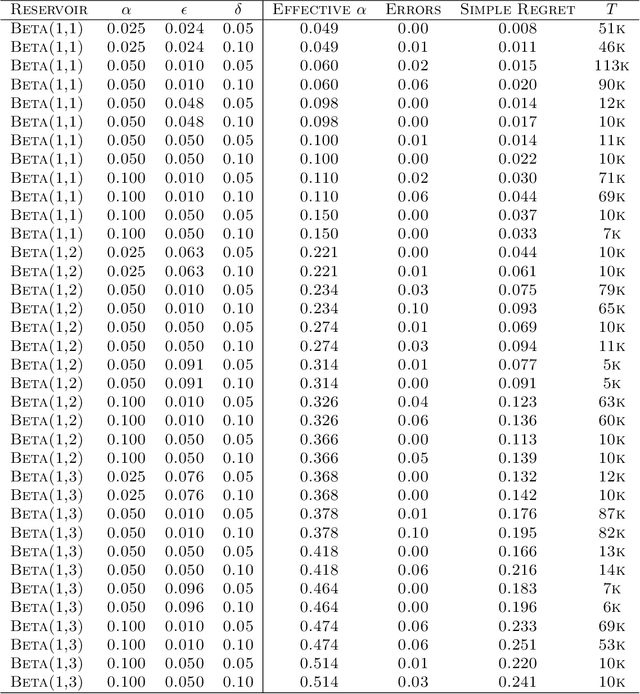
We consider the problem of near-optimal arm identification in the fixed confidence setting of the infinitely armed bandit problem when nothing is known about the arm reservoir distribution. We (1) introduce a PAC-like framework within which to derive and cast results; (2) derive a sample complexity lower bound for near-optimal arm identification; (3) propose an algorithm that identifies a nearly-optimal arm with high probability and derive an upper bound on its sample complexity which is within a log factor of our lower bound; and (4) discuss whether our log^2(1/delta) dependence is inescapable for "two-phase" (select arms first, identify the best later) algorithms in the infinite setting. This work permits the application of bandit models to a broader class of problems where fewer assumptions hold.