One Decade of Universal Artificial Intelligence

The first decade of this century has seen the nascency of the first mathematical theory of general artificial intelligence. This theory of Universal Artificial Intelligence (UAI) has made significant contributions to many theoretical, philosophical, and practical AI questions. In a series of papers culminating in book (Hutter, 2005), an exciting sound and complete mathematical model for a super intelligent agent (AIXI) has been developed and rigorously analyzed. While nowadays most AI researchers avoid discussing intelligence, the award-winning PhD thesis (Legg, 2008) provided the philosophical embedding and investigated the UAI-based universal measure of rational intelligence, which is formal, objective and non-anthropocentric. Recently, effective approximations of AIXI have been derived and experimentally investigated in JAIR paper (Veness et al. 2011). This practical breakthrough has resulted in some impressive applications, finally muting earlier critique that UAI is only a theory. For the first time, without providing any domain knowledge, the same agent is able to self-adapt to a diverse range of interactive environments. For instance, AIXI is able to learn from scratch to play TicTacToe, Pacman, Kuhn Poker, and other games by trial and error, without even providing the rules of the games. These achievements give new hope that the grand goal of Artificial General Intelligence is not elusive. This article provides an informal overview of UAI in context. It attempts to gently introduce a very theoretical, formal, and mathematical subject, and discusses philosophical and technical ingredients, traits of intelligence, some social questions, and the past and future of UAI.

PAC Bounds for Discounted MDPs

We study upper and lower bounds on the sample-complexity of learning near-optimal behaviour in finite-state discounted Markov Decision Processes (MDPs). For the upper bound we make the assumption that each action leads to at most two possible next-states and prove a new bound for a UCRL-style algorithm on the number of time-steps when it is not Probably Approximately Correct (PAC). The new lower bound strengthens previous work by being both more general (it applies to all policies) and tighter. The upper and lower bounds match up to logarithmic factors.

A Bayesian View of the Poisson-Dirichlet Process

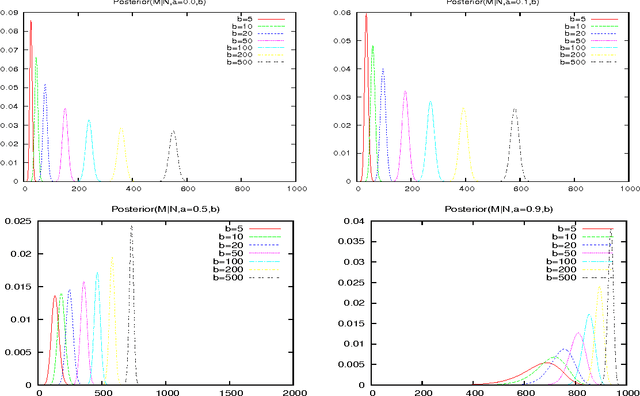
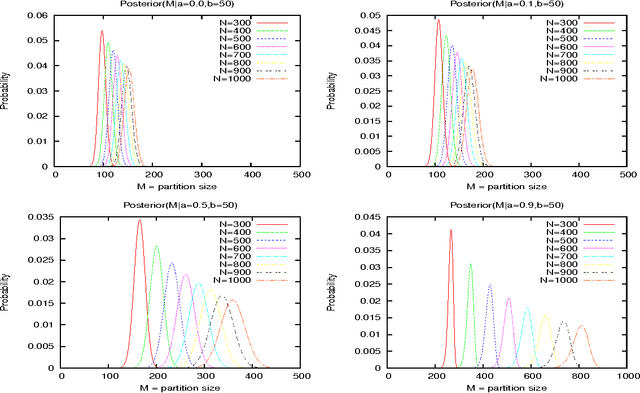
The two parameter Poisson-Dirichlet Process (PDP), a generalisation of the Dirichlet Process, is increasingly being used for probabilistic modelling in discrete areas such as language technology, bioinformatics, and image analysis. There is a rich literature about the PDP and its derivative distributions such as the Chinese Restaurant Process (CRP). This article reviews some of the basic theory and then the major results needed for Bayesian modelling of discrete problems including details of priors, posteriors and computation. The PDP allows one to build distributions over countable partitions. The PDP has two other remarkable properties: first it is partially conjugate to itself, which allows one to build hierarchies of PDPs, and second using a marginalised relative the CRP, one gets fragmentation and clustering properties that lets one layer partitions to build trees. This article presents the basic theory for understanding the notion of partitions and distributions over them, the PDP and the CRP, and the important properties of conjugacy, fragmentation and clustering, as well as some key related properties such as consistency and convergence. This article also presents a Bayesian interpretation of the Poisson-Dirichlet process based on an improper and infinite dimensional Dirichlet distribution. This means we can understand the process as just another Dirichlet and thus all its sampling properties emerge naturally. The theory of PDPs is usually presented for continuous distributions (more generally referred to as non-atomic distributions), however, when applied to discrete distributions its remarkable conjugacy property emerges. This context and basic results are also presented, as well as techniques for computing the second order Stirling numbers that occur in the posteriors for discrete distributions.

3D Model Assisted Image Segmentation

The problem of segmenting a given image into coherent regions is important in Computer Vision and many industrial applications require segmenting a known object into its components. Examples include identifying individual parts of a component for process control work in a manufacturing plant and identifying parts of a car from a photo for automatic damage detection. Unfortunately most of an object's parts of interest in such applications share the same pixel characteristics, having similar colour and texture. This makes segmenting the object into its components a non-trivial task for conventional image segmentation algorithms. In this paper, we propose a "Model Assisted Segmentation" method to tackle this problem. A 3D model of the object is registered over the given image by optimising a novel gradient based loss function. This registration obtains the full 3D pose from an image of the object. The image can have an arbitrary view of the object and is not limited to a particular set of views. The segmentation is subsequently performed using a level-set based method, using the projected contours of the registered 3D model as initialisation curves. The method is fully automatic and requires no user interaction. Also, the system does not require any prior training. We present our results on photographs of a real car.

Adaptive Context Tree Weighting

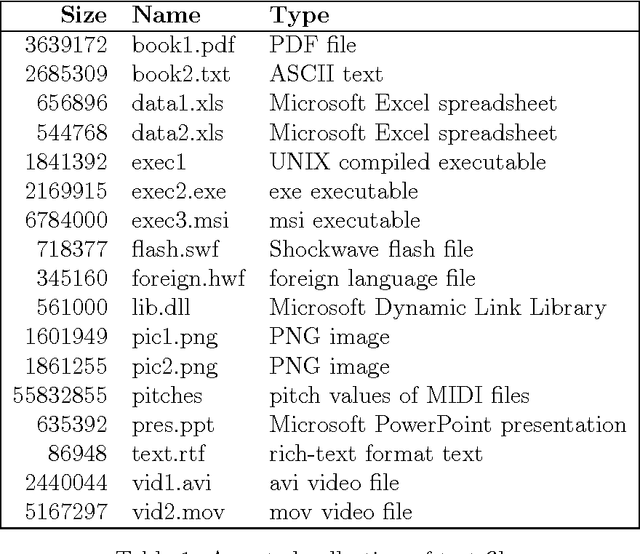
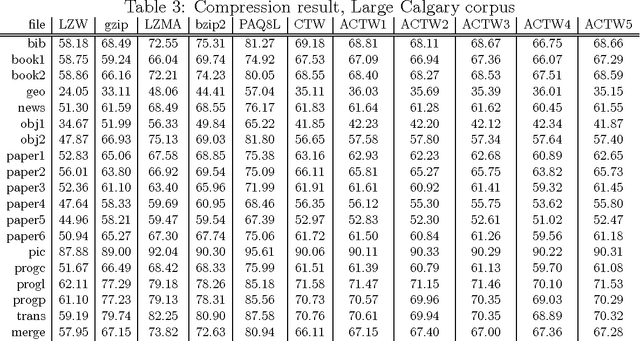
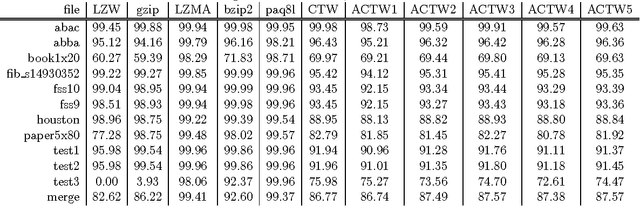
We describe an adaptive context tree weighting (ACTW) algorithm, as an extension to the standard context tree weighting (CTW) algorithm. Unlike the standard CTW algorithm, which weights all observations equally regardless of the depth, ACTW gives increasing weight to more recent observations, aiming to improve performance in cases where the input sequence is from a non-stationary distribution. Data compression results show ACTW variants improving over CTW on merged files from standard compression benchmark tests while never being significantly worse on any individual file.

Principles of Solomonoff Induction and AIXI

We identify principles characterizing Solomonoff Induction by demands on an agent's external behaviour. Key concepts are rationality, computability, indifference and time consistency. Furthermore, we discuss extensions to the full AI case to derive AIXI.

No Free Lunch versus Occam's Razor in Supervised Learning

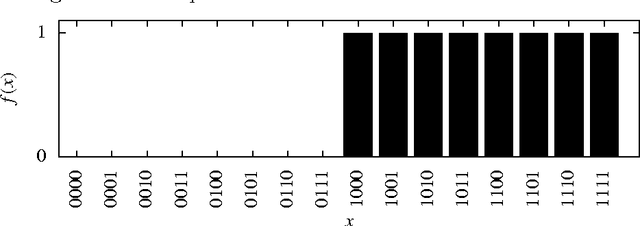
The No Free Lunch theorems are often used to argue that domain specific knowledge is required to design successful algorithms. We use algorithmic information theory to argue the case for a universal bias allowing an algorithm to succeed in all interesting problem domains. Additionally, we give a new algorithm for off-line classification, inspired by Solomonoff induction, with good performance on all structured problems under reasonable assumptions. This includes a proof of the efficacy of the well-known heuristic of randomly selecting training data in the hope of reducing misclassification rates.

Feature Reinforcement Learning In Practice

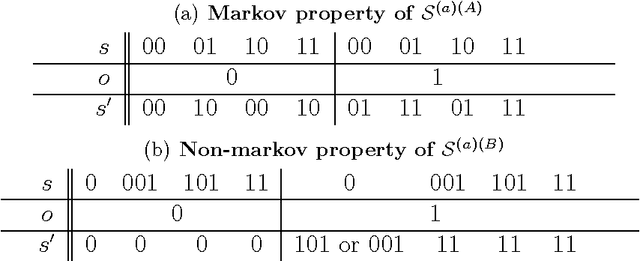
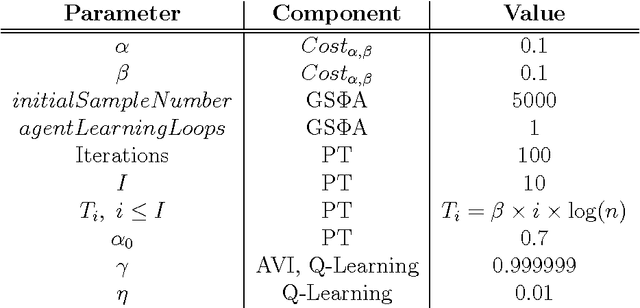
Following a recent surge in using history-based methods for resolving perceptual aliasing in reinforcement learning, we introduce an algorithm based on the feature reinforcement learning framework called PhiMDP. To create a practical algorithm we devise a stochastic search procedure for a class of context trees based on parallel tempering and a specialized proposal distribution. We provide the first empirical evaluation for PhiMDP. Our proposed algorithm achieves superior performance to the classical U-tree algorithm and the recent active-LZ algorithm, and is competitive with MC-AIXI-CTW that maintains a bayesian mixture over all context trees up to a chosen depth.We are encouraged by our ability to compete with this sophisticated method using an algorithm that simply picks one single model, and uses Q-learning on the corresponding MDP. Our PhiMDP algorithm is much simpler, yet consumes less time and memory. These results show promise for our future work on attacking more complex and larger problems.

Asymptotically Optimal Agents

Artificial general intelligence aims to create agents capable of learning to solve arbitrary interesting problems. We define two versions of asymptotic optimality and prove that no agent can satisfy the strong version while in some cases, depending on discounting, there does exist a non-computable weak asymptotically optimal agent.

Universal Prediction of Selected Bits

Many learning tasks can be viewed as sequence prediction problems. For example, online classification can be converted to sequence prediction with the sequence being pairs of input/target data and where the goal is to correctly predict the target data given input data and previous input/target pairs. Solomonoff induction is known to solve the general sequence prediction problem, but only if the entire sequence is sampled from a computable distribution. In the case of classification and discriminative learning though, only the targets need be structured (given the inputs). We show that the normalised version of Solomonoff induction can still be used in this case, and more generally that it can detect any recursive sub-pattern (regularity) within an otherwise completely unstructured sequence. It is also shown that the unnormalised version can fail to predict very simple recursive sub-patterns.