Small molecule retrieval from tandem mass spectrometry: what are we optimizing for?

One of the central challenges in the computational analysis of liquid chromatography-tandem mass spectrometry (LC-MS/MS) data is to identify the compounds underlying the output spectra. In recent years, this problem is increasingly tackled using deep learning methods. A common strategy involves predicting a molecular fingerprint vector from an input mass spectrum, which is then used to search for matches in a chemical compound database. While various loss functions are employed in training these predictive models, their impact on model performance remains poorly understood. In this study, we investigate commonly used loss functions, deriving novel regret bounds that characterize when Bayes-optimal decisions for these objectives must diverge. Our results reveal a fundamental trade-off between the two objectives of (1) fingerprint similarity and (2) molecular retrieval. Optimizing for more accurate fingerprint predictions typically worsens retrieval results, and vice versa. Our theoretical analysis shows this trade-off depends on the similarity structure of candidate sets, providing guidance for loss function and fingerprint selection.

Confidence Sequences for Generalized Linear Models via Regret Analysis

We develop a methodology for constructing confidence sets for parameters of statistical models via a reduction to sequential prediction. Our key observation is that for any generalized linear model (GLM), one can construct an associated game of sequential probability assignment such that achieving low regret in the game implies a high-probability upper bound on the excess likelihood of the true parameter of the GLM. This allows us to develop a scheme that we call online-to-confidence-set conversions, which effectively reduces the problem of proving the desired statistical claim to an algorithmic question. We study two varieties of this conversion scheme: 1) analytical conversions that only require proving the existence of algorithms with low regret and provide confidence sets centered at the maximum-likelihood estimator 2) algorithmic conversions that actively leverage the output of the online algorithm to construct confidence sets (and may be centered at other, adaptively constructed point estimators). The resulting methodology recovers all state-of-the-art confidence set constructions within a single framework, and also provides several new types of confidence sets that were previously unknown in the literature.

A General Online Algorithm for Optimizing Complex Performance Metrics

We consider sequential maximization of performance metrics that are general functions of a confusion matrix of a classifier (such as precision, F-measure, or G-mean). Such metrics are, in general, non-decomposable over individual instances, making their optimization very challenging. While they have been extensively studied under different frameworks in the batch setting, their analysis in the online learning regime is very limited, with only a few distinguished exceptions. In this paper, we introduce and analyze a general online algorithm that can be used in a straightforward way with a variety of complex performance metrics in binary, multi-class, and multi-label classification problems. The algorithm's update and prediction rules are appealingly simple and computationally efficient without the need to store any past data. We show the algorithm attains $\mathcal{O}(\frac{\ln n}{n})$ regret for concave and smooth metrics and verify the efficiency of the proposed algorithm in empirical studies.

Noise misleads rotation invariant algorithms on sparse targets

It is well known that the class of rotation invariant algorithms are suboptimal even for learning sparse linear problems when the number of examples is below the "dimension" of the problem. This class includes any gradient descent trained neural net with a fully-connected input layer (initialized with a rotationally symmetric distribution). The simplest sparse problem is learning a single feature out of $d$ features. In that case the classification error or regression loss grows with $1-k/n$ where $k$ is the number of examples seen. These lower bounds become vacuous when the number of examples $k$ reaches the dimension $d$. We show that when noise is added to this sparse linear problem, rotation invariant algorithms are still suboptimal after seeing $d$ or more examples. We prove this via a lower bound for the Bayes optimal algorithm on a rotationally symmetrized problem. We then prove much lower upper bounds on the same problem for simple non-rotation invariant algorithms. Finally we analyze the gradient flow trajectories of many standard optimization algorithms in some simple cases and show how they veer toward or away from the sparse targets. We believe that our trajectory categorization will be useful in designing algorithms that can exploit sparse targets and our method for proving lower bounds will be crucial for analyzing other families of algorithms that admit different classes of invariances.

Consistent algorithms for multi-label classification with macro-at-$k$ metrics

We consider the optimization of complex performance metrics in multi-label classification under the population utility framework. We mainly focus on metrics linearly decomposable into a sum of binary classification utilities applied separately to each label with an additional requirement of exactly $k$ labels predicted for each instance. These "macro-at-$k$" metrics possess desired properties for extreme classification problems with long tail labels. Unfortunately, the at-$k$ constraint couples the otherwise independent binary classification tasks, leading to a much more challenging optimization problem than standard macro-averages. We provide a statistical framework to study this problem, prove the existence and the form of the optimal classifier, and propose a statistically consistent and practical learning algorithm based on the Frank-Wolfe method. Interestingly, our main results concern even more general metrics being non-linear functions of label-wise confusion matrices. Empirical results provide evidence for the competitive performance of the proposed approach.

Generalized test utilities for long-tail performance in extreme multi-label classification

Extreme multi-label classification (XMLC) is the task of selecting a small subset of relevant labels from a very large set of possible labels. As such, it is characterized by long-tail labels, i.e., most labels have very few positive instances. With standard performance measures such as precision@k, a classifier can ignore tail labels and still report good performance. However, it is often argued that correct predictions in the tail are more interesting or rewarding, but the community has not yet settled on a metric capturing this intuitive concept. The existing propensity-scored metrics fall short on this goal by confounding the problems of long-tail and missing labels. In this paper, we analyze generalized metrics budgeted "at k" as an alternative solution. To tackle the challenging problem of optimizing these metrics, we formulate it in the expected test utility (ETU) framework, which aims at optimizing the expected performance on a fixed test set. We derive optimal prediction rules and construct computationally efficient approximations with provable regret guarantees and robustness against model misspecification. Our algorithm, based on block coordinate ascent, scales effortlessly to XMLC problems and obtains promising results in terms of long-tail performance.

Learning from Randomly Initialized Neural Network Features

We present the surprising result that randomly initialized neural networks are good feature extractors in expectation. These random features correspond to finite-sample realizations of what we call Neural Network Prior Kernel (NNPK), which is inherently infinite-dimensional. We conduct ablations across multiple architectures of varying sizes as well as initializations and activation functions. Our analysis suggests that certain structures that manifest in a trained model are already present at initialization. Therefore, NNPK may provide further insight into why neural networks are so effective in learning such structures.

Robust Online Convex Optimization in the Presence of Outliers

We consider online convex optimization when a number k of data points are outliers that may be corrupted. We model this by introducing the notion of robust regret, which measures the regret only on rounds that are not outliers. The aim for the learner is to achieve small robust regret, without knowing where the outliers are. If the outliers are chosen adversarially, we show that a simple filtering strategy on extreme gradients incurs O(k) additive overhead compared to the usual regret bounds, and that this is unimprovable, which means that k needs to be sublinear in the number of rounds. We further ask which additional assumptions would allow for a linear number of outliers. It turns out that the usual benign cases of independently, identically distributed (i.i.d.) observations or strongly convex losses are not sufficient. However, combining i.i.d. observations with the assumption that outliers are those observations that are in an extreme quantile of the distribution, does lead to sublinear robust regret, even though the expected number of outliers is linear.

A case where a spindly two-layer linear network whips any neural network with a fully connected input layer

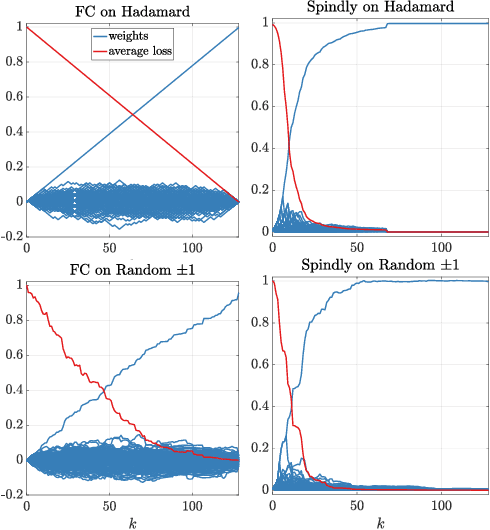
It was conjectured that any neural network of any structure and arbitrary differentiable transfer functions at the nodes cannot learn the following problem sample efficiently when trained with gradient descent: The instances are the rows of a $d$-dimensional Hadamard matrix and the target is one of the features, i.e. very sparse. We essentially prove this conjecture: We show that after receiving a random training set of size $k < d$, the expected square loss is still $1-\frac{k}{(d-1)}$. The only requirement needed is that the input layer is fully connected and the initial weight vectors of the input nodes are chosen from a rotation invariant distribution. Surprisingly the same type of problem can be solved drastically more efficient by a simple 2-layer linear neural network in which the $d$ inputs are connected to the output node by chains of length 2 (Now the input layer has only one edge per input). When such a network is trained by gradient descent, then it has been shown that its expected square loss is $\frac{\log d}{k}$. Our lower bounds essentially show that a sparse input layer is needed to sample efficiently learn sparse targets with gradient descent when the number of examples is less than the number of input features.

Adaptive scale-invariant online algorithms for learning linear models

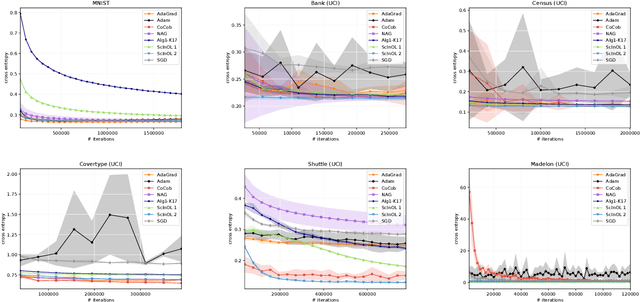
We consider online learning with linear models, where the algorithm predicts on sequentially revealed instances (feature vectors), and is compared against the best linear function (comparator) in hindsight. Popular algorithms in this framework, such as Online Gradient Descent (OGD), have parameters (learning rates), which ideally should be tuned based on the scales of the features and the optimal comparator, but these quantities only become available at the end of the learning process. In this paper, we resolve the tuning problem by proposing online algorithms making predictions which are invariant under arbitrary rescaling of the features. The algorithms have no parameters to tune, do not require any prior knowledge on the scale of the instances or the comparator, and achieve regret bounds matching (up to a logarithmic factor) that of OGD with optimally tuned separate learning rates per dimension, while retaining comparable runtime performance.