Design Considerations in Offline Preference-based RL

Offline algorithms for Reinforcement Learning from Human Preferences (RLHF), which use only a fixed dataset of sampled responses given an input, and preference feedback among these responses, have gained increasing prominence in the literature on aligning language models. In this paper, we study how the different design choices made in methods such as DPO, IPO, SLiC and many variants influence the quality of the learned policy, from a theoretical perspective. Our treatment yields insights into the choices of loss function, the policy which is used to normalize log-likelihoods, and also the role of the data sampling policy. Notably, our results do not rely on the standard reparameterization-style arguments used to motivate some of the algorithms in this family, which allows us to give a unified treatment to a broad class of methods. We also conduct a small empirical study to verify some of the theoretical findings on a standard summarization benchmark.

Incentive-compatible Bandits: Importance Weighting No More

We study the problem of incentive-compatible online learning with bandit feedback. In this class of problems, the experts are self-interested agents who might misrepresent their preferences with the goal of being selected most often. The goal is to devise algorithms which are simultaneously incentive-compatible, that is the experts are incentivised to report their true preferences, and have no regret with respect to the preferences of the best fixed expert in hindsight. \citet{freeman2020no} propose an algorithm in the full information setting with optimal $O(\sqrt{T \log(K)})$ regret and $O(T^{2/3}(K\log(K))^{1/3})$ regret in the bandit setting. In this work we propose the first incentive-compatible algorithms that enjoy $O(\sqrt{KT})$ regret bounds. We further demonstrate how simple loss-biasing allows the algorithm proposed in Freeman et al. 2020 to enjoy $\tilde O(\sqrt{KT})$ regret. As a byproduct of our approach we obtain the first bandit algorithm with nearly optimal regret bounds in the adversarial setting which works entirely on the observed loss sequence without the need for importance-weighted estimators. Finally, we provide an incentive-compatible algorithm that enjoys asymptotically optimal best-of-both-worlds regret guarantees, i.e., logarithmic regret in the stochastic regime as well as worst-case $O(\sqrt{KT})$ regret.

Offline Imitation Learning from Multiple Baselines with Applications to Compiler Optimization

This work studies a Reinforcement Learning (RL) problem in which we are given a set of trajectories collected with K baseline policies. Each of these policies can be quite suboptimal in isolation, and have strong performance in complementary parts of the state space. The goal is to learn a policy which performs as well as the best combination of baselines on the entire state space. We propose a simple imitation learning based algorithm, show a sample complexity bound on its accuracy and prove that the the algorithm is minimax optimal by showing a matching lower bound. Further, we apply the algorithm in the setting of machine learning guided compiler optimization to learn policies for inlining programs with the objective of creating a small binary. We demonstrate that we can learn a policy that outperforms an initial policy learned via standard RL through a few iterations of our approach.

A Mechanism for Sample-Efficient In-Context Learning for Sparse Retrieval Tasks

We study the phenomenon of \textit{in-context learning} (ICL) exhibited by large language models, where they can adapt to a new learning task, given a handful of labeled examples, without any explicit parameter optimization. Our goal is to explain how a pre-trained transformer model is able to perform ICL under reasonable assumptions on the pre-training process and the downstream tasks. We posit a mechanism whereby a transformer can achieve the following: (a) receive an i.i.d. sequence of examples which have been converted into a prompt using potentially-ambiguous delimiters, (b) correctly segment the prompt into examples and labels, (c) infer from the data a \textit{sparse linear regressor} hypothesis, and finally (d) apply this hypothesis on the given test example and return a predicted label. We establish that this entire procedure is implementable using the transformer mechanism, and we give sample complexity guarantees for this learning framework. Our empirical findings validate the challenge of segmentation, and we show a correspondence between our posited mechanisms and observed attention maps for step (c).

Leveraging User-Triggered Supervision in Contextual Bandits

We study contextual bandit (CB) problems, where the user can sometimes respond with the best action in a given context. Such an interaction arises, for example, in text prediction or autocompletion settings, where a poor suggestion is simply ignored and the user enters the desired text instead. Crucially, this extra feedback is user-triggered on only a subset of the contexts. We develop a new framework to leverage such signals, while being robust to their biased nature. We also augment standard CB algorithms to leverage the signal, and show improved regret guarantees for the resulting algorithms under a variety of conditions on the helpfulness of and bias inherent in this feedback.

Stochastic Online Learning with Feedback Graphs: Finite-Time and Asymptotic Optimality

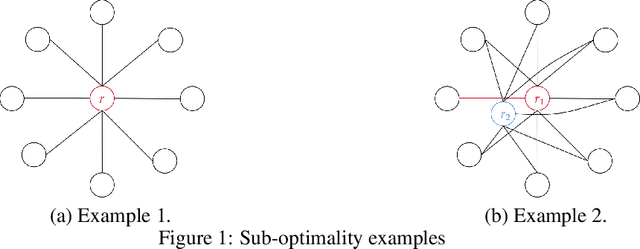
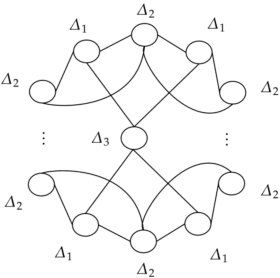
We revisit the problem of stochastic online learning with feedback graphs, with the goal of devising algorithms that are optimal, up to constants, both asymptotically and in finite time. We show that, surprisingly, the notion of optimal finite-time regret is not a uniquely defined property in this context and that, in general, it is decoupled from the asymptotic rate. We discuss alternative choices and propose a notion of finite-time optimality that we argue is \emph{meaningful}. For that notion, we give an algorithm that admits quasi-optimal regret both in finite-time and asymptotically.

The Pareto Frontier of model selection for general Contextual Bandits

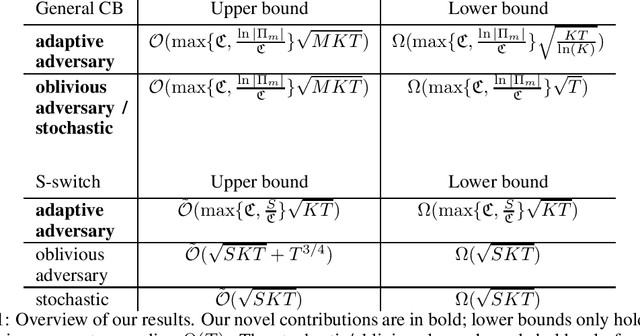
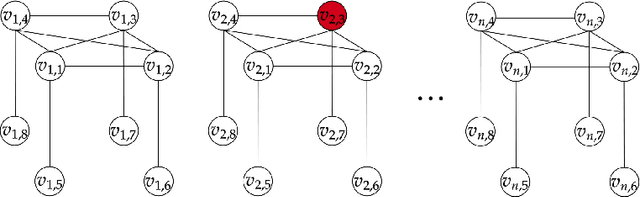
Recent progress in model selection raises the question of the fundamental limits of these techniques. Under specific scrutiny has been model selection for general contextual bandits with nested policy classes, resulting in a COLT2020 open problem. It asks whether it is possible to obtain simultaneously the optimal single algorithm guarantees over all policies in a nested sequence of policy classes, or if otherwise this is possible for a trade-off $\alpha\in[\frac{1}{2},1)$ between complexity term and time: $\ln(|\Pi_m|)^{1-\alpha}T^\alpha$. We give a disappointing answer to this question. Even in the purely stochastic regime, the desired results are unobtainable. We present a Pareto frontier of up to logarithmic factors matching upper and lower bounds, thereby proving that an increase in the complexity term $\ln(|\Pi_m|)$ independent of $T$ is unavoidable for general policy classes. As a side result, we also resolve a COLT2016 open problem concerning second-order bounds in full-information games.

Beyond Value-Function Gaps: Improved Instance-Dependent Regret Bounds for Episodic Reinforcement Learning

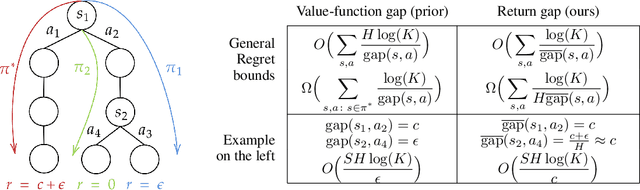
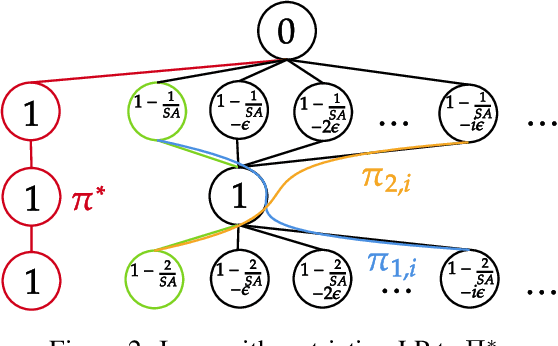
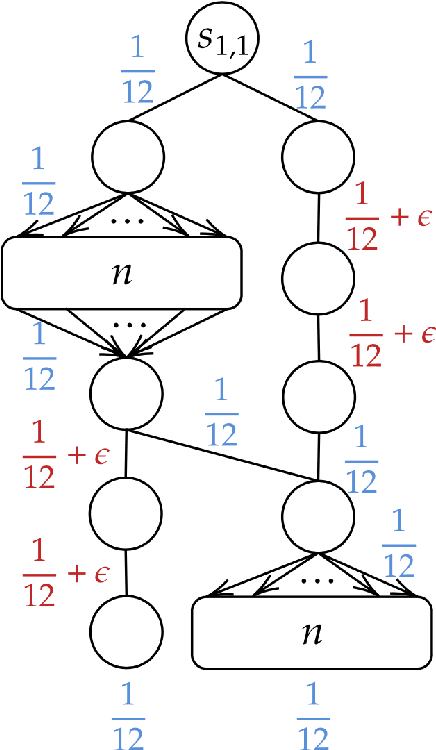
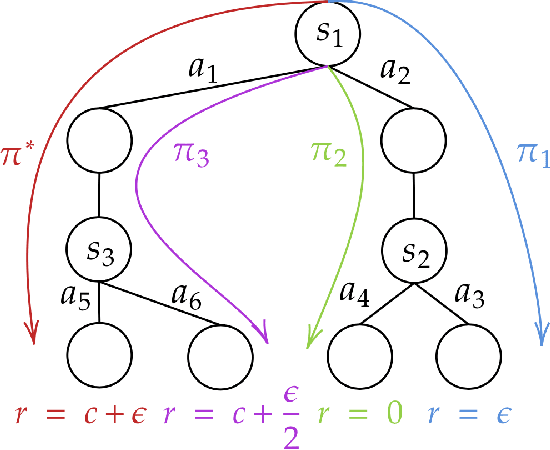
We provide improved gap-dependent regret bounds for reinforcement learning in finite episodic Markov decision processes. Compared to prior work, our bounds depend on alternative definitions of gaps. These definitions are based on the insight that, in order to achieve a favorable regret, an algorithm does not need to learn how to behave optimally in states that are not reached by an optimal policy. We prove tighter upper regret bounds for optimistic algorithms and accompany them with new information-theoretic lower bounds for a large class of MDPs. Our results show that optimistic algorithms can not achieve the information-theoretic lower bounds even in deterministic MDPs unless there is a unique optimal policy.

Corralling Stochastic Bandit Algorithms

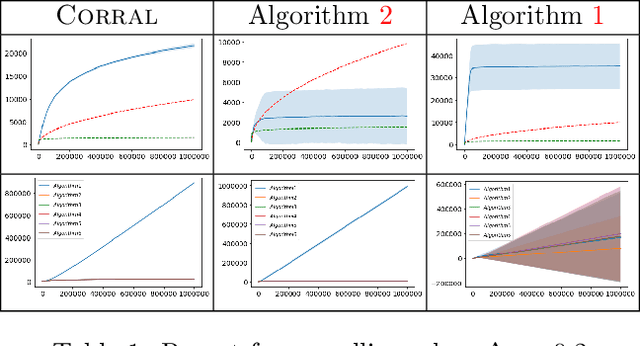
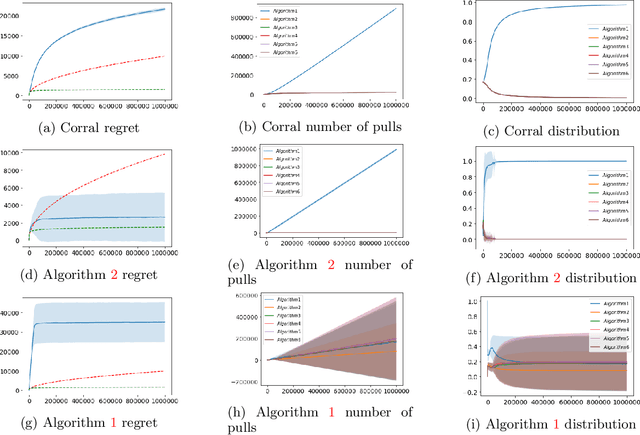
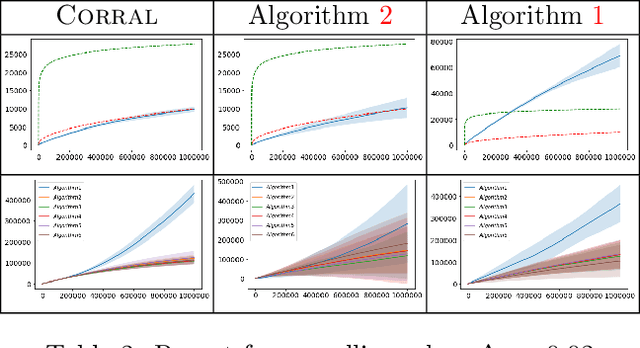
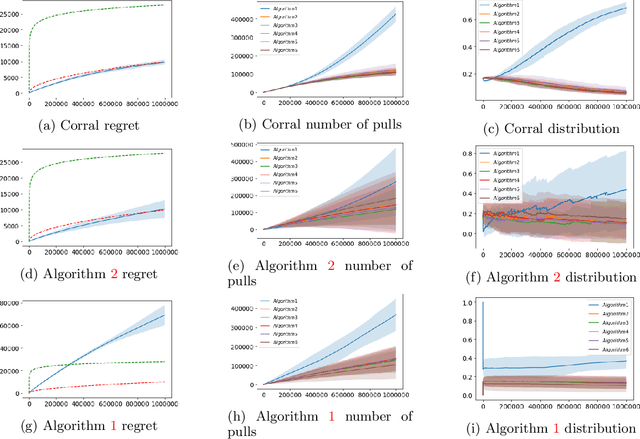
We study the problem of corralling stochastic bandit algorithms, that is combining multiple bandit algorithms designed for a stochastic environment, with the goal of devising a corralling algorithm that performs almost as well as the best base algorithm. We give two general algorithms for this setting, which we show benefit from favorable regret guarantees. We show that the regret of the corralling algorithms is no worse than that of the best algorithm containing the arm with the highest reward, and depends on the gap between the highest reward and other rewards. We also provide lower bounds for this problem that further justify our approach.

Private Stochastic Convex Optimization: Efficient Algorithms for Non-smooth Objectives

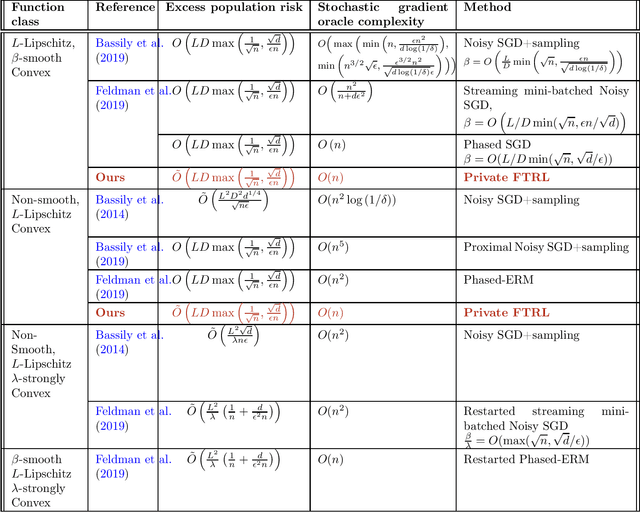
In this paper, we revisit the problem of private stochastic convex optimization. We propose an algorithm, based on noisy mirror descent, which achieves optimal rates up to a logarithmic factor, both in terms of statistical complexity and number of queries to a first-order stochastic oracle. Unlike prior work, we do not require Lipschitz continuity of stochastic gradients to achieve optimal rates. Our algorithm generalizes beyond the Euclidean setting and yields anytime utility and privacy guarantees.