Towards Exact Gradient-based Training on Analog In-memory Computing

Given the high economic and environmental costs of using large vision or language models, analog in-memory accelerators present a promising solution for energy-efficient AI. While inference on analog accelerators has been studied recently, the training perspective is underexplored. Recent studies have shown that the "workhorse" of digital AI training - stochastic gradient descent (SGD) algorithm converges inexactly when applied to model training on non-ideal devices. This paper puts forth a theoretical foundation for gradient-based training on analog devices. We begin by characterizing the non-convergent issue of SGD, which is caused by the asymmetric updates on the analog devices. We then provide a lower bound of the asymptotic error to show that there is a fundamental performance limit of SGD-based analog training rather than an artifact of our analysis. To address this issue, we study a heuristic analog algorithm called Tiki-Taka that has recently exhibited superior empirical performance compared to SGD and rigorously show its ability to exactly converge to a critical point and hence eliminates the asymptotic error. The simulations verify the correctness of the analyses.

Using the IBM Analog In-Memory Hardware Acceleration Kit for Neural Network Training and Inference

Analog In-Memory Computing (AIMC) is a promising approach to reduce the latency and energy consumption of Deep Neural Network (DNN) inference and training. However, the noisy and non-linear device characteristics, and the non-ideal peripheral circuitry in AIMC chips, require adapting DNNs to be deployed on such hardware to achieve equivalent accuracy to digital computing. In this tutorial, we provide a deep dive into how such adaptations can be achieved and evaluated using the recently released IBM Analog Hardware Acceleration Kit (AIHWKit), freely available at https://github.com/IBM/aihwkit. The AIHWKit is a Python library that simulates inference and training of DNNs using AIMC. We present an in-depth description of the AIHWKit design, functionality, and best practices to properly perform inference and training. We also present an overview of the Analog AI Cloud Composer, that provides the benefits of using the AIHWKit simulation platform in a fully managed cloud setting. Finally, we show examples on how users can expand and customize AIHWKit for their own needs. This tutorial is accompanied by comprehensive Jupyter Notebook code examples that can be run using AIHWKit, which can be downloaded from https://github.com/IBM/aihwkit/tree/master/notebooks/tutorial.

Fast offset corrected in-memory training

In-memory computing with resistive crossbar arrays has been suggested to accelerate deep-learning workloads in highly efficient manner. To unleash the full potential of in-memory computing, it is desirable to accelerate the training as well as inference for large deep neural networks (DNNs). In the past, specialized in-memory training algorithms have been proposed that not only accelerate the forward and backward passes, but also establish tricks to update the weight in-memory and in parallel. However, the state-of-the-art algorithm (Tiki-Taka version 2 (TTv2)) still requires near perfect offset correction and suffers from potential biases that might occur due to programming and estimation inaccuracies, as well as longer-term instabilities of the device materials. Here we propose and describe two new and improved algorithms for in-memory computing (Chopped-TTv2 (c-TTv2) and Analog Gradient Accumulation with Dynamic reference (AGAD)), that retain the same runtime complexity but correct for any remaining offsets using choppers. These algorithms greatly relax the device requirements and thus expanding the scope of possible materials potentially employed for such fast in-memory DNN training.

Hardware-aware training for large-scale and diverse deep learning inference workloads using in-memory computing-based accelerators

Analog in-memory computing (AIMC) -- a promising approach for energy-efficient acceleration of deep learning workloads -- computes matrix-vector multiplications (MVMs) but only approximately, due to nonidealities that often are non-deterministic or nonlinear. This can adversely impact the achievable deep neural network (DNN) inference accuracy as compared to a conventional floating point (FP) implementation. While retraining has previously been suggested to improve robustness, prior work has explored only a few DNN topologies, using disparate and overly simplified AIMC hardware models. Here, we use hardware-aware (HWA) training to systematically examine the accuracy of AIMC for multiple common artificial intelligence (AI) workloads across multiple DNN topologies, and investigate sensitivity and robustness to a broad set of nonidealities. By introducing a new and highly realistic AIMC crossbar-model, we improve significantly on earlier retraining approaches. We show that many large-scale DNNs of various topologies, including convolutional neural networks (CNNs), recurrent neural networks (RNNs), and transformers, can in fact be successfully retrained to show iso-accuracy on AIMC. Our results further suggest that AIMC nonidealities that add noise to the inputs or outputs, not the weights, have the largest impact on DNN accuracy, and that RNNs are particularly robust to all nonidealities.

A flexible and fast PyTorch toolkit for simulating training and inference on analog crossbar arrays

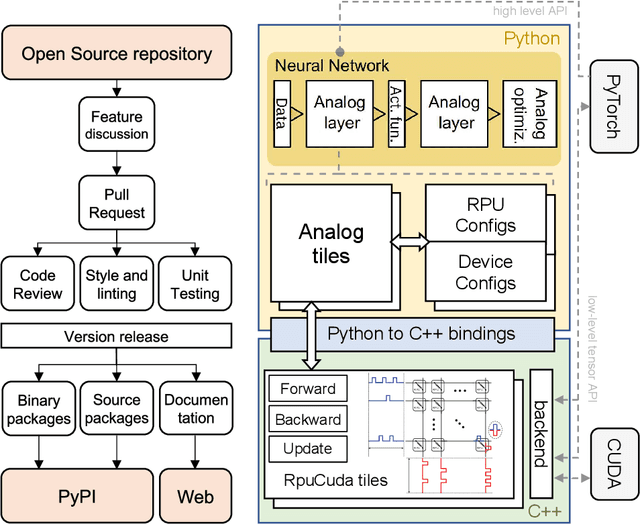
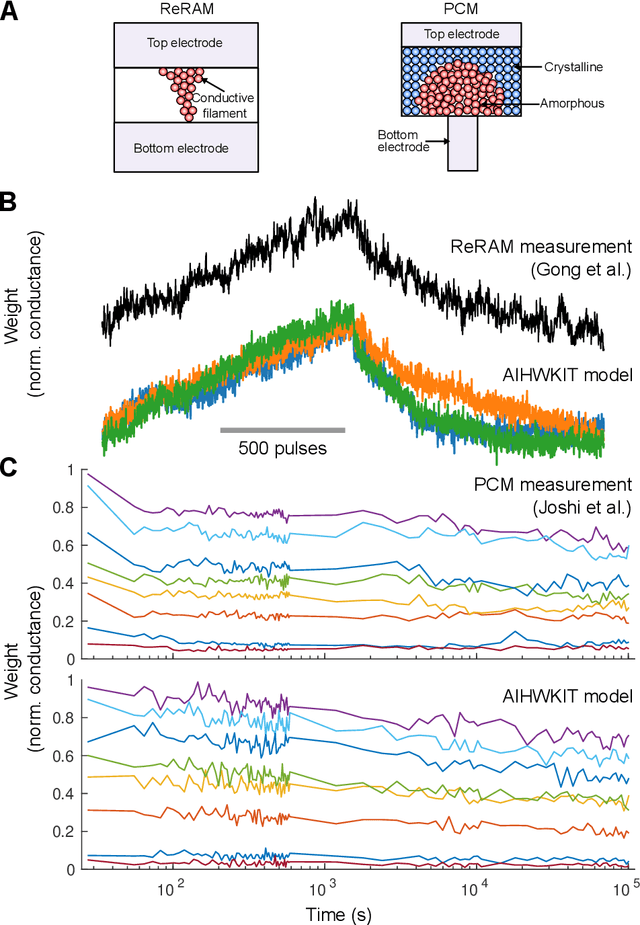
We introduce the IBM Analog Hardware Acceleration Kit, a new and first of a kind open source toolkit to simulate analog crossbar arrays in a convenient fashion from within PyTorch (freely available at https://github.com/IBM/aihwkit). The toolkit is under active development and is centered around the concept of an "analog tile" which captures the computations performed on a crossbar array. Analog tiles are building blocks that can be used to extend existing network modules with analog components and compose arbitrary artificial neural networks (ANNs) using the flexibility of the PyTorch framework. Analog tiles can be conveniently configured to emulate a plethora of different analog hardware characteristics and their non-idealities, such as device-to-device and cycle-to-cycle variations, resistive device response curves, and weight and output noise. Additionally, the toolkit makes it possible to design custom unit cell configurations and to use advanced analog optimization algorithms such as Tiki-Taka. Moreover, the backward and update behavior can be set to "ideal" to enable hardware-aware training features for chips that target inference acceleration only. To evaluate the inference accuracy of such chips over time, we provide statistical programming noise and drift models calibrated on phase-change memory hardware. Our new toolkit is fully GPU accelerated and can be used to conveniently estimate the impact of material properties and non-idealities of future analog technology on the accuracy for arbitrary ANNs.

Training large-scale ANNs on simulated resistive crossbar arrays

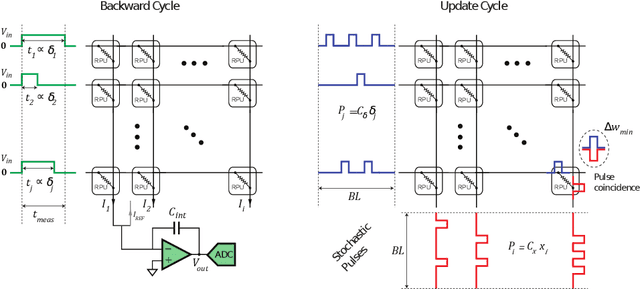
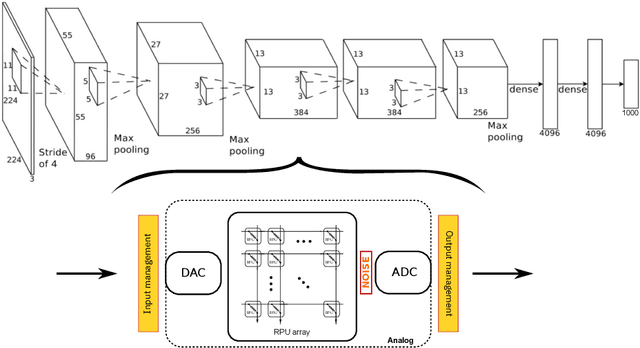
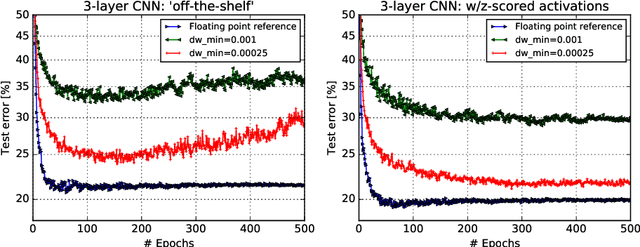
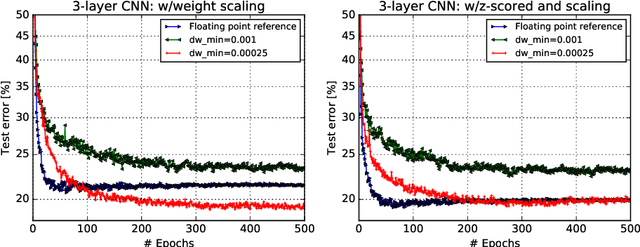
Accelerating training of artificial neural networks (ANN) with analog resistive crossbar arrays is a promising idea. While the concept has been verified on very small ANNs and toy data sets (such as MNIST), more realistically sized ANNs and datasets have not yet been tackled. However, it is to be expected that device materials and hardware design constraints, such as noisy computations, finite number of resistive states of the device materials, saturating weight and activation ranges, and limited precision of analog-to-digital converters, will cause significant challenges to the successful training of state-of-the-art ANNs. By using analog hardware aware ANN training simulations, we here explore a number of simple algorithmic compensatory measures to cope with analog noise and limited weight and output ranges and resolutions, that dramatically improve the simulated training performances on RPU arrays on intermediately to large-scale ANNs.

Efficient ConvNets for Analog Arrays

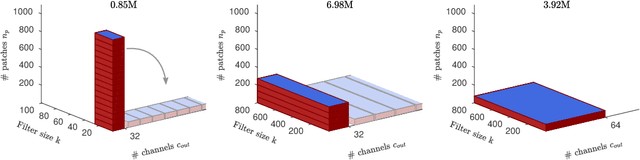
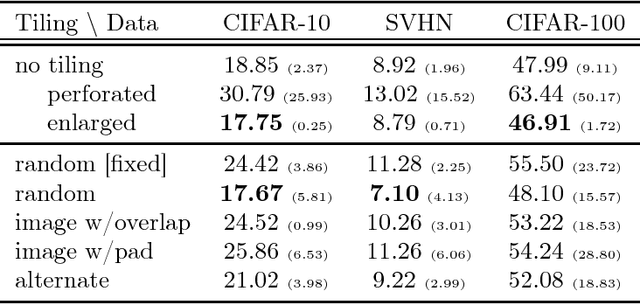
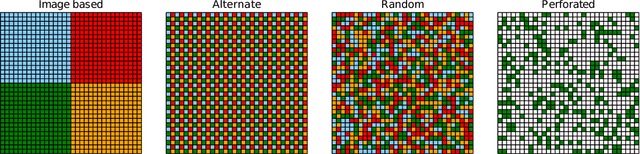
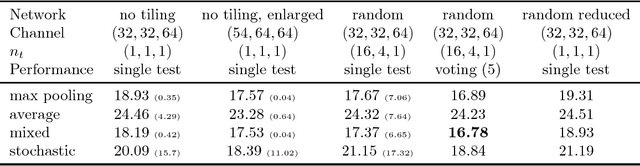
Analog arrays are a promising upcoming hardware technology with the potential to drastically speed up deep learning. Their main advantage is that they compute matrix-vector products in constant time, irrespective of the size of the matrix. However, early convolution layers in ConvNets map very unfavorably onto analog arrays, because kernel matrices are typically small and the constant time operation needs to be sequentially iterated a large number of times, reducing the speed up advantage for ConvNets. Here, we propose to replicate the kernel matrix of a convolution layer on distinct analog arrays, and randomly divide parts of the compute among them, so that multiple kernel matrices are trained in parallel. With this modification, analog arrays execute ConvNets with an acceleration factor that is proportional to the number of kernel matrices used per layer (here tested 16-128). Despite having more free parameters, we show analytically and in numerical experiments that this convolution architecture is self-regularizing and implicitly learns similar filters across arrays. We also report superior performance on a number of datasets and increased robustness to adversarial attacks. Our investigation suggests to revise the notion that mixed analog-digital hardware is not suitable for ConvNets.

A Kernel Method for the Two-Sample Problem

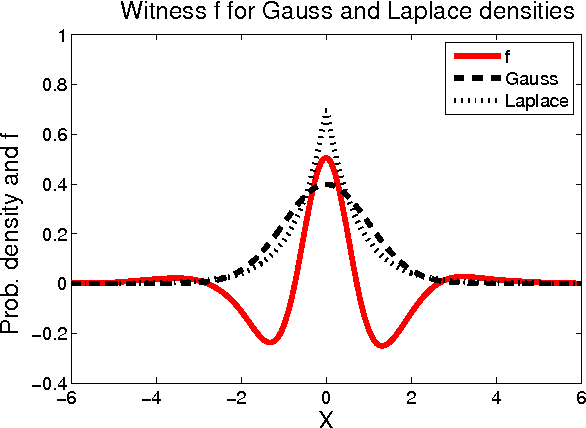
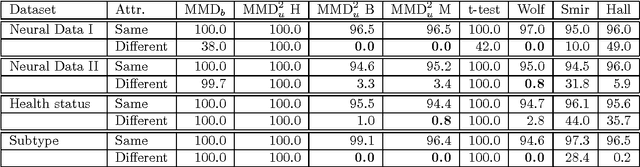
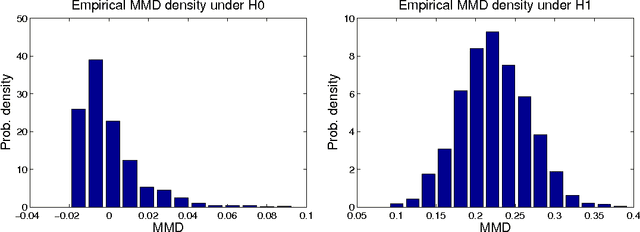
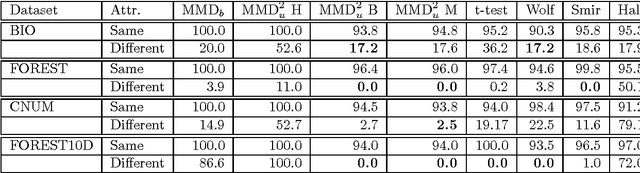
We propose a framework for analyzing and comparing distributions, allowing us to design statistical tests to determine if two samples are drawn from different distributions. Our test statistic is the largest difference in expectations over functions in the unit ball of a reproducing kernel Hilbert space (RKHS). We present two tests based on large deviation bounds for the test statistic, while a third is based on the asymptotic distribution of this statistic. The test statistic can be computed in quadratic time, although efficient linear time approximations are available. Several classical metrics on distributions are recovered when the function space used to compute the difference in expectations is allowed to be more general (eg. a Banach space). We apply our two-sample tests to a variety of problems, including attribute matching for databases using the Hungarian marriage method, where they perform strongly. Excellent performance is also obtained when comparing distributions over graphs, for which these are the first such tests.