Efficient ConvNets for Analog Arrays
Paper and Code
Jul 03, 2018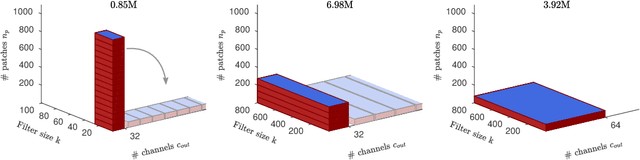
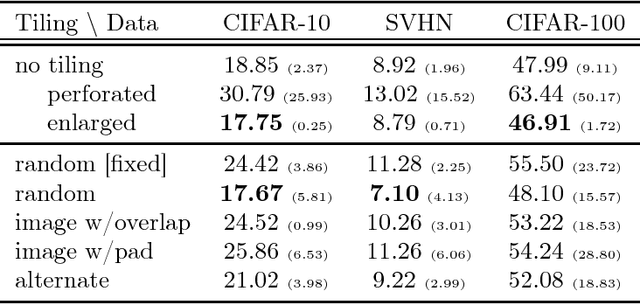
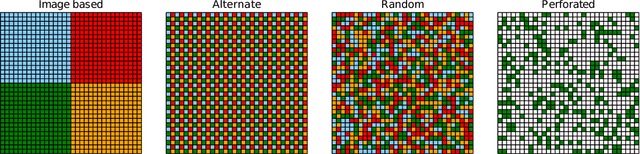
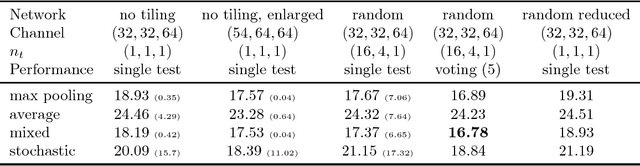
Analog arrays are a promising upcoming hardware technology with the potential to drastically speed up deep learning. Their main advantage is that they compute matrix-vector products in constant time, irrespective of the size of the matrix. However, early convolution layers in ConvNets map very unfavorably onto analog arrays, because kernel matrices are typically small and the constant time operation needs to be sequentially iterated a large number of times, reducing the speed up advantage for ConvNets. Here, we propose to replicate the kernel matrix of a convolution layer on distinct analog arrays, and randomly divide parts of the compute among them, so that multiple kernel matrices are trained in parallel. With this modification, analog arrays execute ConvNets with an acceleration factor that is proportional to the number of kernel matrices used per layer (here tested 16-128). Despite having more free parameters, we show analytically and in numerical experiments that this convolution architecture is self-regularizing and implicitly learns similar filters across arrays. We also report superior performance on a number of datasets and increased robustness to adversarial attacks. Our investigation suggests to revise the notion that mixed analog-digital hardware is not suitable for ConvNets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge