Risk-Averse Certification of Bayesian Neural Networks

In light of the inherently complex and dynamic nature of real-world environments, incorporating risk measures is crucial for the robustness evaluation of deep learning models. In this work, we propose a Risk-Averse Certification framework for Bayesian neural networks called RAC-BNN. Our method leverages sampling and optimisation to compute a sound approximation of the output set of a BNN, represented using a set of template polytopes. To enhance robustness evaluation, we integrate a coherent distortion risk measure--Conditional Value at Risk (CVaR)--into the certification framework, providing probabilistic guarantees based on empirical distributions obtained through sampling. We validate RAC-BNN on a range of regression and classification benchmarks and compare its performance with a state-of-the-art method. The results show that RAC-BNN effectively quantifies robustness under worst-performing risky scenarios, and achieves tighter certified bounds and higher efficiency in complex tasks.

Distributed Markov Chain Monte Carlo Sampling based on the Alternating Direction Method of Multipliers

Many machine learning applications require operating on a spatially distributed dataset. Despite technological advances, privacy considerations and communication constraints may prevent gathering the entire dataset in a central unit. In this paper, we propose a distributed sampling scheme based on the alternating direction method of multipliers, which is commonly used in the optimization literature due to its fast convergence. In contrast to distributed optimization, distributed sampling allows for uncertainty quantification in Bayesian inference tasks. We provide both theoretical guarantees of our algorithm's convergence and experimental evidence of its superiority to the state-of-the-art. For our theoretical results, we use convex optimization tools to establish a fundamental inequality on the generated local sample iterates. This inequality enables us to show convergence of the distribution associated with these iterates to the underlying target distribution in Wasserstein distance. In simulation, we deploy our algorithm on linear and logistic regression tasks and illustrate its fast convergence compared to existing gradient-based methods.

Correct-by-Construction Control for Stochastic and Uncertain Dynamical Models via Formal Abstractions

Automated synthesis of correct-by-construction controllers for autonomous systems is crucial for their deployment in safety-critical scenarios. Such autonomous systems are naturally modeled as stochastic dynamical models. The general problem is to compute a controller that provably satisfies a given task, represented as a probabilistic temporal logic specification. However, factors such as stochastic uncertainty, imprecisely known parameters, and hybrid features make this problem challenging. We have developed an abstraction framework that can be used to solve this problem under various modeling assumptions. Our approach is based on a robust finite-state abstraction of the stochastic dynamical model in the form of a Markov decision process with intervals of probabilities (iMDP). We use state-of-the-art verification techniques to compute an optimal policy on the iMDP with guarantees for satisfying the given specification. We then show that, by construction, we can refine this policy into a feedback controller for which these guarantees carry over to the dynamical model. In this short paper, we survey our recent research in this area and highlight two challenges (related to scalability and dealing with nonlinear dynamics) that we aim to address with our ongoing research.

Data-driven abstractions via adaptive refinements and a Kantorovich metric [extended version]

We introduce an adaptive refinement procedure for smart, and scalable abstraction of dynamical systems. Our technique relies on partitioning the state space depending on the observation of future outputs. However, this knowledge is dynamically constructed in an adaptive, asymmetric way. In order to learn the optimal structure, we define a Kantorovich-inspired metric between Markov chains, and we use it as a loss function. Our technique is prone to data-driven frameworks, but not restricted to. We also study properties of the above mentioned metric between Markov chains, which we believe could be of application for wider purpose. We propose an algorithm to approximate it, and we show that our method yields a much better computational complexity than using classical linear programming techniques.

Robust Control for Dynamical Systems With Non-Gaussian Noise via Formal Abstractions

Controllers for dynamical systems that operate in safety-critical settings must account for stochastic disturbances. Such disturbances are often modeled as process noise in a dynamical system, and common assumptions are that the underlying distributions are known and/or Gaussian. In practice, however, these assumptions may be unrealistic and can lead to poor approximations of the true noise distribution. We present a novel controller synthesis method that does not rely on any explicit representation of the noise distributions. In particular, we address the problem of computing a controller that provides probabilistic guarantees on safely reaching a target, while also avoiding unsafe regions of the state space. First, we abstract the continuous control system into a finite-state model that captures noise by probabilistic transitions between discrete states. As a key contribution, we adapt tools from the scenario approach to compute probably approximately correct (PAC) bounds on these transition probabilities, based on a finite number of samples of the noise. We capture these bounds in the transition probability intervals of a so-called interval Markov decision process (iMDP). This iMDP is, with a user-specified confidence probability, robust against uncertainty in the transition probabilities, and the tightness of the probability intervals can be controlled through the number of samples. We use state-of-the-art verification techniques to provide guarantees on the iMDP and compute a controller for which these guarantees carry over to the original control system. In addition, we develop a tailored computational scheme that reduces the complexity of the synthesis of these guarantees on the iMDP. Benchmarks on realistic control systems show the practical applicability of our method, even when the iMDP has hundreds of millions of transitions.

Formal Controller Synthesis for Markov Jump Linear Systems with Uncertain Dynamics

Automated synthesis of provably correct controllers for cyber-physical systems is crucial for deploying these systems in safety-critical scenarios. However, their hybrid features and stochastic or unknown behaviours make this synthesis problem challenging. In this paper, we propose a method for synthesizing controllers for Markov jump linear systems (MJLSs), a particular class of cyber-physical systems, that certifiably satisfy a requirement expressed as a specification in probabilistic computation tree logic (PCTL). An MJLS consists of a finite set of linear dynamics with unknown additive disturbances, where jumps between these modes are governed by a Markov decision process (MDP). We consider both the case where the transition function of this MDP is given by probability intervals or where it is completely unknown. Our approach is based on generating a finite-state abstraction which captures both the discrete and the continuous behaviour of the original system. We formalise such abstraction as an interval Markov decision process (iMDP): intervals of transition probabilities are computed using sampling techniques from the so-called "scenario approach", resulting in a probabilistically sound approximation of the MJLS. This iMDP abstracts both the jump dynamics between modes, as well as the continuous dynamics within the modes. To demonstrate the efficacy of our technique, we apply our method to multiple realistic benchmark problems, in particular, temperature control, and aerial vehicle delivery problems.

Probabilities Are Not Enough: Formal Controller Synthesis for Stochastic Dynamical Models with Epistemic Uncertainty

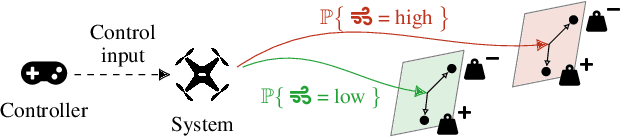
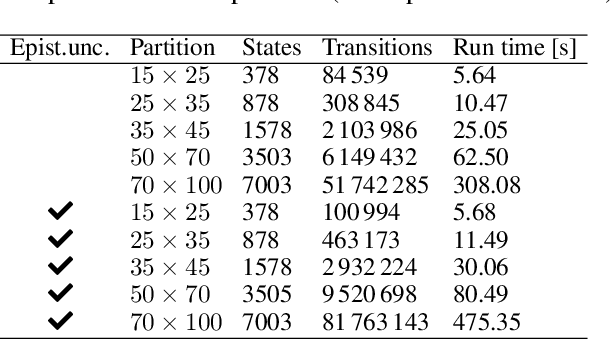
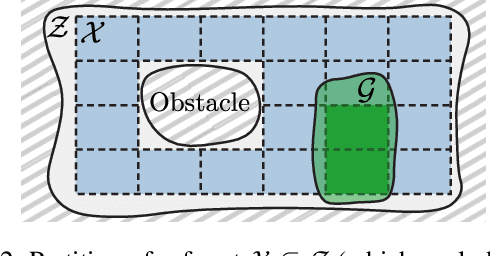
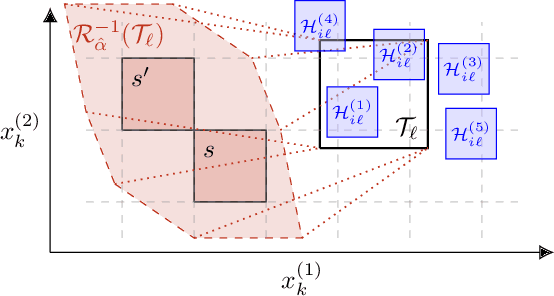
Capturing uncertainty in models of complex dynamical systems is crucial to designing safe controllers. Stochastic noise causes aleatoric uncertainty, whereas imprecise knowledge of model parameters and the presence of external disturbances lead to epistemic uncertainty. Several approaches use formal abstractions to synthesize policies that satisfy temporal specifications related to safety and reachability. However, the underlying models exclusively capture aleatoric but not epistemic uncertainty, and thus require that model parameters and disturbances are known precisely. Our contribution to overcoming this restriction is a novel abstraction-based controller synthesis method for continuous-state models with stochastic noise, uncertain parameters, and external disturbances. By sampling techniques and robust analysis, we capture both aleatoric and epistemic uncertainty, with a user-specified confidence level, in the transition probability intervals of a so-called interval Markov decision process (iMDP). We then synthesize an optimal policy on this abstract iMDP, which translates (with the specified confidence level) to a feedback controller for the continuous model, with the same performance guarantees. Our experimental benchmarks confirm that accounting for epistemic uncertainty leads to controllers that are more robust against variations in parameter values.

Observational Robustness and Invariances in Reinforcement Learning via Lexicographic Objectives

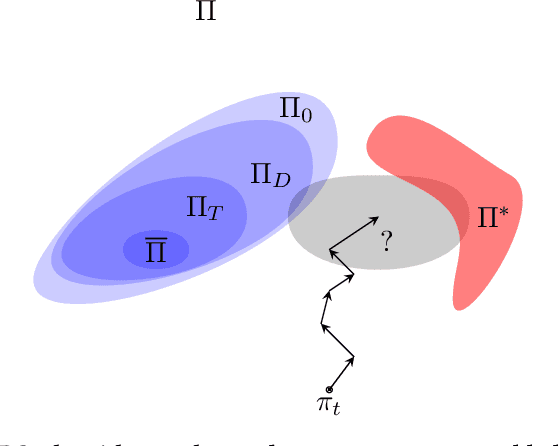
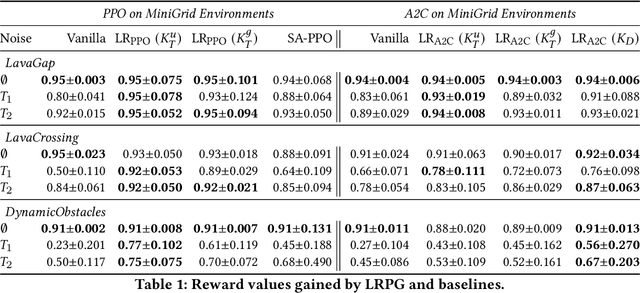
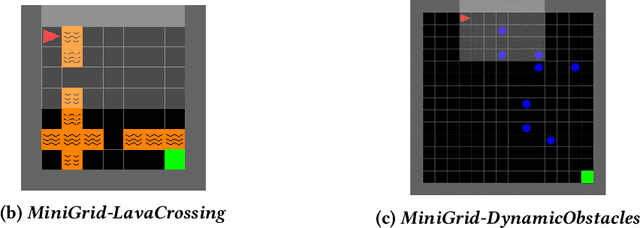
Policy robustness in Reinforcement Learning (RL) may not be desirable at any price; the alterations caused by robustness requirements from otherwise optimal policies should be explainable and quantifiable. Policy gradient algorithms that have strong convergence guarantees are usually modified to obtain robust policies in ways that do not preserve algorithm guarantees, which defeats the purpose of formal robustness requirements. In this work we study a notion of robustness in partially observable MDPs where state observations are perturbed by a noise-induced stochastic kernel. We characterise the set of policies that are maximally robust by analysing how the policies are altered by this kernel. We then establish a connection between such robust policies and certain properties of the noise kernel, as well as with structural properties of the underlying MDPs, constructing sufficient conditions for policy robustness. We use these notions to propose a robustness-inducing scheme, applicable to any policy gradient algorithm, to formally trade off the reward achieved by a policy with its robustness level through lexicographic optimisation, which preserves convergence properties of the original algorithm. We test the the proposed approach through numerical experiments on safety-critical RL environments, and show how the proposed method helps achieve high robustness when state errors are introduced in the policy roll-out.