Gradient Estimation with Discrete Stein Operators

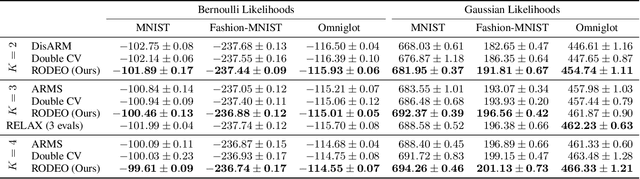
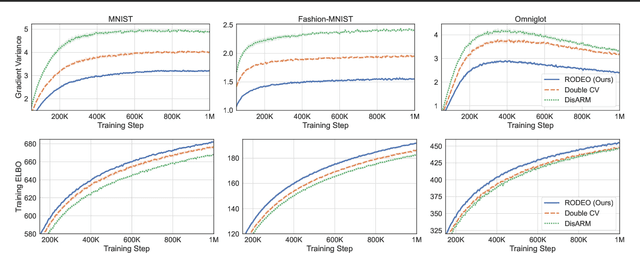
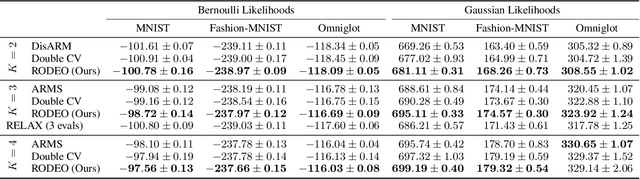
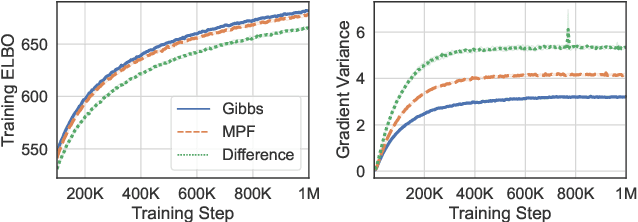
Gradient estimation -- approximating the gradient of an expectation with respect to the parameters of a distribution -- is central to the solution of many machine learning problems. However, when the distribution is discrete, most common gradient estimators suffer from excessive variance. To improve the quality of gradient estimation, we introduce a variance reduction technique based on Stein operators for discrete distributions. We then use this technique to build flexible control variates for the REINFORCE leave-one-out estimator. Our control variates can be adapted online to minimize the variance and do not require extra evaluations of the target function. In benchmark generative modeling tasks such as training binary variational autoencoders, our gradient estimator achieves substantially lower variance than state-of-the-art estimators with the same number of function evaluations.

Bounding Wasserstein distance with couplings

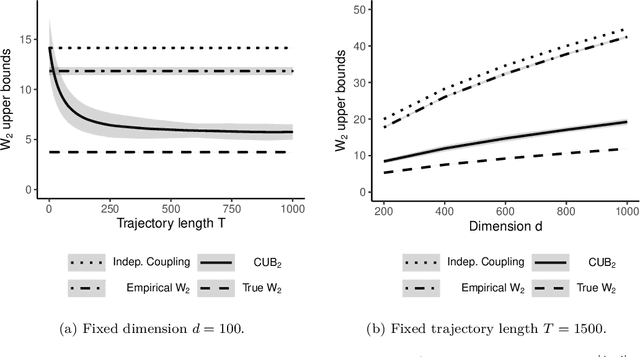
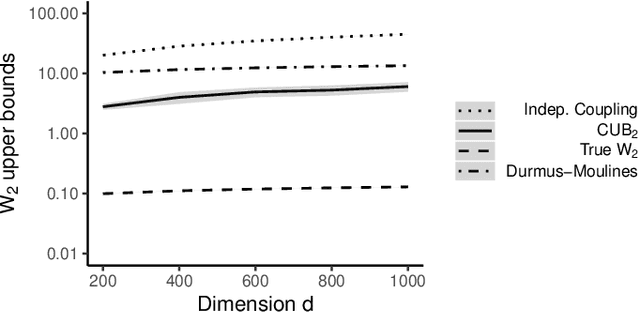
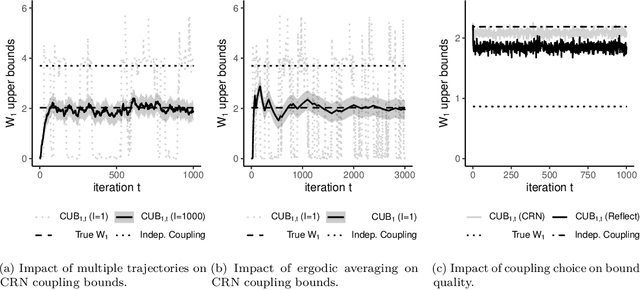
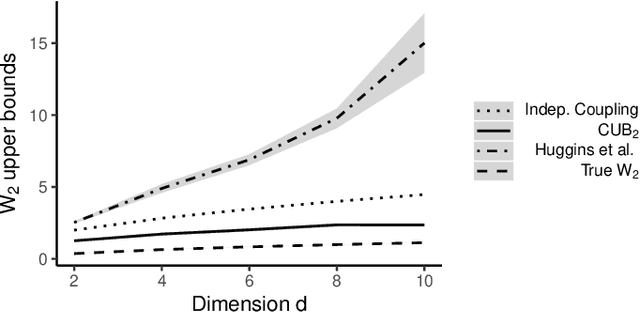
Markov chain Monte Carlo (MCMC) provides asymptotically consistent estimates of intractable posterior expectations as the number of iterations tends to infinity. However, in large data applications, MCMC can be computationally expensive per iteration. This has catalyzed interest in sampling methods such as approximate MCMC, which trade off asymptotic consistency for improved computational speed. In this article, we propose estimators based on couplings of Markov chains to assess the quality of such asymptotically biased sampling methods. The estimators give empirical upper bounds of the Wassertein distance between the limiting distribution of the asymptotically biased sampling method and the original target distribution of interest. We establish theoretical guarantees for our upper bounds and show that our estimators can remain effective in high dimensions. We apply our quality measures to stochastic gradient MCMC, variational Bayes, and Laplace approximations for tall data and to approximate MCMC for Bayesian logistic regression in 4500 dimensions and Bayesian linear regression in 50000 dimensions.

Distribution Compression in Near-linear Time

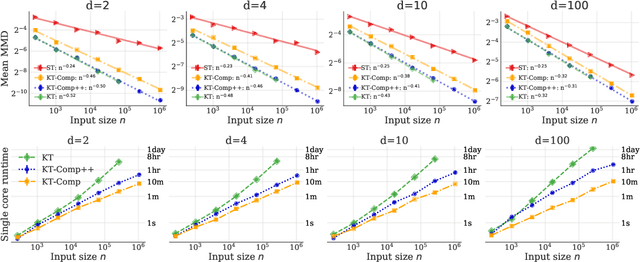
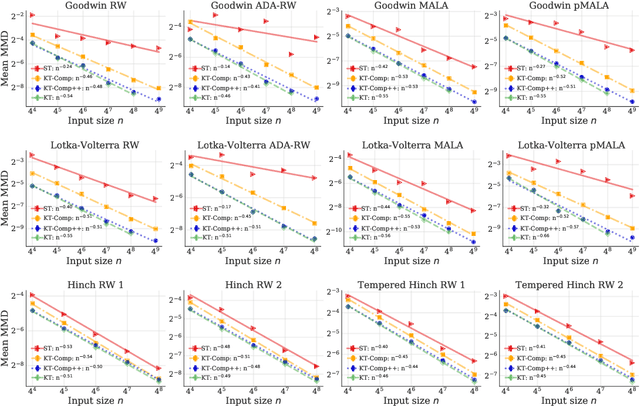
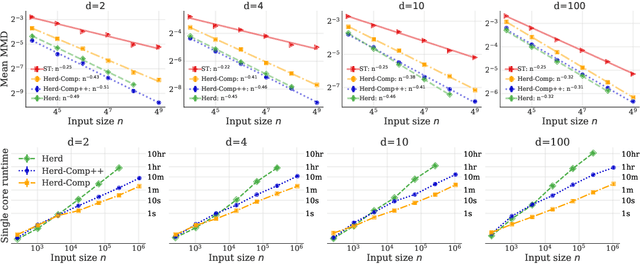
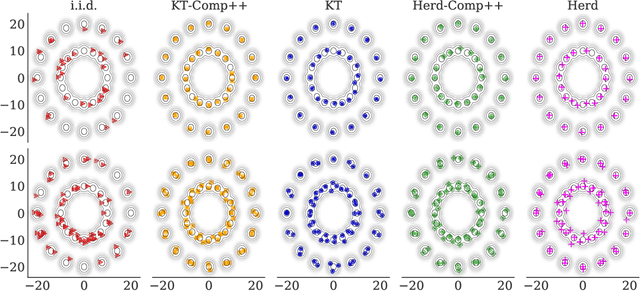
In distribution compression, one aims to accurately summarize a probability distribution $\mathbb{P}$ using a small number of representative points. Near-optimal thinning procedures achieve this goal by sampling $n$ points from a Markov chain and identifying $\sqrt{n}$ points with $\widetilde{\mathcal{O}}(1/\sqrt{n})$ discrepancy to $\mathbb{P}$. Unfortunately, these algorithms suffer from quadratic or super-quadratic runtime in the sample size $n$. To address this deficiency, we introduce Compress++, a simple meta-procedure for speeding up any thinning algorithm while suffering at most a factor of $4$ in error. When combined with the quadratic-time kernel halving and kernel thinning algorithms of Dwivedi and Mackey (2021), Compress++ delivers $\sqrt{n}$ points with $\mathcal{O}(\sqrt{\log n/n})$ integration error and better-than-Monte-Carlo maximum mean discrepancy in $\mathcal{O}(n \log^3 n)$ time and $\mathcal{O}( \sqrt{n} \log^2 n )$ space. Moreover, Compress++ enjoys the same near-linear runtime given any quadratic-time input and reduces the runtime of super-quadratic algorithms by a square-root factor. In our benchmarks with high-dimensional Monte Carlo samples and Markov chains targeting challenging differential equation posteriors, Compress++ matches or nearly matches the accuracy of its input algorithm in orders of magnitude less time.

Generalized Kernel Thinning

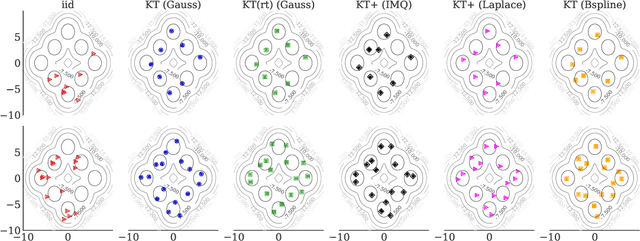
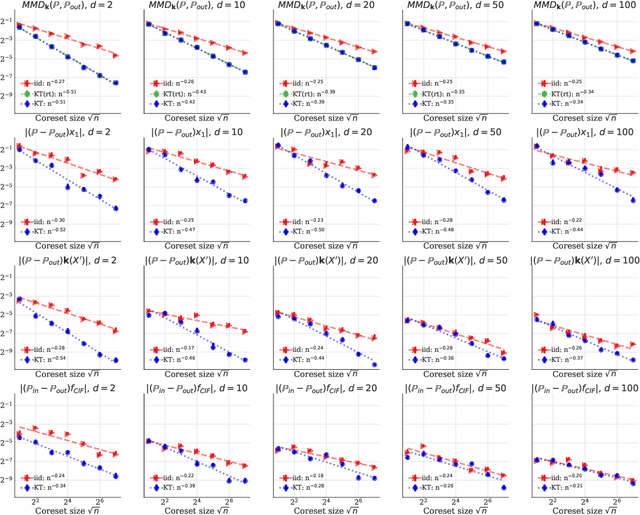
The kernel thinning (KT) algorithm of Dwivedi and Mackey (2021) compresses a probability distribution more effectively than independent sampling by targeting a reproducing kernel Hilbert space (RKHS) and leveraging a less smooth square-root kernel. Here we provide four improvements. First, we show that KT applied directly to the target RKHS yields tighter, dimension-free guarantees for any kernel, any distribution, and any fixed function in the RKHS. Second, we show that, for analytic kernels like Gaussian, inverse multiquadric, and sinc, target KT admits maximum mean discrepancy (MMD) guarantees comparable to or better than those of square-root KT without making explicit use of a square-root kernel. Third, we prove that KT with a fractional power kernel yields better-than-Monte-Carlo MMD guarantees for non-smooth kernels, like Laplace and Mat\'ern, that do not have square-roots. Fourth, we establish that KT applied to a sum of the target and power kernels (a procedure we call KT+) simultaneously inherits the improved MMD guarantees of power KT and the tighter individual function guarantees of target KT. In our experiments with target KT and KT+, we witness significant improvements in integration error even in $100$ dimensions and when compressing challenging differential equation posteriors.

Learned Benchmarks for Subseasonal Forecasting

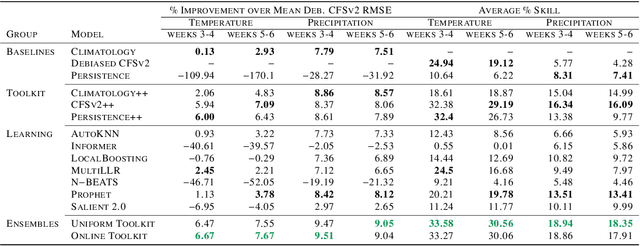
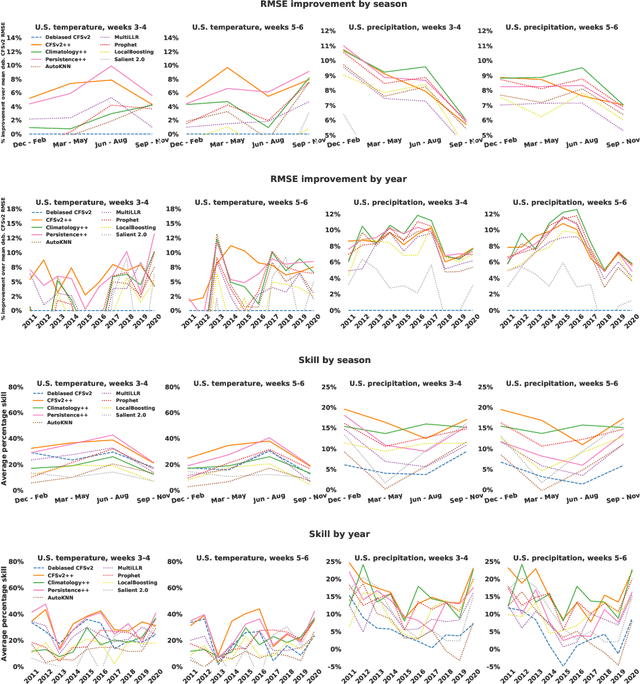
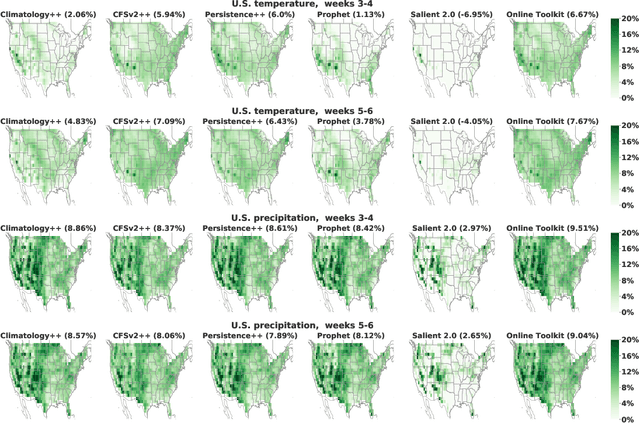
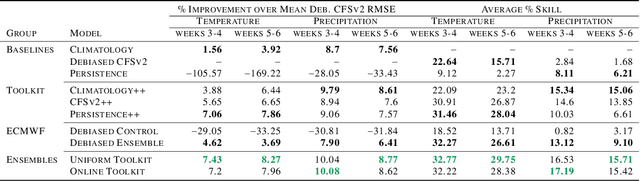
We develop a subseasonal forecasting toolkit of simple learned benchmark models that outperform both operational practice and state-of-the-art machine learning and deep learning methods. Our new models include (a) Climatology++, an adaptive alternative to climatology that, for precipitation, is 9% more accurate and 250% more skillful than the United States operational Climate Forecasting System (CFSv2); (b) CFSv2++, a learned CFSv2 correction that improves temperature and precipitation accuracy by 7-8% and skill by 50-275%; and (c) Persistence++, an augmented persistence model that combines CFSv2 forecasts with lagged measurements to improve temperature and precipitation accuracy by 6-9% and skill by 40-130%. Across the contiguous U.S., our Climatology++, CFSv2++, and Persistence++ toolkit consistently outperforms standard meteorological baselines, state-of-the-art machine and deep learning methods, and the European Centre for Medium-Range Weather Forecasts ensemble. Overall, we find that augmenting traditional forecasting approaches with learned enhancements yields an effective and computationally inexpensive strategy for building the next generation of subseasonal forecasting benchmarks.

Social Norm Bias: Residual Harms of Fairness-Aware Algorithms

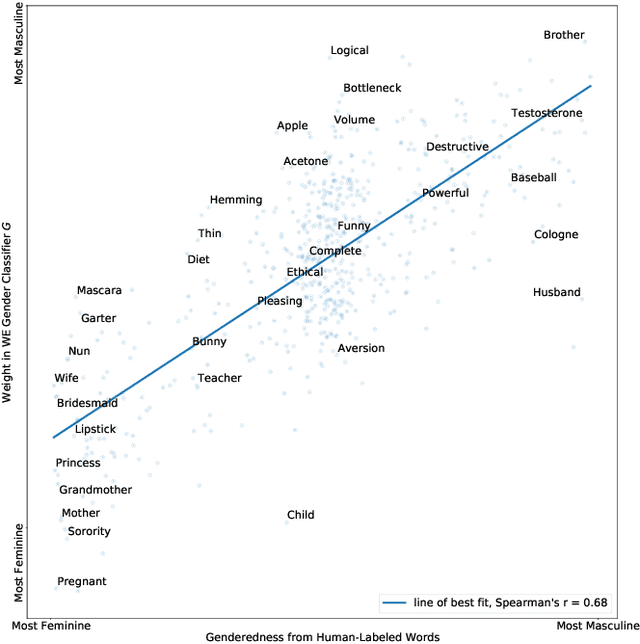
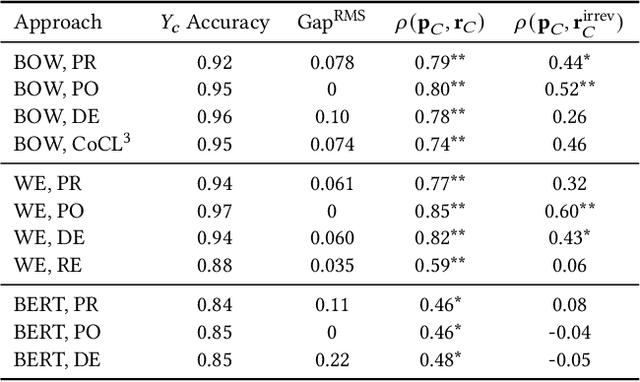
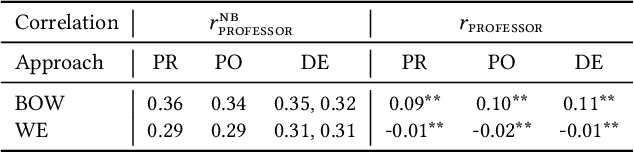
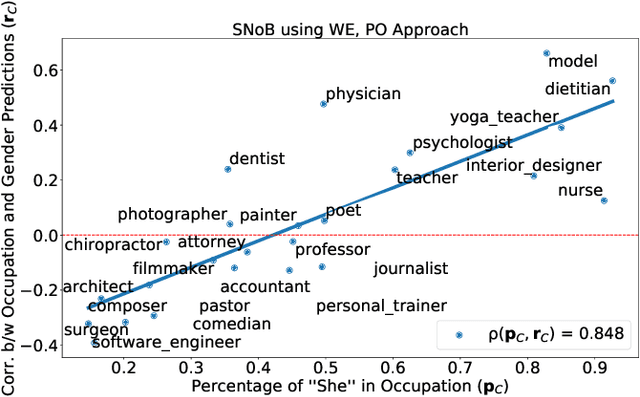
Many modern learning algorithms mitigate bias by enforcing fairness across coarsely-defined groups related to a sensitive attribute like gender or race. However, the same algorithms seldom account for the within-group biases that arise due to the heterogeneity of group members. In this work, we characterize Social Norm Bias (SNoB), a subtle but consequential type of discrimination that may be exhibited by automated decision-making systems, even when these systems achieve group fairness objectives. We study this issue through the lens of gender bias in occupation classification from biographies. We quantify SNoB by measuring how an algorithm's predictions are associated with conformity to gender norms, which is measured using a machine learning approach. This framework reveals that for classification tasks related to male-dominated occupations, fairness-aware classifiers favor biographies written in ways that align with masculine gender norms. We compare SNoB across fairness intervention techniques and show that post-processing interventions do not mitigate this type of bias at all.

Near-optimal inference in adaptive linear regression

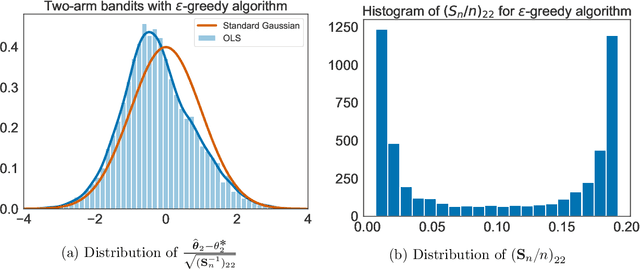
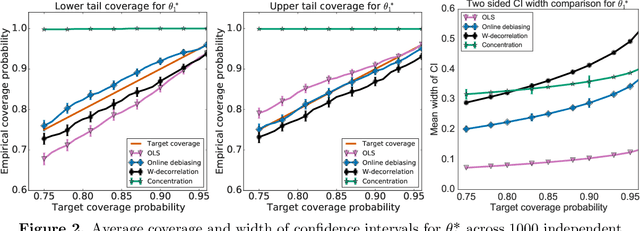
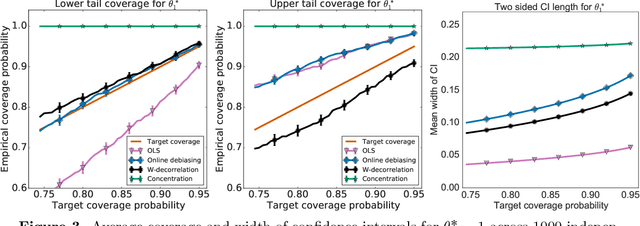
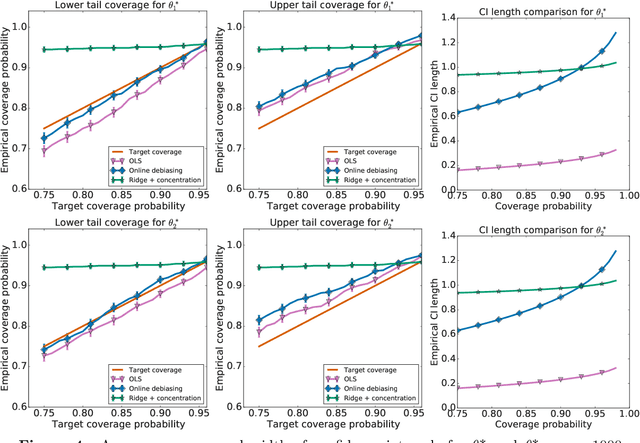
When data is collected in an adaptive manner, even simple methods like ordinary least squares can exhibit non-normal asymptotic behavior. As an undesirable consequence, hypothesis tests and confidence intervals based on asymptotic normality can lead to erroneous results. We propose an online debiasing estimator to correct these distributional anomalies in least squares estimation. Our proposed method takes advantage of the covariance structure present in the dataset and provides sharper estimates in directions for which more information has accrued. We establish an asymptotic normality property for our proposed online debiasing estimator under mild conditions on the data collection process, and provide asymptotically exact confidence intervals. We additionally prove a minimax lower bound for the adaptive linear regression problem, thereby providing a baseline by which to compare estimators. There are various conditions under which our proposed estimator achieves the minimax lower bound up to logarithmic factors. We demonstrate the usefulness of our theory via applications to multi-armed bandit, autoregressive time series estimation, and active learning with exploration.

Online Learning with Optimism and Delay

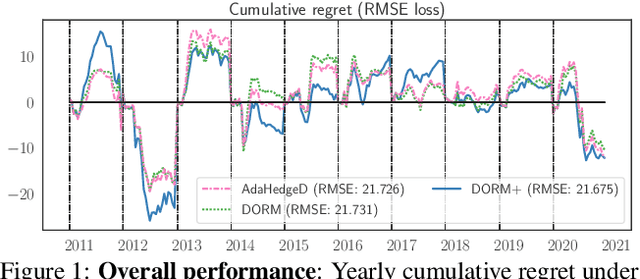
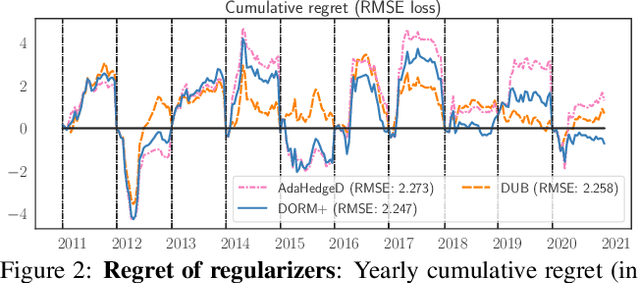
Inspired by the demands of real-time climate and weather forecasting, we develop optimistic online learning algorithms that require no parameter tuning and have optimal regret guarantees under delayed feedback. Our algorithms -- DORM, DORM+, and AdaHedgeD -- arise from a novel reduction of delayed online learning to optimistic online learning that reveals how optimistic hints can mitigate the regret penalty caused by delay. We pair this delay-as-optimism perspective with a new analysis of optimistic learning that exposes its robustness to hinting errors and a new meta-algorithm for learning effective hinting strategies in the presence of delay. We conclude by benchmarking our algorithms on four subseasonal climate forecasting tasks, demonstrating low regret relative to state-of-the-art forecasting models.

Sampling with Mirrored Stein Operators

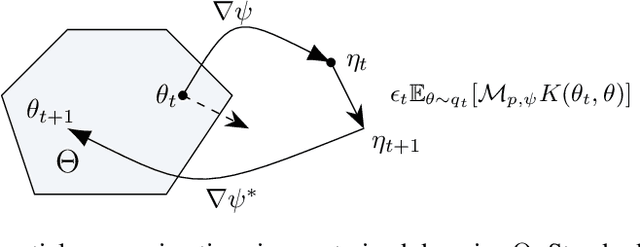
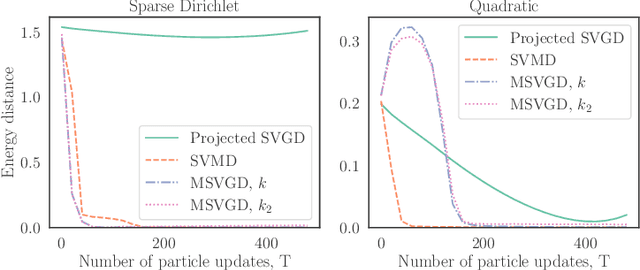
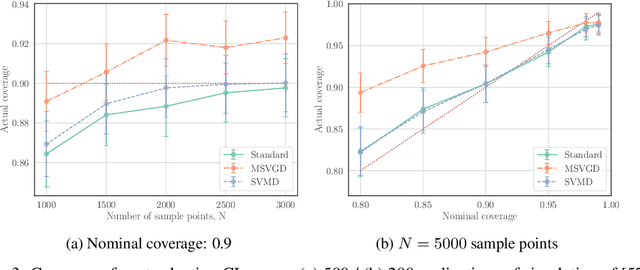
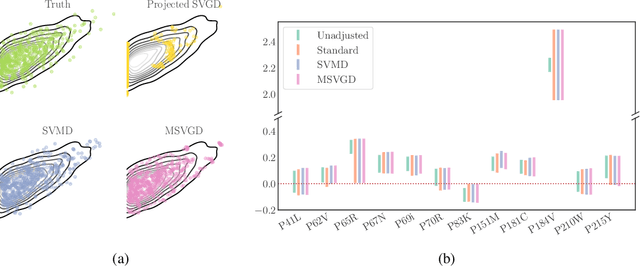
We introduce a new family of particle evolution samplers suitable for constrained domains and non-Euclidean geometries. Stein Variational Mirror Descent and Mirrored Stein Variational Gradient Descent minimize the Kullback-Leibler (KL) divergence to constrained target distributions by evolving particles in a dual space defined by a mirror map. Stein Variational Natural Gradient exploits non-Euclidean geometry to more efficiently minimize the KL divergence to unconstrained targets. We derive these samplers from a new class of mirrored Stein operators and adaptive kernels developed in this work. We demonstrate that these new samplers yield accurate approximations to distributions on the simplex, deliver valid confidence intervals in post-selection inference, and converge more rapidly than prior methods in large-scale unconstrained posterior inference. Finally, we establish the convergence of our new procedures under verifiable conditions on the target distribution.

Kernel Thinning

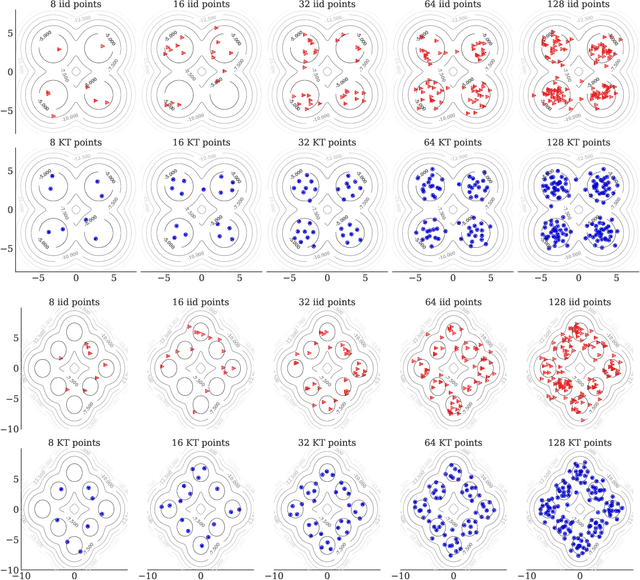
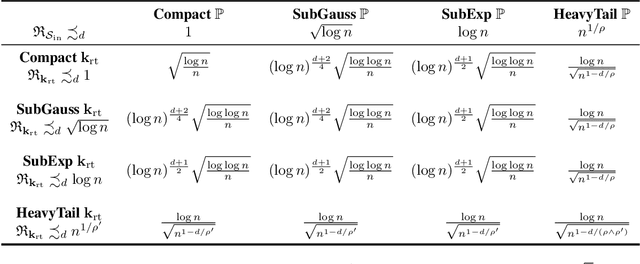
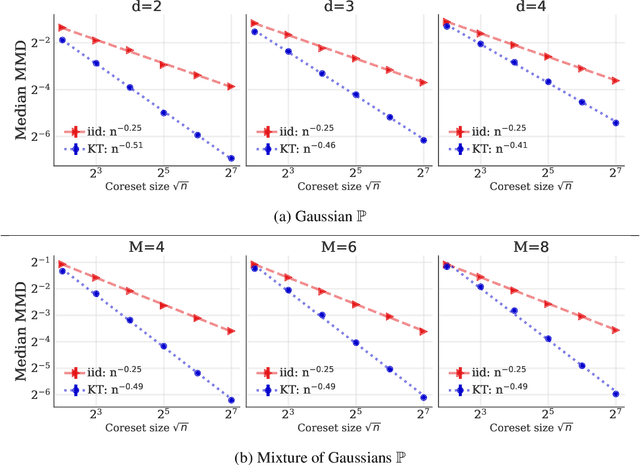
We introduce kernel thinning, a new procedure for compressing a distribution $\mathbb{P}$ more effectively than i.i.d. sampling or standard thinning. Given a suitable reproducing kernel $\mathbf{k}$ and $\mathcal{O}(n^2)$ time, kernel thinning compresses an $n$-point approximation to $\mathbb{P}$ into a $\sqrt{n}$-point approximation with comparable worst-case integration error in the associated reproducing kernel Hilbert space. With high probability, the maximum discrepancy in integration error is $\mathcal{O}_d(n^{-\frac{1}{2}}\sqrt{\log n})$ for compactly supported $\mathbb{P}$ and $\mathcal{O}_d(n^{-\frac{1}{2}} \sqrt{(\log n)^{d+1}\log\log n})$ for sub-exponential $\mathbb{P}$ on $\mathbb{R}^d$. In contrast, an equal-sized i.i.d. sample from $\mathbb{P}$ suffers $\Omega(n^{-\frac14})$ integration error. Our sub-exponential guarantees resemble the classical quasi-Monte Carlo error rates for uniform $\mathbb{P}$ on $[0,1]^d$ but apply to general distributions on $\mathbb{R}^d$ and a wide range of common kernels. We use our results to derive explicit non-asymptotic maximum mean discrepancy bounds for Gaussian, Mat\'ern, and B-spline kernels and present two vignettes illustrating the practical benefits of kernel thinning over i.i.d. sampling and standard Markov chain Monte Carlo thinning.