SHAP@k:Efficient and Probably Approximately Correct (PAC) Identification of Top-k Features

The SHAP framework provides a principled method to explain the predictions of a model by computing feature importance. Motivated by applications in finance, we introduce the Top-k Identification Problem (TkIP), where the objective is to identify the k features with the highest SHAP values. While any method to compute SHAP values with uncertainty estimates (such as KernelSHAP and SamplingSHAP) can be trivially adapted to solve TkIP, doing so is highly sample inefficient. The goal of our work is to improve the sample efficiency of existing methods in the context of solving TkIP. Our key insight is that TkIP can be framed as an Explore-m problem--a well-studied problem related to multi-armed bandits (MAB). This connection enables us to improve sample efficiency by leveraging two techniques from the MAB literature: (1) a better stopping-condition (to stop sampling) that identifies when PAC (Probably Approximately Correct) guarantees have been met and (2) a greedy sampling scheme that judiciously allocates samples between different features. By adopting these methods we develop KernelSHAP@k and SamplingSHAP@k to efficiently solve TkIP, offering an average improvement of $5\times$ in sample-efficiency and runtime across most common credit related datasets.

Comparing Apples to Oranges: Learning Similarity Functions for Data Produced by Different Distributions

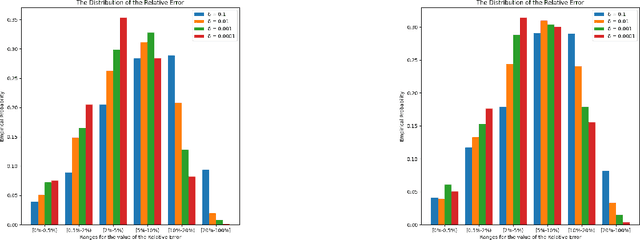
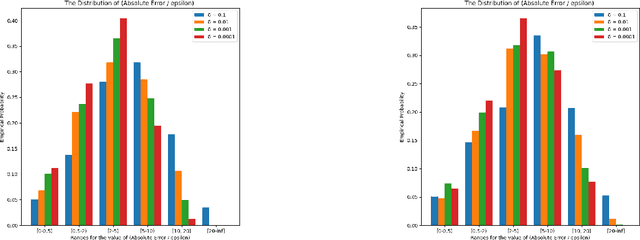
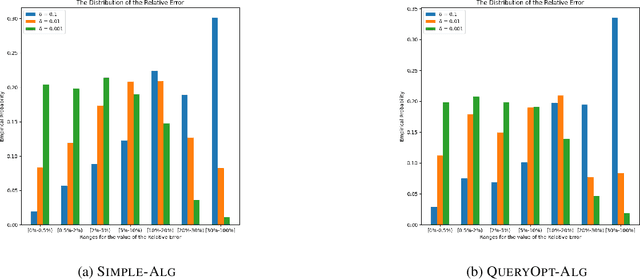
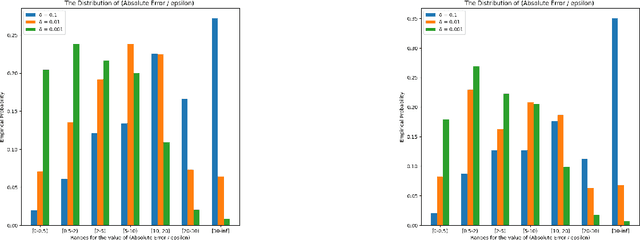
Similarity functions measure how comparable pairs of elements are, and play a key role in a wide variety of applications, e.g., Clustering problems and considerations of Individual Fairness. However, access to an accurate similarity function should not always be considered guaranteed. Specifically, when the elements to be compared are produced by different distributions, or in other words belong to different ``demographic'' groups, knowledge of their true similarity might be very difficult to obtain. In this work, we present a sampling framework that learns these across-groups similarity functions, using only a limited amount of experts' feedback. We show analytical results with rigorous bounds, and empirically validate our algorithms via a large suite of experiments.

Controlling Epidemic Spread using Probabilistic Diffusion Models on Networks

The spread of an epidemic is often modeled by an SIR random process on a social network graph. The MinINF problem for optimal social distancing involves minimizing the expected number of infections, when we are allowed to break at most $B$ edges; similarly the MinINFNode problem involves removing at most $B$ vertices. These are fundamental problems in epidemiology and network science. While a number of heuristics have been considered, the complexity of these problems remains generally open. In this paper, we present two bicriteria approximation algorithms for MinINF, which give the first non-trivial approximations for this problem. The first is based on the cut sparsification result of Karger \cite{karger:mathor99}, and works when the transmission probabilities are not too small. The second is a Sample Average Approximation (SAA) based algorithm, which we analyze for the Chung-Lu random graph model. We also extend some of our results to tackle the MinINFNode problem.

Deploying Vaccine Distribution Sites for Improved Accessibility and Equity to Support Pandemic Response

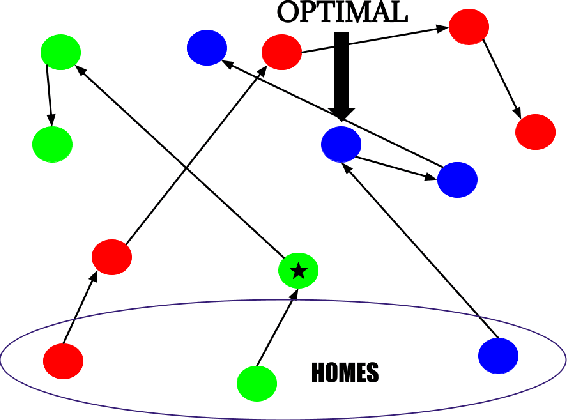
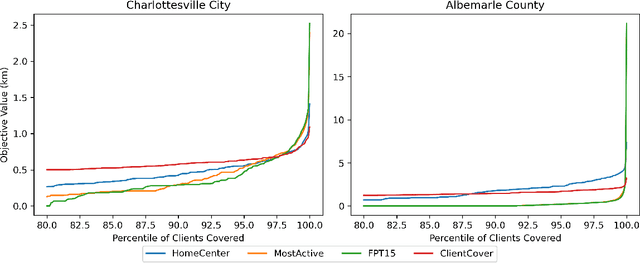
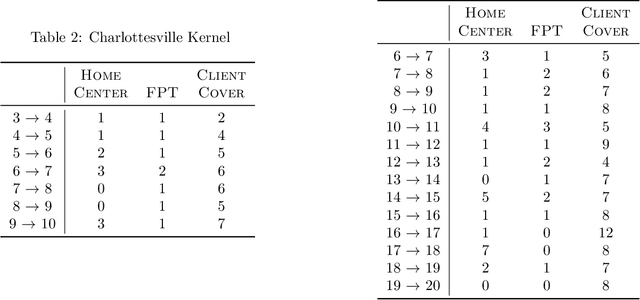
In response to COVID-19, many countries have mandated social distancing and banned large group gatherings in order to slow down the spread of SARS-CoV-2. These social interventions along with vaccines remain the best way forward to reduce the spread of SARS CoV-2. In order to increase vaccine accessibility, states such as Virginia have deployed mobile vaccination centers to distribute vaccines across the state. When choosing where to place these sites, there are two important factors to take into account: accessibility and equity. We formulate a combinatorial problem that captures these factors and then develop efficient algorithms with theoretical guarantees on both of these aspects. Furthermore, we study the inherent hardness of the problem, and demonstrate strong impossibility results. Finally, we run computational experiments on real-world data to show the efficacy of our methods.

Fair Disaster Containment via Graph-Cut Problems

Graph cut problems form a fundamental problem type in combinatorial optimization, and are a central object of study in both theory and practice. In addition, the study of fairness in Algorithmic Design and Machine Learning has recently received significant attention, with many different notions proposed and analyzed in a variety of contexts. In this paper we initiate the study of fairness for graph cut problems by giving the first fair definitions for them, and subsequently we demonstrate appropriate algorithmic techniques that yield a rigorous theoretical analysis. Specifically, we incorporate two different definitions of fairness, namely demographic and probabilistic individual fairness, in a particular cut problem modeling disaster containment scenarios. Our results include a variety of approximation algorithms with provable theoretical guarantees.

A New Notion of Individually Fair Clustering: $α$-Equitable $k$-Center

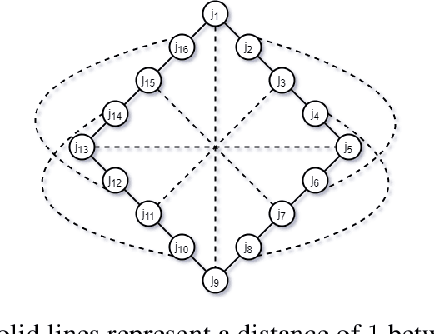
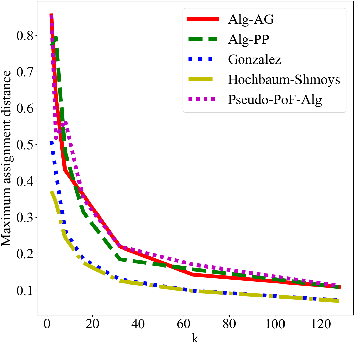
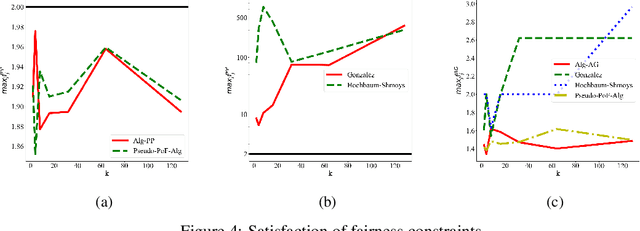
Clustering is a fundamental problem in unsupervised machine learning, and fair variants of it have recently received significant attention. In this work we introduce a novel definition of fairness for clustering problems. Specifically, in our model each point $j$ has a set of other points $\mathcal{S}_j$ that it perceives as similar to itself, and it feels that it is fairly treated, if the quality of service it receives in the solution is $\alpha$-close to that of the points in $\mathcal{S}_j$. We begin our study by answering questions regarding the structure of the problem, namely for what values of $\alpha$ the problem is well-defined, and what the behavior of the Price of Fairness (PoF) for it is. For the well-defined region of $\alpha$, we provide efficient and easily implementable approximation algorithms for the $k$-center objective, which in certain cases also enjoy bounded PoF guarantees. We finally complement our analysis by an extensive suite of experiments that validates the effectiveness of our theoretical results.

Fairness, Semi-Supervised Learning, and More: A General Framework for Clustering with Stochastic Pairwise Constraints

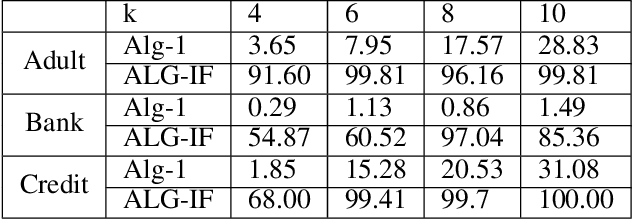
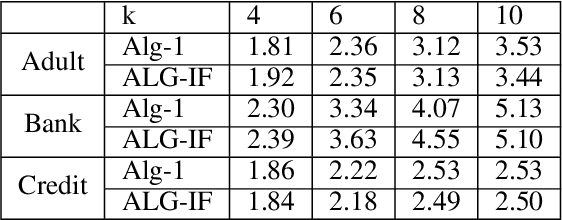
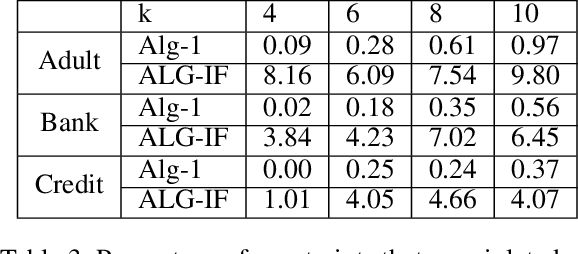
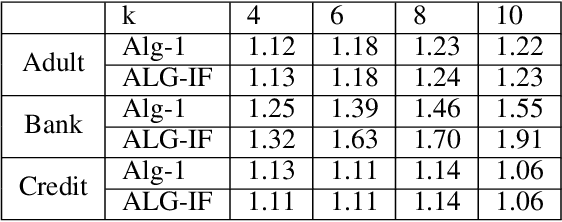
Metric clustering is fundamental in areas ranging from Combinatorial Optimization and Data Mining, to Machine Learning and Operations Research. However, in a variety of situations we may have additional requirements or knowledge, distinct from the underlying metric, regarding which pairs of points should be clustered together. To capture and analyze such scenarios, we introduce a novel family of \emph{stochastic pairwise constraints}, which we incorporate into several essential clustering objectives (radius/median/means). Moreover, we demonstrate that these constraints can succinctly model an intriguing collection of applications, including among others \emph{Individual Fairness} in clustering and \emph{Must-link} constraints in semi-supervised learning. Our main result consists of a general framework that yields approximation algorithms with provable guarantees for important clustering objectives, while at the same time producing solutions that respect the stochastic pairwise constraints. Furthermore, for certain objectives we devise improved results in the case of Must-link constraints, which are also the best possible from a theoretical perspective. Finally, we present experimental evidence that validates the effectiveness of our algorithms.

A Pairwise Fair and Community-preserving Approach to k-Center Clustering

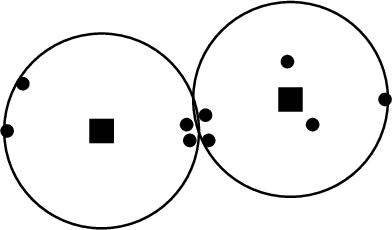
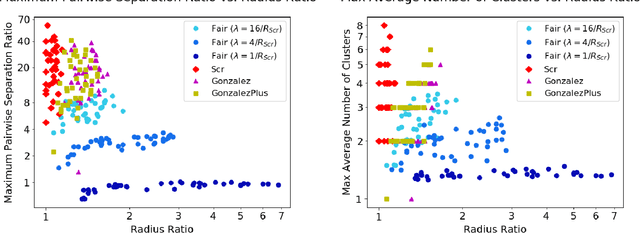
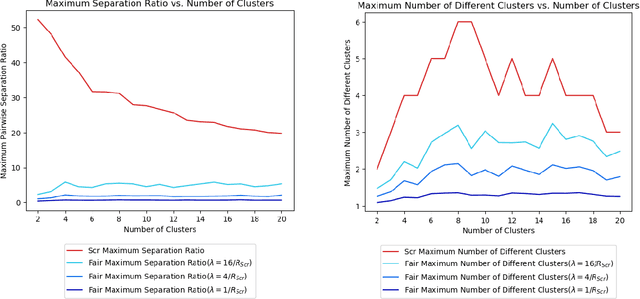
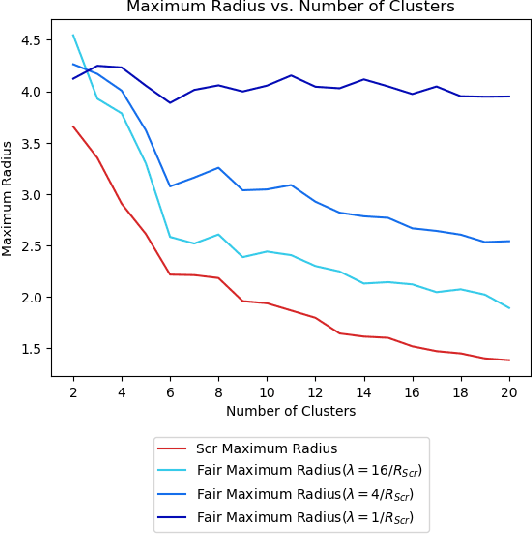
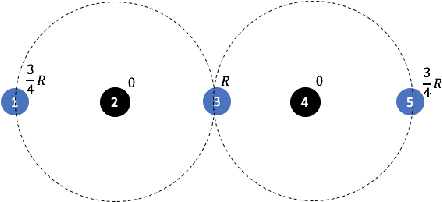
Clustering is a foundational problem in machine learning with numerous applications. As machine learning increases in ubiquity as a backend for automated systems, concerns about fairness arise. Much of the current literature on fairness deals with discrimination against protected classes in supervised learning (group fairness). We define a different notion of fair clustering wherein the probability that two points (or a community of points) become separated is bounded by an increasing function of their pairwise distance (or community diameter). We capture the situation where data points represent people who gain some benefit from being clustered together. Unfairness arises when certain points are deterministically separated, either arbitrarily or by someone who intends to harm them as in the case of gerrymandering election districts. In response, we formally define two new types of fairness in the clustering setting, pairwise fairness and community preservation. To explore the practicality of our fairness goals, we devise an approach for extending existing $k$-center algorithms to satisfy these fairness constraints. Analysis of this approach proves that reasonable approximations can be achieved while maintaining fairness. In experiments, we compare the effectiveness of our approach to classical $k$-center algorithms/heuristics and explore the tradeoff between optimal clustering and fairness.

Probabilistic Fair Clustering

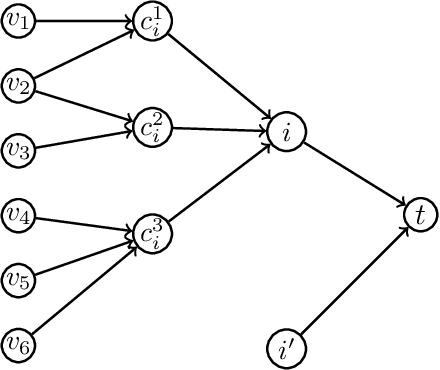
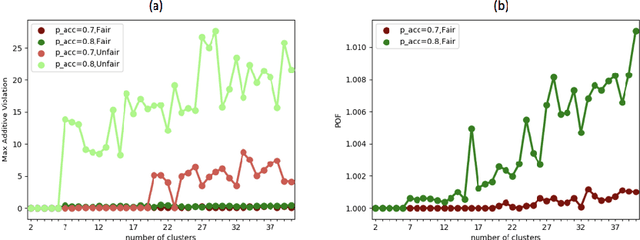
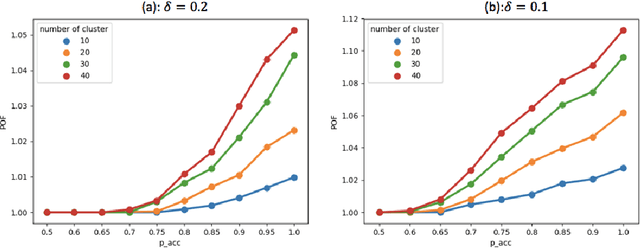
In clustering problems, a central decision-maker is given a complete metric graph over vertices and must provide a clustering of vertices that minimizes some objective function. In fair clustering problems, vertices are endowed with a color (e.g., membership in a group), and the features of a valid clustering might also include the representation of colors in that clustering. Prior work in fair clustering assumes complete knowledge of group membership. In this paper, we generalize prior work by assuming imperfect knowledge of group membership through probabilistic assignments. We present clustering algorithms in this more general setting with approximation ratio guarantees. We also address the problem of "metric membership", where different groups have a notion of order and distance. Experiments are conducted using our proposed algorithms as well as baselines to validate our approach and also surface nuanced concerns when group membership is not known deterministically.