Inverse-designed nanophotonic neural network accelerators for ultra-compact optical computing

Inverse-designed nanophotonic devices offer promising solutions for analog optical computation. High-density photonic integration is critical for scaling such architectures toward more complex computational tasks and large-scale applications. Here, we present an inverse-designed photonic neural network (PNN) accelerator on a high-index contrast material platform, enabling ultra-compact and energy-efficient optical computing. Our approach introduces a wave-based inverse-design method based on three dimensional finite-difference time-domain (3D-FDTD) simulations, exploiting the linearity of Maxwell's equations to reconstruct arbitrary spatial fields through optical coherence. By decoupling the forward-pass process into linearly separable simulations, our approach is highly amenable to computational parallelism, making it particularly well suited for acceleration using graphics processing units (GPUs) and other parallel computing platforms, thereby enhancing scalability across large problem domains. We fabricate and experimentally validate two inverse-designed PNN accelerators on the silicon-on-insulator platform, achieving on-chip MNIST and MedNIST classification accuracies of 89% and 90% respectively, within ultra-compact footprints of just 20 $\times$ 20 $\mu$m$^{2}$ and 30 $\times$ 20 $\mu$m$^{2}$. Our results establish a scalable and energy-efficient platform for analog photonic computing, effectively bridging inverse nanophotonic design with high-performance optical information processing.

Deploying Vaccine Distribution Sites for Improved Accessibility and Equity to Support Pandemic Response

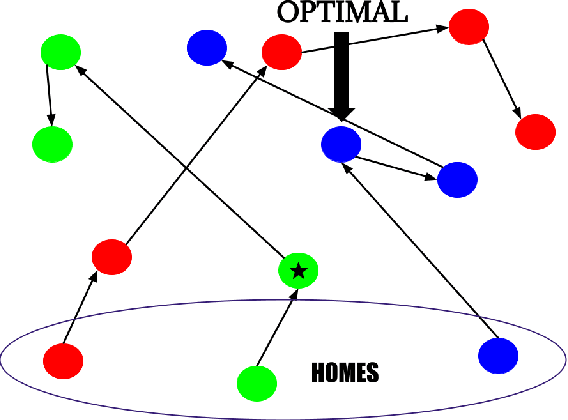
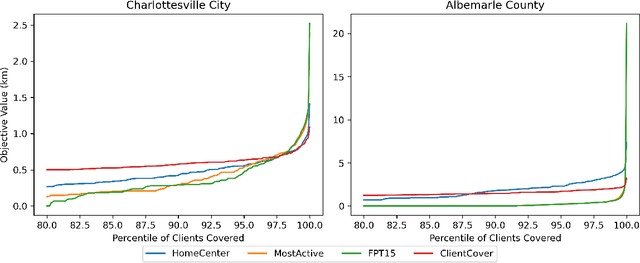
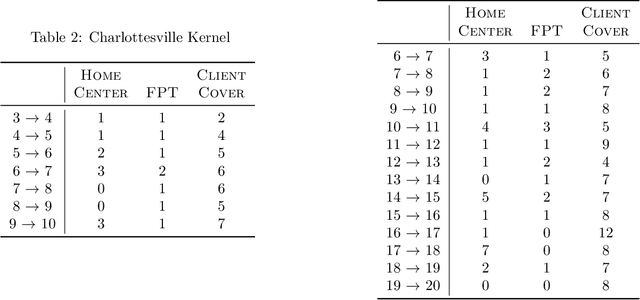
In response to COVID-19, many countries have mandated social distancing and banned large group gatherings in order to slow down the spread of SARS-CoV-2. These social interventions along with vaccines remain the best way forward to reduce the spread of SARS CoV-2. In order to increase vaccine accessibility, states such as Virginia have deployed mobile vaccination centers to distribute vaccines across the state. When choosing where to place these sites, there are two important factors to take into account: accessibility and equity. We formulate a combinatorial problem that captures these factors and then develop efficient algorithms with theoretical guarantees on both of these aspects. Furthermore, we study the inherent hardness of the problem, and demonstrate strong impossibility results. Finally, we run computational experiments on real-world data to show the efficacy of our methods.